Правила сложения перемещений и скоростей
п.1. Правило сложения перемещений при прямолинейном движении
Рассмотрим движение катера по реке.
Можно говорить о движении катера как относительно реки, так и относительно берега.
При этом сама река также движется относительно берега.
Как было показано в §5 данного справочника, для описания движения необходимо указать тело отсчета и ввести связанную с ним систему отсчета.
Введем две системы отсчета.
Берег неподвижен. Назовем систему отсчета, связанную с берегом, неподвижной системой отсчета (НСО). Перемещение тела в НСО назовем абсолютным перемещением, \(\overrightarrow{r_a}.\)
Река подвижна. Назовем систему отсчета, связанную с рекой, подвижной системой отсчета (ПСО). Перемещение тела в ПСО назовем относительным перемещением, \(\overrightarrow{r_o}.\)
Перемещение реки относительно берега – это перемещение подвижной системы отсчета относительно неподвижной. Перемещение ПСО относительно НСО назовем переносным перемещением, \(\overrightarrow{r_п}.\)
Абсолютное перемещение равно векторной сумме относительного и переносного перемещений: $$ \overrightarrow{r_a}=\overrightarrow{r_o}+ \overrightarrow{r_п} $$
Чтобы найти сумму двух векторов, нужно от конца первого вектора отложить второй вектор (см. §6 данного справочника).
При прямолинейном движении все перемещения направлены вдоль одной прямой. В этом случае сумму векторов найти проще.
Пример: правило сложения перемещений при движении катера по реке
Пусть катер плывет по течению реки.
В этом случае векторы \(\overrightarrow{r_o}\) и \(\overrightarrow{r_п}\) направлены в одну сторону, и модуль абсолютного перемещения равен сумме модулей векторов-слагаемых:

$$ |\overrightarrow{r_a}|=|\overrightarrow{r_o}|+ |\overrightarrow{r_п}| $$
Теперь пусть катер плывет против течения.
В этом случае векторы \(\overrightarrow{r_o}\) и \(\overrightarrow{r_п}\) направлены в противоположные стороны, и модуль абсолютного перемещения равен разности модуля большего и модуля меньшего вектора:

$$ |\overrightarrow{r_a}|=|\overrightarrow{r_o}|- |\overrightarrow{r_п}| $$
п.2. Правило сложения скоростей при прямолинейном движении
Напомним, что:
Тогда из закона сложения перемещений получаем: $$ \overrightarrow{r_a}=\overrightarrow{r_o} +\overrightarrow{r_п} \Rightarrow \frac{\overrightarrow{r_a}}{t}=\frac{\overrightarrow{r_o}}{t} +\frac{\overrightarrow{r_п}}{t}\Rightarrow \overrightarrow{v_a}=\overrightarrow{v_o} +\overrightarrow{v_п} $$
Абсолютная скорость равна векторной сумме относительной и переносной скоростей: $$ \overrightarrow{v_a}=\overrightarrow{v_o} +\overrightarrow{v_п} $$
Если при описании движения выбрать направление координатной оси ОХ, то можно ввести проекции скоростей \(v_x\) (см. §8 данного справочника) и получить еще одно очень полезное при решении задач правило сложения:
Проекция абсолютной скорости на координатную ось ОХ равна сумме проекций относительной и переносной скоростей: $$ v_{ax}=v_{ox}+v_{пx} $$
п.3. Абсолютная скорость при движении катера по реке
Пусть собственная скорость катера (скорость относительно реки) равна \(v\), скорость течения (переносная скорость) равна \(u\).
Направим ось ОХ в направлении скорости катера, тогда её проекция будет положительной: \(v_{ox}=v\). Если катер плывет по течению, скорость течения также направлена по ОХ и её проекция положительна: \(v_{пx}=u\). Проекция абсолютной скорости равна сумме: $$ v_{ax}=v_{ox}+v_{пx}=v+u $$
Если катер плывет против течения, при сохранении направления оси OX скорость течения направлена противоположно и её проекция отрицательна: \(v_{пx}=-u\). Проекция абсолютной скорости равна разности $$ v_{ax}=v_{ox}+v_{пx}=v-u $$ Если \(v\gt u\), проекция абсолютной скорости положительна, \(v_{ax}\gt 0\), катер поднимается вверх по реке.
При недостаточной скорости катера \(v\lt u\), проекция абсолютной скорости отрицательна, \(v_{ax}\lt 0\). Катер не сможет подниматься вверх по реке, его будет сносить вниз.
При описании прямолинейного движения выбор направления оси ОХ, определение знаков проекций скоростей и перемещений важны для правильного хода решения задачи и объяснения полученных результатов.
Всегда помните: скорость и перемещение – это вектора, у которых есть не только величина, но и направление.
п.4. Задачи
Задача 1. По заданным векторам относительной и переносной скоростей найдите вектор абсолютной скорости. Какой путь пройдет тело в подвижной и неподвижной системе отсчета за 5 с?
a)
Вектор абсолютной скорости равен сумме векторов: \(\overrightarrow{v_a}=\overrightarrow{v_o} +\overrightarrow{v_п}\)
Находим сумму: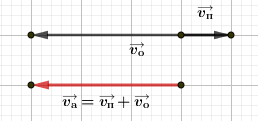
Пользуясь заданным масштабом, получаем:
\(\overrightarrow{v_o}=|\overrightarrow{v_o}|=4\ \text{м/с}\) - скорость тела в подвижной СО
\(\overrightarrow{v_a}=|\overrightarrow{v_a}|=3\ \text{м/с}\) - скорость тела в неподвижной СО
Путь тела в разных СО:
\(s_о=v_о t;\ \ s_о=4\cdot 5=20\ \text{м}\) - путь тела в подвижной СО
\(s_a=v_a t;\ \ s_a=3\cdot 5=15\ \text{м}\) - путь тела в неподвижной СО
Ответ: 20 м и 15 м
б) 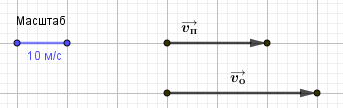
Вектор абсолютной скорости равен сумме векторов: \(\overrightarrow{v_a}=\overrightarrow{v_o} +\overrightarrow{v_п}\)
Находим сумму: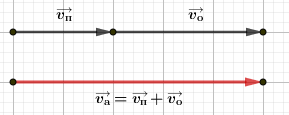
Пользуясь заданным масштабом, получаем:
\(\overrightarrow{v_o}=|\overrightarrow{v_o}|=30\ \text{м/с}\) - скорость тела в подвижной СО
\(\overrightarrow{v_a}=|\overrightarrow{v_a}|=50\ \text{м/с}\) - скорость тела в неподвижной СО
Путь тела в разных СО:
\(s_о=v_о t;\ \ s_о=30\cdot 5=150\ \text{м}\) - путь тела в подвижной СО
\(s_a=v_a t;\ \ s_a=50\cdot 5=250\ \text{м}\) - путь тела в неподвижной СО
Ответ: 150 м и 250 м
Задача 2. Между двумя катерами, которые движутся навстречу друг другу со скоростями 10 км/ч и 12 км/ч, летает альбатрос с постоянной скоростью 15 км/ч. Сколько километров он пролетит до момента встречи катеров, если первоначальное расстояние между ними равнялось 99 км.
Дано:
\(v_1=10\ \text{км/ч}\)
\(v_2=12\ \text{км/ч}\)
\(v=15\ \text{км/ч}\)
\(d=99\ \text{км}\)
_______________
\(s-?\)
Пусть первый катер – неподвижное тело отсчета. Тогда второй катер приближается к нему со скоростью, равной сумме скоростей \((v_1+v_2)\). Время, через которое катера встретятся: $$ t=\frac{d}{v_1+v_2} $$ За это время альбатрос пролетит расстояние: $$ s=vt=v\cdot\frac{d}{v_1+v_2}=\frac{v}{v_1+v_2}d $$ Подставляем: $$ s=\frac{15}{10+12}\cdot 99=67,5\ (\text{км}) $$ Ответ: 67,5 км
Задача 3. В подрывной технике используют бикфордов шнур, пламя по которому распространяется со скоростью 0,8 см/с. Какой длины шнур понадобится подрывнику, чтобы он успел отбежать на расстояние 300 м после того, как его подожжет?
Скорость бега равна 5 м/с.
Дано:
\(u=0,8\ \text{см/с}=0,008\ \text{м/с}\)
\(v=5\ \text{м/c}\)
\(s=300\ \text{м}\)
_______________
\(L-?\) 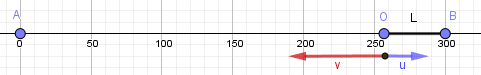
На чертеже объект, который нужно взорвать, находится в точке B. Подрывник находится в точке O и бежит в точку A, длина шнура L=OB, расстояние AB=s.
Скорости \(u\) и \(v\) направлены противоположно. Время, за которое шнур догорит и подрывник добежит, определяется суммой скоростей \((u+v)\): $$ t=\frac{s}{u+v} $$ Длина шнура определяется временем и скоростью сгорания: $$ L=tu=\frac{su}{u+v} $$ Подставляем: $$ L=\frac{300\cdot 0,008}{5+0,008}\approx 0,48\ (\text{м})=48\ (\text{см}) $$ Ответ: 48 см
Задача 4. Из городов A и B, расстояние между которыми d=9 км, одновременно навстречу друг другу выехало два велосипедиста. В направлении от A к B дует ветер со скоростью \(v_0\). Первый велосипедист проехал расстояние между городами за 30 минут, а второй – за 45 минут. Найдите скорость ветра \(v_0\) и скорость велосипедистов в безветренную погоду, если она у них одинакова.
Пусть \(v\) - скорость велосипедистов в тихую погоду.
Переведем время в часы: \begin{gather*} t_1=30\ \text{мин}=\frac{30}{60}\text{ч}=\frac12\text{ч}\\ t_2=45\ \text{мин}=\frac{45}{60}\text{ч}=\frac34\text{ч} \end{gather*} Составим таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й велосипедист, из А в Б |
\(v+v_0\) | \(\frac12\) | \(\frac12(v+v_0)\) |
| 2й велосипедист, из Б в А |
\(v-v_0\) | \(\frac34\) | \(\frac34(v-v_0)\) |
Расстояние: $$ d=\frac12(v+v_0)=\frac34(v-v_0)=9 $$ Получаем систему: $$ \begin{cases} \frac12(v+v_0)=9\\ \frac34(v-v_0)=9 \end{cases} \Rightarrow \begin{cases} v+v_0=9\cdot 2=18\\ v-v_0=9\cdot\frac43=12 \end{cases} \Rightarrow \begin{cases} 2v=18+12\\ 2v_0=18-12 \end{cases} \Rightarrow \begin{cases} v=\frac{30}{2}=15\\ v_0=\frac62=3 \end{cases} $$
Ответ:
Скорость ветра \(v_0=3\) км/ч
Скорость велосипедистов в тихую погоду \(v=15\) км/ч
Задача 5. Катер проходит расстояние между двумя пристанями по течению реки за 2 ч, а против течения – за 4 ч. За какое время от одной пристани к другой проплывет плот?
Пусть \(v\) - скорость катера относительно реки (относительная скорость), \(u\) - скорость реки относительно берега (переносная скорость).
Составим таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| Катер по течению | \(v+u\) | 2 | \(2(v+u)\) |
| Катер против течения | \(v-u\) | 4 | \(4(v-u)\) |
| Плот | \(u\) | \(t\) | \(s\) |
Расстояние во всех случаях одно и то же: $$ s=2(v+u)=4(v-u)\Rightarrow (v+u)=2(v-u)\Rightarrow u+2u=2v-v\Rightarrow 3u=v $$ Скорость катера в 3 раза больше скорости течения (скорости плота).
Тогда расстояние \(s=2(v+u)=2(3u+u)=8u\)
Время для плота: $$ t=\frac su=\frac{8u}{u}=8\ (\text{ч}) $$
Ответ: 8 ч
Задача 6*. Два космических корабля сближаются со скоростью \(v=8\cdot 10^3\) км/ч. С первого корабля на второй каждые \(\triangle t=20\) мин отправляют контейнеры с грузом со скоростью \(v_1=8\cdot 10^3\) км/ч относительно первого корабля. Сколько контейнеров получит командир второго корабля в течение часа после того, как подберёт первый контейнер?
Пусть первый корабль – неподвижное тело отсчета.
Тогда скорость второго корабля равна \(v\) и направлена к первому кораблю, скорость контейнеров равна \(v_1\) и направлена от первого корабля.
Второй корабль и контейнеры движутся навстречу друг другу, их скорости суммируются, т.е. второй корабль подбирает контейнеры со скоростью \(u=v+v_1=16\cdot 10^3\) км/ч.
Расстояние между контейнерами: \(s=v_1\cdot\triangle t=8\cdot 10^3\cdot\frac13=\frac83\cdot 10^3\) км.
Время подбора двух соседних контейнеров вторым кораблем: \(t=\frac su=\frac{\frac83\cdot 10^3}{16\cdot 10^3}=\frac16\ \text{ч}=10\ \text{мин}\)
Второй корабль подбирает контейнеры каждые 10 мин.
Значит, в течение часа второй корабль подберет еще \(N=\frac{60\ \text{мин}}{10\ \text{мин}}=6\) контейнеров.
Ответ: 6 контейнеров
Задача 7*. Автомобиль, движущийся со скоростью 72 км/ч, был пробит пулей, летевшей перпендикулярно его движению. Отверстие в дальней стенке оказалось смещено относительно отверстия в ближней стенке на 4 см. Ширина салона 1,5 м. Считая, что пуля в салоне не изменила траекторию, определите её скорость.
Дано:
\(u=72\ \text{км/ч}=20\ \text{м/с}\)
\(d=4\ \text{cм}=0,04\ \text{м}\)
\(a=1,5\ \text{м}\)
_______________
\(v-?\)
Построим чертеж движения, вид сверху. Направим ось ОХ по движению автомобиля относительно земли, ось ОУ – по движению пули относительно земли.
Если перейти в систему отсчета, связанную с автомобилем, земля «побежит» в обратном направлении со скоростью \(–u\), и траектория пули в салоне сместится (пунктирная линия на чертеже). Смещение на расстояние \(d\) за счет движения автомобиля происходит за время, в течение которого пуля пролетает от одной стенки салона к другой: $$ d=ut,\ \ t=\frac av $$ Откуда: $$ v=\frac ad u $$ Подставляем: $$ v=\frac{1,5}{0,04}\cdot 20=750\ (\text{м/с}) $$ Ответ: 750 м/с


