22.03.2021 14:56:06
Геометрия 10-11 класс

10 баллов
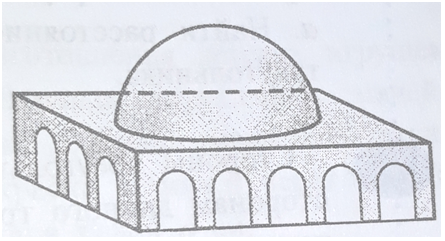
1. Купол концертного зала имеет форму полусферы. Площадь его поверхности - 900 м². Найти высоту купола. Ссылка на фото http://prnt.sc/10sfnhi
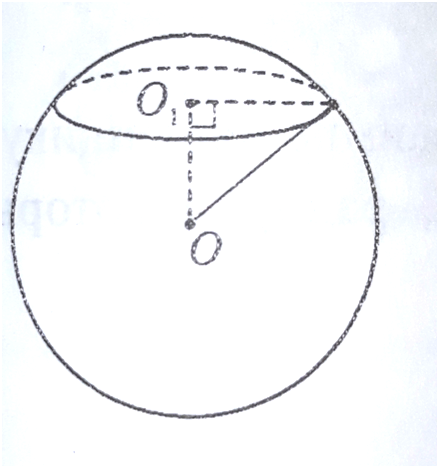
2. Шар пересекается удаленной от центра на расстоянии 20 см плоскостью. Радиус полученного круга - 20 см. Найти площадь поверхности шара (сферы). Ссылка на фото http://prnt.sc/10sfr1z
3. Площади двух сфер относятся, как 9:4. Найти отношение их радиусов.
2. Шар пересекается удаленной от центра на расстоянии 20 см плоскостью. Радиус полученного круга - 20 см. Найти площадь поверхности шара (сферы). Ссылка на фото http://prnt.sc/10sfr1z
3. Площади двух сфер относятся, как 9:4. Найти отношение их радиусов.

Ирина Каминкова
0
22.03.2021 17:07:38
1
Дано: полусфера, Sпов = 900 м²
Найти: h
Решение:
Высота купола равна радиусу полусферы.
Полная поверхность сферы S = 4πR² = 2*Sпов = 2*900 = 1800
R² = 1800/(4π) = 450/π
h = R = √(450/π) = 15√(2/π)
Ответ: 15√(2/π)
2
Дано: OO1 = 20 см, r = 20 см
Найти: Sпов
Решение:
По теореме Пифагора радиус шара
R = √(OO1² +r² ) = √(20²+20²) = 20√2 см
Площадь поверхности
Sпов = 4πR² = 4π(20√2)² = 3200π см²
Ответ: 3200π см²
3
Дано: две сферы, S1:S2 = 9:4
Найти: R1:R2
Решение:
Площадь поверхности пропорциональна квадрату радиуса. Поэтому
S1/S2 = (R1²)/(R2²) = (R1/R2)²
R1/R2 = √(S1/S2) = √(9/4) = 3/2
R1:R2 = 3:2
Ответ: 3:2
Дано: полусфера, Sпов = 900 м²
Найти: h
Решение:
Высота купола равна радиусу полусферы.
Полная поверхность сферы S = 4πR² = 2*Sпов = 2*900 = 1800
R² = 1800/(4π) = 450/π
h = R = √(450/π) = 15√(2/π)
Ответ: 15√(2/π)
2
Дано: OO1 = 20 см, r = 20 см
Найти: Sпов
Решение:
По теореме Пифагора радиус шара
R = √(OO1² +r² ) = √(20²+20²) = 20√2 см
Площадь поверхности
Sпов = 4πR² = 4π(20√2)² = 3200π см²
Ответ: 3200π см²
3
Дано: две сферы, S1:S2 = 9:4
Найти: R1:R2
Решение:
Площадь поверхности пропорциональна квадрату радиуса. Поэтому
S1/S2 = (R1²)/(R2²) = (R1/R2)²
R1/R2 = √(S1/S2) = √(9/4) = 3/2
R1:R2 = 3:2
Ответ: 3:2