22.03.2021 14:31:31
Геометрия 10-11 класс

10 баллов
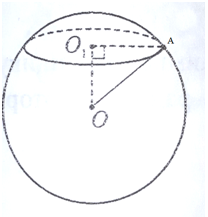
1. Плоскость, проведенная через конечную точку радиуса шара, образует с этим радиусом угол в 30°, радиус равен 4 см. Найти площадь сечения.
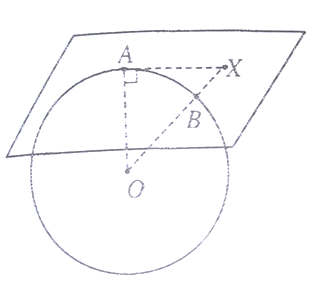
2. Точка X принадлежит касательной к шару плоскости и удалена от точки касания A на расстоянии 8 см. Центр шара - точка O, луч OX пересекает шар в точке B. Радиус шара 6 см. Найти длину отрезка XB.
Ссылка на фото http://prnt.sc/10ses9a
3. Если радиус сферы - R, тогда её площадь равна
2. Точка X принадлежит касательной к шару плоскости и удалена от точки касания A на расстоянии 8 см. Центр шара - точка O, луч OX пересекает шар в точке B. Радиус шара 6 см. Найти длину отрезка XB.
Ссылка на фото http://prnt.sc/10ses9a
3. Если радиус сферы - R, тогда её площадь равна

Ирина Каминкова
0
22.03.2021 17:16:45
1
Дано: сфера, OA = R = 4 см, ∠OAO1 = 30°
Найти: Sсеч
Решение:
Радиус сечения r = OA*cos 30° = 4*√3/2 = 2√3 см
Площадь сечения
Sсеч = πr² = π(2√3)² = 12π см²
Ответ: 12π см²
2
Дано: сфера, OA=OB=R=6 см, AX=8 см
Найти: XB
Решение:
По теореме Пифагора OX = √(OA²+AX²) = √(6²+8²) = 10 см
XB=OX-OB = 10-6 = 4 см
Ответ: 4 см
3
Площадь поверхности сферы равна S = 4πR²
Дано: сфера, OA = R = 4 см, ∠OAO1 = 30°
Найти: Sсеч
Решение:
Радиус сечения r = OA*cos 30° = 4*√3/2 = 2√3 см
Площадь сечения
Sсеч = πr² = π(2√3)² = 12π см²
Ответ: 12π см²
2
Дано: сфера, OA=OB=R=6 см, AX=8 см
Найти: XB
Решение:
По теореме Пифагора OX = √(OA²+AX²) = √(6²+8²) = 10 см
XB=OX-OB = 10-6 = 4 см
Ответ: 4 см
3
Площадь поверхности сферы равна S = 4πR²