16.03.2021 11:17:08
Геометрия 10-11 класс

10 баллов
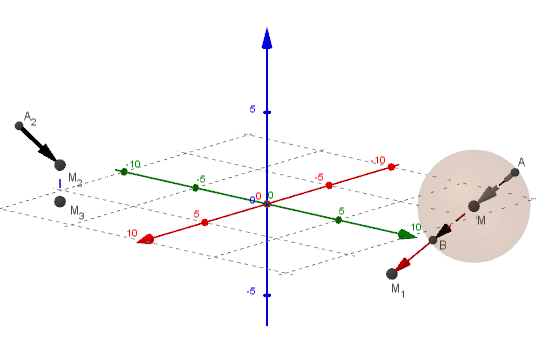
Точки A(−5;13;3) и B(−3;9;−1) симметричны относительно относительно точки M. Найдите:
а) координаты точки M1 при параллельном переносе точки M на вектор АВ
б) координаты вектораА2М2 симметричного вектору АМотносительно оси Oz
в) координаты точки M3 симметричной точке M2 относительно плоскости Oxy
г) скалярное произведение векторов АМ и а(4;8;-1)
д) уравнение сферы с диаметром AB
а) координаты точки M1 при параллельном переносе точки M на вектор АВ
б) координаты вектораА2М2 симметричного вектору АМотносительно оси Oz
в) координаты точки M3 симметричной точке M2 относительно плоскости Oxy
г) скалярное произведение векторов АМ и а(4;8;-1)
д) уравнение сферы с диаметром AB

Ирина Каминкова
0
16.03.2021 14:34:09
Точка M - середина отрезка AB
Μ = ((-5-3)/2; (13+9)/2;(3-1)/2) = (-4;11;1)
а) →AB = (-3+5;9-13;-1-3) = (2;-4;-4)
M₁ = M + →AB = (-4+2;-4+11; 1-4) = (-2;7;-3)
б) При симметрии относительно оси Oz
x→-x; y→-y; z→z
A₂ = (5;-13;3)
M₂ = (4;-11;1)
→AM = (1;-2;-2)
→A₂M₂ = (-1;2;-2)
в) При симметрии относительно оси Oxy
x→x; y→y; z→ -z
M₃ = (4;-11;-1)
г) →AM ∙ →a = 1*4-2*8-2*(-1) = 4-16+2 = -10
д) Центр сферы M(-4;11;1), радиус сферы R = AM
AM = √(1²+2²+2²) = 3
Уравнение сферы
(x+4)²+(y-11)²+(z-1)² = 9
Μ = ((-5-3)/2; (13+9)/2;(3-1)/2) = (-4;11;1)
а) →AB = (-3+5;9-13;-1-3) = (2;-4;-4)
M₁ = M + →AB = (-4+2;-4+11; 1-4) = (-2;7;-3)
б) При симметрии относительно оси Oz
x→-x; y→-y; z→z
A₂ = (5;-13;3)
M₂ = (4;-11;1)
→AM = (1;-2;-2)
→A₂M₂ = (-1;2;-2)
в) При симметрии относительно оси Oxy
x→x; y→y; z→ -z
M₃ = (4;-11;-1)
г) →AM ∙ →a = 1*4-2*8-2*(-1) = 4-16+2 = -10
д) Центр сферы M(-4;11;1), радиус сферы R = AM
AM = √(1²+2²+2²) = 3
Уравнение сферы
(x+4)²+(y-11)²+(z-1)² = 9