05.03.2021 19:16:48
Геометрия 10-11 класс

10 баллов
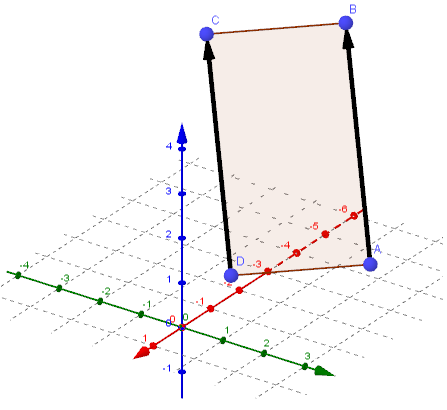
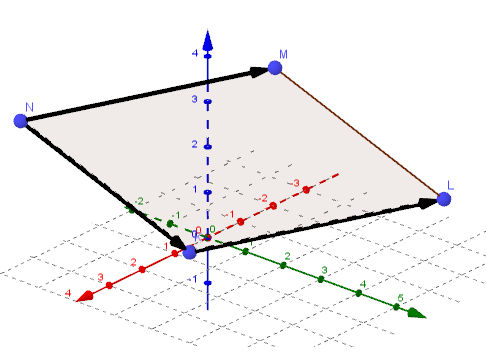
428)Является ли точки: а)А(2;6;4),В(0;4;8),С(2;2;8),D(4;4;4) вершинами параллелограмма АВСD; б) М(6;7;8),N(8;2;6),К(4;3;2),L(2;8;4) вершинами ромба МNКL?
431) Докажите, что треугольник с вершинами А(7;1;-5), В(4;-3;-4),С(1;3;-2) – равнобедренный, и найдите длину его меньшей медианы.
431) Докажите, что треугольник с вершинами А(7;1;-5), В(4;-3;-4),С(1;3;-2) – равнобедренный, и найдите длину его меньшей медианы.

Ирина Каминкова
0
05.03.2021 19:55:07
428
a)
→AB = (0-2;4-6;8-4) = (-2;-2;4)
→DC = (2-4;2-4;8-4) = (-2;-2;4)
→AB = →DC ⟹ AB || DC и AB=DC ⟹ABCD - параллелограмм
б)
→KL = (2-4;8-3;4-2) = (-2;5;2)
→NM = (6-8;7-2;8-6) = (-2;5;2)
→KL = →NM ⟹ KL||NM и KL=NM ⟹ MNKL - параллелограмм
→ NK = (4-8;3-2;2-6) = (-4;1;-4)
|KL| = √(2²+5²+2²) = √33
|NK| = √(4²+1²+4²) = √33
KL = NK ⟹ параллелограмм MNKL - ромб
------------------------------------------------------------------------------
431
→BC = (1-4;3+3;-2+4) = (-3;6;2)
→AC = (1-7;3-1;-2+5) = (-6;2;3)
→AB = (4-7;-3-1;-4+5) = (-3;-4;1)
|BC| = √(3²+6²+2²) = 7
|AC| = √(6²+2²+3²) = 7
AC=BC ⟹ ΔABC - равнобедренный с основанием AB
|AB| = √(3²+4²+1²) = √26 меньше AC ⟹ угол С при вершине наименьший
Значит, меньшая медиана - из вершины основания к боковой стороне
M - середина AC
M((7+1)/2; (1+3)/2;(-5-2)/2)
M(4;2;-3,5)
→BM = (4-4;2+3;-3,5+4) = (0;5;0,5)
|BM| = √(5² + 0,5²) = √(25 + 1/4) = √101/ 2
a)
→AB = (0-2;4-6;8-4) = (-2;-2;4)
→DC = (2-4;2-4;8-4) = (-2;-2;4)
→AB = →DC ⟹ AB || DC и AB=DC ⟹ABCD - параллелограмм
б)
→KL = (2-4;8-3;4-2) = (-2;5;2)
→NM = (6-8;7-2;8-6) = (-2;5;2)
→KL = →NM ⟹ KL||NM и KL=NM ⟹ MNKL - параллелограмм
→ NK = (4-8;3-2;2-6) = (-4;1;-4)
|KL| = √(2²+5²+2²) = √33
|NK| = √(4²+1²+4²) = √33
KL = NK ⟹ параллелограмм MNKL - ромб
------------------------------------------------------------------------------
431
→BC = (1-4;3+3;-2+4) = (-3;6;2)
→AC = (1-7;3-1;-2+5) = (-6;2;3)
→AB = (4-7;-3-1;-4+5) = (-3;-4;1)
|BC| = √(3²+6²+2²) = 7
|AC| = √(6²+2²+3²) = 7
AC=BC ⟹ ΔABC - равнобедренный с основанием AB
|AB| = √(3²+4²+1²) = √26 меньше AC ⟹ угол С при вершине наименьший
Значит, меньшая медиана - из вершины основания к боковой стороне
M - середина AC
M((7+1)/2; (1+3)/2;(-5-2)/2)
M(4;2;-3,5)
→BM = (4-4;2+3;-3,5+4) = (0;5;0,5)
|BM| = √(5² + 0,5²) = √(25 + 1/4) = √101/ 2