02.03.2021 17:06:12
Геометрия 10-11 класс

10 баллов
Длина ребра куба ABCDA1B1C1D1 равна 6 см .Вычислите расстояние между прямой AB и плоскостью B1CD

Ирина Каминкова
0
02.03.2021 17:27:05
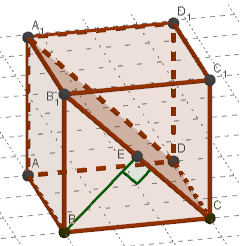
Дано: ABCDA1B1C1D1 - куб, а = 6 см - длина ребра
Найти: d(AB; B1CD)
Решение:
AB || A1B1 и A1B1⊂ B1CD. Значит, AB || B1CD
Искомое расстояние - перпендикуляр из B на B1CD
BE⊥B1CD и BE⊂ B1CB ⟹ BE⊥ B1C и d(AB; B1CD) = BE
Δ CBB1 - равнобедренный с BC=BB1, BE - высота и медиана
Площадь Δ CBB1
S = BC*BB1/2 = CB1*BE/2
BE = BC*BB1/CB1 = a*a/(a√2) = a/√2 = a√2 /2
BE = 6*√2 /2=3√2 см
Ответ: 3√2 см
Найти: d(AB; B1CD)
Решение:
AB || A1B1 и A1B1⊂ B1CD. Значит, AB || B1CD
Искомое расстояние - перпендикуляр из B на B1CD
BE⊥B1CD и BE⊂ B1CB ⟹ BE⊥ B1C и d(AB; B1CD) = BE
Δ CBB1 - равнобедренный с BC=BB1, BE - высота и медиана
Площадь Δ CBB1
S = BC*BB1/2 = CB1*BE/2
BE = BC*BB1/CB1 = a*a/(a√2) = a/√2 = a√2 /2
BE = 6*√2 /2=3√2 см
Ответ: 3√2 см