25.02.2021 22:09:09
Геометрия 7-9 класс
10 баллов
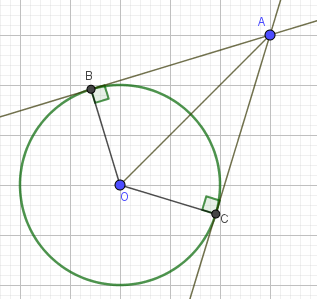
Из точки А к окружности с центром О проведены касательные АВ и АС. Длина ОВ=2. Отрезок, соединяющий точку А с центром окружности равен 4. Найти угол ВОС
Ирина Каминкова
0
25.02.2021 22:34:23
Дано: окружность, центр О, AB, AC - касательные, B,C - точки касания
ОВ=2, ОА = 4
Найти: ∠BOC
Решение:
В точке касания касательная перпендикулярна радиусу AB⊥OB, AC⊥OC
OB = OC = R, OA - общая сторона → (по гипотенузе и катету) ΔAOB = ΔAOC →
→ ∠AOB = ∠AOC → ∠BOC = 2∠AOB
cos∠AOB = OB/OA = 2/4 = 1/2
∠AOB = 60°
∠BOC = 2*60° = 120°
ОВ=2, ОА = 4
Найти: ∠BOC
Решение:
В точке касания касательная перпендикулярна радиусу AB⊥OB, AC⊥OC
OB = OC = R, OA - общая сторона → (по гипотенузе и катету) ΔAOB = ΔAOC →
→ ∠AOB = ∠AOC → ∠BOC = 2∠AOB
cos∠AOB = OB/OA = 2/4 = 1/2
∠AOB = 60°
∠BOC = 2*60° = 120°
Ответ эксперта
