17.02.2021 17:13:28
Геометрия 10-11 класс

10 баллов
Какое из утверждений является правильным?
- Из одной точки можно провести только одну наклонную к плоскости
- Если наклонные проведены из одной точки, то большей наклонной соответствует большая проекция
- Две прямые, перпендикулярные к одной плоскости, является перпендикулярными между собой
- Из точки на плоскость опущен перпендикуляр и наклонная. Перпендикуляр может быть больше наклонной
2. Наклонная, проведенная к плоскости, равна 6 см. Найдите проекцию этой наклонной на плоскость, если наклонная образует с плоскостью проекции угол 60 °.
3. В треугольнике ABC дано: AC = 6 см, BC = 8 см, ∠C = 90 °, CM - медиана. Через вершину C проведена прямая CD, перпендикулярная к плоскости треугольника ABC, причем CD = 12 см. Найти DM.
------------------------------------------------------------------------------------------------------------
Яке з тверджень є правильним?
- З однієї точки можна провести лише одну похилу до площини
- Якщо похилі проведені з однієї точки, то більшій похилій відповідає більша проекція
- Дві прямі, перпендикулярні до однієї площини, є перпендикулярними між собою
- З точки на площину опущений перпендикуляр і похила. Перпендикуляр може бути більшим за похилу
2.Похила, проведена до площини, дорівнює 6 см. Знайдіть проекцію цієї похилої на площину, якщо похила утворює з площиною проекції кут 60°.
3.У трикутнику ABC дано: AC=6 см, BC=8 см, ∠C=90°, CM – медіана. Через вершину C проведено пряму CD, перпендикулярну до площини трикутника ABC, причому CD=12 см. Знайти DM.
- Из одной точки можно провести только одну наклонную к плоскости
- Если наклонные проведены из одной точки, то большей наклонной соответствует большая проекция
- Две прямые, перпендикулярные к одной плоскости, является перпендикулярными между собой
- Из точки на плоскость опущен перпендикуляр и наклонная. Перпендикуляр может быть больше наклонной
2. Наклонная, проведенная к плоскости, равна 6 см. Найдите проекцию этой наклонной на плоскость, если наклонная образует с плоскостью проекции угол 60 °.
3. В треугольнике ABC дано: AC = 6 см, BC = 8 см, ∠C = 90 °, CM - медиана. Через вершину C проведена прямая CD, перпендикулярная к плоскости треугольника ABC, причем CD = 12 см. Найти DM.
------------------------------------------------------------------------------------------------------------
Яке з тверджень є правильним?
- З однієї точки можна провести лише одну похилу до площини
- Якщо похилі проведені з однієї точки, то більшій похилій відповідає більша проекція
- Дві прямі, перпендикулярні до однієї площини, є перпендикулярними між собою
- З точки на площину опущений перпендикуляр і похила. Перпендикуляр може бути більшим за похилу
2.Похила, проведена до площини, дорівнює 6 см. Знайдіть проекцію цієї похилої на площину, якщо похила утворює з площиною проекції кут 60°.
3.У трикутнику ABC дано: AC=6 см, BC=8 см, ∠C=90°, CM – медіана. Через вершину C проведено пряму CD, перпендикулярну до площини трикутника ABC, причому CD=12 см. Знайти DM.

Ирина Каминкова
0
17.02.2021 18:14:01
1
Если наклонные проведены из одной точки, то большей наклонной соответствует большая проекция
Если наклонные проведены из одной точки, то большей наклонной соответствует большая проекция

Ирина Каминкова
0
17.02.2021 18:16:12
2
Дано: AB - наклонная, A1B - проекция
∠ABA1 = 60°, AB = 6 см
Найти: A1B
Решение:
ΔA1BA - прямоугольный, ∠A1 = 90°
A1B = AB * cos 60°= 6*1/2 = 3 см
Дано: AB - наклонная, A1B - проекция
∠ABA1 = 60°, AB = 6 см
Найти: A1B
Решение:
ΔA1BA - прямоугольный, ∠A1 = 90°
A1B = AB * cos 60°= 6*1/2 = 3 см

Ирина Каминкова
0
17.02.2021 18:23:49
3
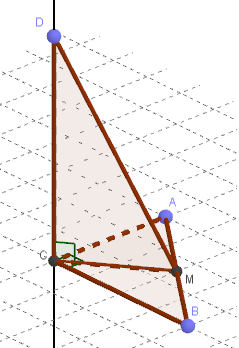
Дано: ΔABC, AC = 6 см, BC = 8 см, ∠C = 90 °, CM - медиана
CD⊥ABC, CD = 12 см
Найти: DM
Решение:
Точка M является центром окружности, которую можно описать вокруг ΔABC
MC=MA=MB = AB/2
AB=√(AC² + BC²) = √(6²+8²) = 10 см
MC = 10/2 = 5 см
ΔDCM - прямоугольный, по т-ме Пифагора
DM=√(CD² + MC²) = √(12² + 5²) = 13 см
Дано: ΔABC, AC = 6 см, BC = 8 см, ∠C = 90 °, CM - медиана
CD⊥ABC, CD = 12 см
Найти: DM
Решение:
Точка M является центром окружности, которую можно описать вокруг ΔABC
MC=MA=MB = AB/2
AB=√(AC² + BC²) = √(6²+8²) = 10 см
MC = 10/2 = 5 см
ΔDCM - прямоугольный, по т-ме Пифагора
DM=√(CD² + MC²) = √(12² + 5²) = 13 см