24.01.2021 11:51:59
Геометрия 10-11 класс

10 баллов
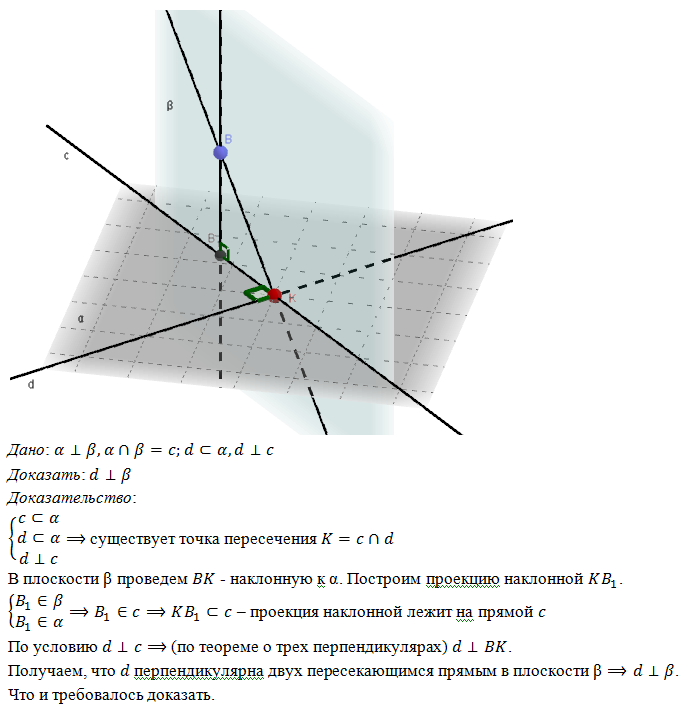
Плоскости а и β взаимно перпендикулярны и пересекаются по прямой с. Докажите, что любая прямая плоскости а, перпендикулярная к прямой с, перпендикулярна к плоскости β.

Азамат Байбалинов
0
24.01.2021 12:29:32
Проведем в плоскости α произвольную прямую АС, перпендикулярную к прямой с, C∈c. Докажем, что CA⊥β.
В плоскости β через точку С проведем прямую СВ, перпендикулярную к прямой с. Так как СА⊥c и CB⊥c, то ∠АСВ — линейный угол одного из двугранных углов, образованных плоскостями α и β. По условию задачи α ⊥ β, поэтому ∠АСВ — прямой, т.е. CA⊥CB. Таким образом, прямая СА перпендикулярна к двум пересекающимся прямым с и СВ плоскости β, поэтому CA⊥β.
В плоскости β через точку С проведем прямую СВ, перпендикулярную к прямой с. Так как СА⊥c и CB⊥c, то ∠АСВ — линейный угол одного из двугранных углов, образованных плоскостями α и β. По условию задачи α ⊥ β, поэтому ∠АСВ — прямой, т.е. CA⊥CB. Таким образом, прямая СА перпендикулярна к двум пересекающимся прямым с и СВ плоскости β, поэтому CA⊥β.