22.04.2021 22:53:06
Геометрия 10-11 класс

10 баллов
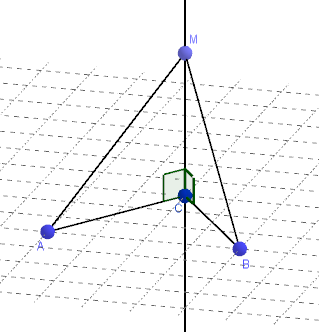
1) Точки A, В, С принадлежат плоскости альфа, прямая МС перпендикулярна к ней. Докажите равенство отрезков АС і ВС, если известно, что точка М равноудалена от точек А и В
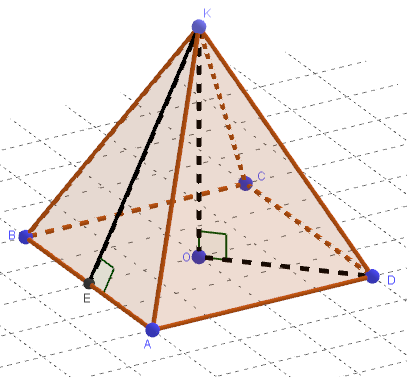
2) Точка К не принадлежит плоскости квадрата АВСD, KO- перпендикуляр к плоскости квадрата, точка O - центр вписанной окружности. Найдите расстояние от точки К до середины стороны АВ, если DО = 8 см, КО = 7 см
2) Точка К не принадлежит плоскости квадрата АВСD, KO- перпендикуляр к плоскости квадрата, точка O - центр вписанной окружности. Найдите расстояние от точки К до середины стороны АВ, если DО = 8 см, КО = 7 см

Ирина Каминкова
0
23.04.2021 10:26:27
1
Дано: {A,B,C} є α, MC⊥α, MA=MB
Доказать: AC=BC
Доказательство:
Рассмотрим ΔAMC и ΔBMC
∠ACM=∠BCM = 90°
MC - общий катет
AC=BC
По двум сторонам и углу между ними ΔAMC = ΔBMC ⟹ AC=BC
Что и требовалось доказать.
--------------------------------------------------------------------------------
2
Дано: ABCD - квадрат, О - центр вписанной окружности, KO⊥(ABC)
DО = 8 см, КО = 7 см, E - середина AB
Найти: KE
Решение:
В квадрате центр вписанной окружности совпадает с центром описанной окружности.
Значит, пирамида KABCD - правильная, все ребра равны, все апофемы равны.
Найдем апофему KE
Из ΔDOK по теореме Пифагора ребро KD =√(KO²+DO²) = √(7²+8²) = √113 см
KD=KA=KB=KC
Диагональ квадрата BD =2DO = 16 см
Сторона квадрата AB = BD/√2 = 16/√2 = 8√2 см
Половина стороны квадрата AE = AB/2 = 4√2 см
Из ΔAKE по теореме Пифагора апофема KE = √(AK²-AE²) = √(113-32) = √81 = 9 см
Ответ: 9 см
Дано: {A,B,C} є α, MC⊥α, MA=MB
Доказать: AC=BC
Доказательство:
Рассмотрим ΔAMC и ΔBMC
∠ACM=∠BCM = 90°
MC - общий катет
AC=BC
По двум сторонам и углу между ними ΔAMC = ΔBMC ⟹ AC=BC
Что и требовалось доказать.
--------------------------------------------------------------------------------
2
Дано: ABCD - квадрат, О - центр вписанной окружности, KO⊥(ABC)
DО = 8 см, КО = 7 см, E - середина AB
Найти: KE
Решение:
В квадрате центр вписанной окружности совпадает с центром описанной окружности.
Значит, пирамида KABCD - правильная, все ребра равны, все апофемы равны.
Найдем апофему KE
Из ΔDOK по теореме Пифагора ребро KD =√(KO²+DO²) = √(7²+8²) = √113 см
KD=KA=KB=KC
Диагональ квадрата BD =2DO = 16 см
Сторона квадрата AB = BD/√2 = 16/√2 = 8√2 см
Половина стороны квадрата AE = AB/2 = 4√2 см
Из ΔAKE по теореме Пифагора апофема KE = √(AK²-AE²) = √(113-32) = √81 = 9 см
Ответ: 9 см