31.03.2021 10:23:08
Геометрия 10-11 класс

10 баллов
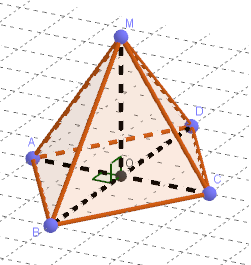
ABCD-ромб со стороной 5 см. Через точку О пересечения диагоналей проведена прямая OM, перпендикулярная плоскости ромба . Найдите расстояние от M до вершин ромба, если MO=8 см, AC= 6см

Ирина Каминкова
0
31.03.2021 11:52:07
Дано: ABCD - ромб, AB = 5 см, AC = 6 см
O = AC ∩ BD, MO⊥(ABC), MO = 8 см
Найти: AM, BM, CM, DM
Решение:
Диагонали ромба перпендикулярны и делятся точкой пересечения пополам.
AO=AC/2 = 3 см
Из ΔΑΟΒ по теореме Пифагора BO = √AB² - AO²) = √(5²-3²) = 4 см
Из ΔΑΟM по теореме Пифагора AM = √AO² + MO²) = √(3²+8²) = √73 см
Из ΔBΟM по теореме Пифагора BM = √BO² + MO²) = √(4²+8²) = 4√(1²+2²) = 4√5 см
ΔCΟM = ΔΑΟM по двум сторонам и углу между ними ⟹ CM = AM = √73 см
ΔDΟM = ΔBΟM по двум сторонам и углу между ними ⟹ DM = BM = 4√5 см
Ответ: AM = CM = √73 см
BM = DM = 4√5 см
O = AC ∩ BD, MO⊥(ABC), MO = 8 см
Найти: AM, BM, CM, DM
Решение:
Диагонали ромба перпендикулярны и делятся точкой пересечения пополам.
AO=AC/2 = 3 см
Из ΔΑΟΒ по теореме Пифагора BO = √AB² - AO²) = √(5²-3²) = 4 см
Из ΔΑΟM по теореме Пифагора AM = √AO² + MO²) = √(3²+8²) = √73 см
Из ΔBΟM по теореме Пифагора BM = √BO² + MO²) = √(4²+8²) = 4√(1²+2²) = 4√5 см
ΔCΟM = ΔΑΟM по двум сторонам и углу между ними ⟹ CM = AM = √73 см
ΔDΟM = ΔBΟM по двум сторонам и углу между ними ⟹ DM = BM = 4√5 см
Ответ: AM = CM = √73 см
BM = DM = 4√5 см