19.03.2021 09:26:30
Алгебра 10-11 класс

10 баллов
3.Найти первообразную f(x)=x^2+3sin x ; f(x)=1/cos^2x-cos(3x-1)
4. Найти такую первообразную, график которой проходит чрез точку М:
f(x)=x^3+1-3/cos^2x; M(0;-2)
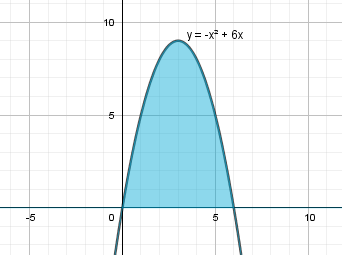
5.Вычислить площадь фигуры, ограниченной линиями: y=6x-x^2 ; y=0
4. Найти такую первообразную, график которой проходит чрез точку М:
f(x)=x^3+1-3/cos^2x; M(0;-2)
5.Вычислить площадь фигуры, ограниченной линиями: y=6x-x^2 ; y=0

Ирина Каминкова
1
19.03.2021 15:18:08
3
f(x)=x^2+3sin x
F(x) = x³/3 + 3cos x + C
f(x)=1/cos^2 x-cos(3x-1)
F(x) = tg x +(1/3) * sin(3x-1) + C
4
f(x)=x^3+1-3/cos^2x
F(x) = x⁴/4 - 3 tg x + C
F(0) = 0 - 0 + C = -2, C = -2
Искомая первообразная F(x) = x⁴/4 - 3 tg x -2
5
y=6x-x^2 = x(6-x)
Парабола ветками вниз, точки пересечения с осью оХ x1 = 0, x2 = 6
Площадь
S = ∫ [0;6] (6x-x^2) dx = (6x²/2-x³/3) |[0;6] = (3x²-x³/3) |[0;6] = 3*6² - 6³/3 =
= 108 - 72 = 36
f(x)=x^2+3sin x
F(x) = x³/3 + 3cos x + C
f(x)=1/cos^2 x-cos(3x-1)
F(x) = tg x +(1/3) * sin(3x-1) + C
4
f(x)=x^3+1-3/cos^2x
F(x) = x⁴/4 - 3 tg x + C
F(0) = 0 - 0 + C = -2, C = -2
Искомая первообразная F(x) = x⁴/4 - 3 tg x -2
5
y=6x-x^2 = x(6-x)
Парабола ветками вниз, точки пересечения с осью оХ x1 = 0, x2 = 6
Площадь
S = ∫ [0;6] (6x-x^2) dx = (6x²/2-x³/3) |[0;6] = (3x²-x³/3) |[0;6] = 3*6² - 6³/3 =
= 108 - 72 = 36