11.03.2021 16:49:58
Геометрия 10-11 класс
10 баллов
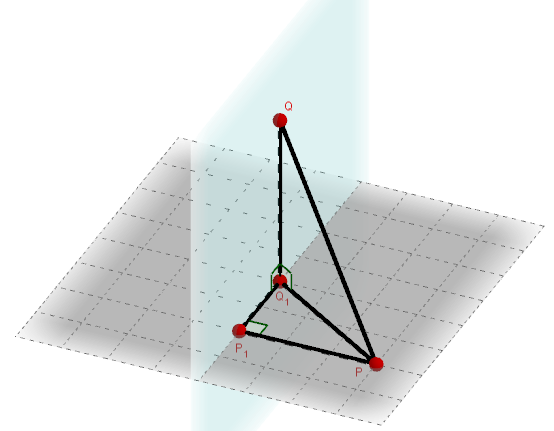
Из точки p и q лежащих в двух перпендикулярных плоскостях,проведены перпендикуляры PP1 и QQ1 на прямую пересечения плоскостей.Найдите длину отрезка PQ если P1Q1=2см,PP1=3см,QQ1=6см.
Ирина Каминкова
0
11.03.2021 17:12:11
Дано: α⊥β, α∩β = P1Q1
P є α, Q є β, PP1⊥P1Q1, QQ1⊥P1Q1
P1Q1=2см, PP1=3см, QQ1=6см
Найти: PQ
Решение:
PP1⊥P1Q1 ⟹ ΔPP1Q1 - прямоугольный с ∠P1 = 90°
По теореме Пифагора PQ1 = √(P1Q1²+PP1²) = √(2²+3²) = √13 см
α⊥β и QQ1⊥P1Q1⟹ ΔQQ1P - прямоугольный с ∠Q1 = 90°
По теореме Пифагора PQ = √(QQ1²+PQ1²) = √(6²+13) = √49 = 7 см
Ответ: 7 см
P є α, Q є β, PP1⊥P1Q1, QQ1⊥P1Q1
P1Q1=2см, PP1=3см, QQ1=6см
Найти: PQ
Решение:
PP1⊥P1Q1 ⟹ ΔPP1Q1 - прямоугольный с ∠P1 = 90°
По теореме Пифагора PQ1 = √(P1Q1²+PP1²) = √(2²+3²) = √13 см
α⊥β и QQ1⊥P1Q1⟹ ΔQQ1P - прямоугольный с ∠Q1 = 90°
По теореме Пифагора PQ = √(QQ1²+PQ1²) = √(6²+13) = √49 = 7 см
Ответ: 7 см
Ответ эксперта
