25.02.2021 19:35:30
Геометрия 10-11 класс

10 баллов
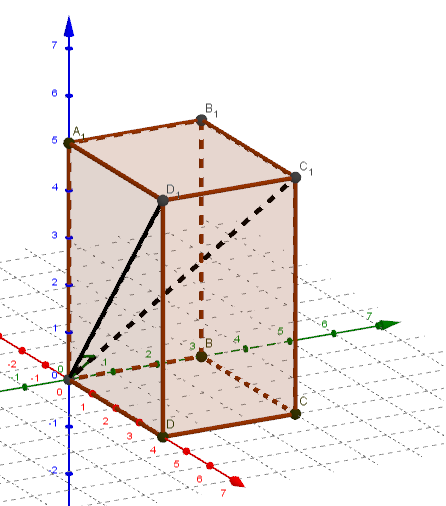
В прямоугольном параллелепипеде ABCDA1B1C1D1 найдите cинус угла между плоскостью ADD1 и прямой AC1, если AA1 = 5, AB = 3, BC = 4. Запишите ответ, умноженный на √50. Постарайтесь решить задачу с помощью векторов

Ирина Каминкова
0
25.02.2021 20:11:36
Проекцией т.С1 на плоскость ADD1 будет т.D1
Проекцией прямой АС1 на плоскость ADD1 будет прямая АD1
∠C1AD1 - искомый угол. Обозначим его ∠C1AD1 = α
Координаты точек A(0;0;0), C1(4;3;5), D1(4;0;5)
→АС1 = (4;3;5)
|AC1| = √(4²+3²+5²) = √50
→АD1 = (4;0;5)
|AD1| = √(4²+0²+5²) = √41
cos α = (→АС1 ∙ →АD1) / (|AC1|∙|AD1| ) = (4*4+3*0+5*5)/(√50∙√41) = √(41/50)
sin α = √(1-cos² α) = √(1-41/50) = √(9/50) = 3/√50
Ответ: 3
Проекцией прямой АС1 на плоскость ADD1 будет прямая АD1
∠C1AD1 - искомый угол. Обозначим его ∠C1AD1 = α
Координаты точек A(0;0;0), C1(4;3;5), D1(4;0;5)
→АС1 = (4;3;5)
|AC1| = √(4²+3²+5²) = √50
→АD1 = (4;0;5)
|AD1| = √(4²+0²+5²) = √41
cos α = (→АС1 ∙ →АD1) / (|AC1|∙|AD1| ) = (4*4+3*0+5*5)/(√50∙√41) = √(41/50)
sin α = √(1-cos² α) = √(1-41/50) = √(9/50) = 3/√50
Ответ: 3