Законы Ньютона
п.1. Первый закон Ньютона
Ньютон обобщил закон инерции Галилея (см. §17 данного справочника) в следующей формулировке.
Существуют такие системы отсчета, называемые инерциальными, в которых материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока на неё не действуют никакие силы (или пока равнодействующая всех сил равна 0).
Доказать первый закон Ньютона с помощью прямого эксперимента невозможно, т.к. ни в коем случае не удастся полностью исключить влияние окружающих тел.
Тем не менее, для большого класса задач этим влиянием можно пренебречь или учесть его позже, в виде поправок к основной физической модели.
Например, систему отсчета, связанную с Землей, можно считать инерциальной, если в задаче можно пренебречь: 1) изменением скорости движения Земли как планеты (при вращении вокруг своей оси, вокруг Солнца, при взаимодействии с Луной);
2) кривизной поверхности Земли, по которой движутся рассматриваемые тела;
3) размерами движущихся тел, считая их материальными точками (см. §5 данного справочника).
Если известна хотя бы одна инерциальная система отсчета, то инерциальными будут любые другие системы отсчета, которые движутся относительно неё равномерно и прямолинейно.
Так, если мы принимаем систему отсчета, связанную с Землей, в качестве инерциальной, то система отсчета, связанная с поездом или автомобилем, который движется по Земле прямолинейно и равномерно, также будет инерциальной.
Все механические явления протекают одинаково во всех инерциальных системах отсчета.
Принцип относительности даёт обоснование для выбора «наиболее удобной» инерциальной системы отсчета при описании того или иного явления. Удобство в данном случае заключается в простоте и наглядности получаемых уравнений движения.
п.2. Второй закон Ньютона
Ускорение тела прямо пропорционально силе, действующей на него, и обратно пропорционально массе тела: $$ \overrightarrow{a}=\frac{\overrightarrow{F}}{m} $$ При действии на тело нескольких сил ускорение определяется равнодействующей всех сил: $$ \overrightarrow{a}=\frac{\overrightarrow{F_1}+\overrightarrow{F_2}+...}{m} $$
В этом законе выражается принцип причинности: сила является причиной ускорения данного тела.
п.3. Третий закон Ньютона
Силы, с которыми взаимодействующие тела действуют друг на друга, направлены вдоль одной прямой, равны по модулю и противоположны по направлению: $$ \overrightarrow{F_1}=-\overrightarrow{F_2} $$
Упрощенно третий закон Ньютона можно сформулировать так: «сила действия равна силе противодействия».
Применяя третий закон Ньютона важно помнить, что:
- силы, возникающие при взаимодействии, приложены к разным телам; поэтому они НЕ уравновешивают друг друга и их бессмысленно складывать. Уравновешиваться могут только силы, приложенные к одному телу;
- силы, возникающие при взаимодействии, одной природы.
п.4. Границы применимости механики Ньютона
Законы классической механики, сформулированные Ньютоном, описывают движения материальных точек относительно инерциальных систем отсчета.
Они становятся неточными, если тела и системы начинают двигаться очень быстро, со скоростями порядка скорости света \(v\cong c=3\cdot 10^8\ \text{м/с}\) (такое движение называют релятивистским).
Также начинают действовать другие законы, если тела и системы становятся слишком малыми, порядка размеров атомов \(r\cong 10^{-9}\ \text{м}\) (в этом случае процессы становятся квантовыми).
Таким образом, границы применимости классической механики $$ v \lt\lt 3\cdot 10^8\frac{\text{м}}{\text{с}},\ \ r\gt\gt 10^{-9}\ \text{м} $$
п.5. Задачи
Задача 1. Считаем систему отсчета, связанную с Землей, инерциальной. Приведите примеры тел, движущихся относительно Земли, с которыми можно и нельзя связать инерциальную систему отсчета. Объясните, почему.
Велосипедист движется равномерно по прямой дороге
Да
Движение прямолинейное и равномерное
Велосипедист движется равномерно по круговой дорожке велотрека
Нет
Движение непрямолинейное
Поезд движется прямолинейно с ускорением
Нет
Движение неравномерное
Парашютист опускается прямолинейно и равномерно
Да
Движение прямолинейное и равномерное
Задача 2. При расчетах траектории космического корабля от Земли на Марс и обратно, можно ли считать инерциальной систему отсчета: а) связанную с Землей? б) связанную с Солнцем?
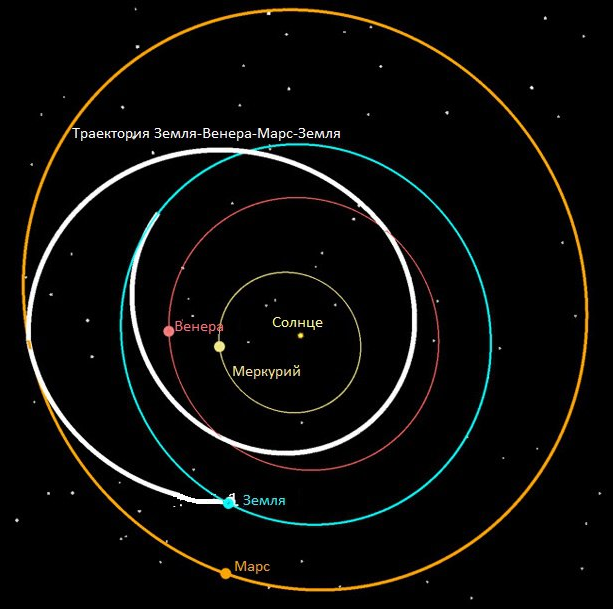 |
В данном случае пренебречь движением Земли вокруг Солнца нельзя. Т.к. это движение является неравномерным, с Землей нельзя связать ИСО. А вот система отсчета, связанная с Солнцем, с большой степенью точности будет инерциальной. Почему не идеально инерциальной? Потому что Солнце также участвует в сложных движениях с ускорением: 1) вокруг центра масс Солнечной системы; 2) вокруг центра Галактики; |
Ответ: а) нет; б) да.
Задача 3. Мальчик массой 40 кг толкнул мяч массой 800 г и придал ему ускорение 10 м/с2. С какой силой взаимодействуют мальчик и мяч? Какое ускорение получил мальчик при ударе?
Дано:
\(m_1=800\ \text{г}=0,8\ \text{кг}\)
\(a_1=10\ \text{м/с}^2\)
\(m_2=40\ \text{кг}\)
__________________
\(F-?,\ a_2-?\)
По третьему закону Ньютона сила действия мальчика на мяч равна силе действия мяча на мальчика: \(\overrightarrow{F_2}=-\overrightarrow{F_1}\). Модуль этих сил: \begin{gather*} F=m_1a_1=m_2a_2,\ \ a_2=\frac{F}{m_2}\\[6pt] F=0,8\cdot 10=8\ (\text{Н}),\ \ a_2=\frac{8}{40}=0,2\ (\text{м/с}^2) \end{gather*} Ответ: 0,8 Н; 0,2 м/с2


