Закон Архимеда

п.1. Выталкивание тела жидкостью при погружении

Проведем следующий опыт.

Нам понадобится: 1) динамометр; 2) груз; 3) стакан с раствором соли.

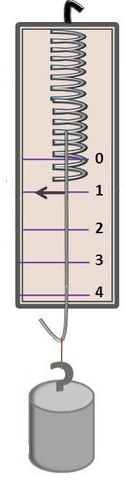Подвешиваем грузик на крючок динамометра, фиксируем показания динамометра.

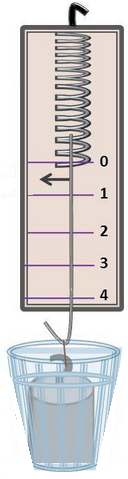Опускаем подвешенный грузик в стакан с раствором соли. Показания динамометра уменьшаются.

В первом случае пружина динамометра растягивается под действием силы тяжести: $$ F_\text{упр1}=F_\text{тяж}\Rightarrow kl_1=mg\Rightarrow l_1=\frac{mg}{k} $$

Во втором случае пружина растягивается под действием равнодействующей силы тяжести и некоторой силы, которая направлена вверх, т.е. выталкивает тело из жидкости: $$ F_\text{упр2}=R=F_\text{тяж}-F_\text{выт}\Rightarrow kl_2=mg-F_\text{выт}\Rightarrow l_2=\frac{mg-F_\text{выт}}{k} $$ Поэтому \(l_2\lt l_1\), во втором случае пружина растягивается меньше.

Вывод:

Действием выталкивающей силы можно объяснить, почему корабли не тонут в воде: если выталкивающая сила уравновешивает силу тяжести, то вода становится «опорой» и корабль держится на воде.

п.2. Выталкивание тела газом при погружении

Проведем следующий опыт.

Нам понадобится: 1) весы с разновесами; 2) колба с пробкой; 3) широкий сосуд; 4) источник углекислого газа.

Получить небольшое количество углекислого газа можно при взаимодействии разбавленной соляной кислоты и карбоната кальция (мрамора): $$ \mathrm{CaCO_3+2HCl\rightarrow CaCl_2+CO_2\uparrow +H_2O} $$

Реакцию следует проводить в пробирке с газоотводной трубкой. Она будет служить источником \(\mathrm{CO_2}\).

Закрываем колбу пробкой. Помещаем колбу в широкий сосуд, подвешиваем колбу к чашке весов и уравновешиваем её с помощью разновесов. Запускаем в сосуд газоотводную трубку с углекислым газом, плотность которого больше плотности воздуха. Углекислый газ скапливается и заполняет дно сосуда, равновесие весов нарушается. На колбу начинает действовать большая выталкивающая сила, чем выталкивающая сила в воздухе: $$ \rho_{\mathrm{CO_2}}\gt \rho_\text{возд}\Rightarrow F_{\text{выт. }\mathrm{CO_2}}\gt F_\text{выт. возд.} $$

Вывод:

п.3. Закон Архимеда

В истории науки первым, кто изучал выталкивающую силу, действующую на тела в воде, был древнегреческий ученый Архимед. Поэтому эту силу также называют силой Архимеда.

«Есть вещи, которые кажутся невероятными большинству людей, не изучавших математику». Архимед (287-212 гг. до н.э.), древнегреческий ученый и инженер

Рассмотрим тело, погружённое в жидкость. Сверху на тело действует сила \(F_1\), которая равна давлению столба жидкости высотой \(h_1\) на площадь верхней поверхности тела: \(F_1=\rho_\text{ж}gh_1S\). Снизу по закону Паскаля на тело действует сила \(F_2\), которая равна давлению столба жидкости высотой \(h_2\) на площадь нижней поверхности тела: \(F_2=\rho_\text{ж}gh_2S\).

На любом промежуточном уровне силы, действующие на боковые поверхности, равны по значению и противоположны по направлению, т.е. взаимно уравновешивают друг друга.

Равнодействующая всех сил, действующих на тело со стороны жидкости: $$ R=F_2-F-1=\rho_\text{ж}gS(h_2-h_1)=\rho_\text{ж}gSh=\rho_\text{ж}gV_\text{т} $$

Равнодействующая направлена вверх, т.е. является выталкивающей силой.

Архимедова сила зависит от:

• плотности среды (жидкости или газа);
• объема погруженного тела (объема погруженной части тела);
• силы притяжения (\(g\) зависит от массы планеты и расстояния до её центра; сила Архимеда будет разной на Земле и Луне; также, сила Архимеда будет заметно отличаться на поверхности Земли и на значительной высоте от Земли).

Архимедова сила НЕ зависит от:

• плотности вещества тела;
• части объема тела, не погруженной в среду.

п.4. Опыт с ведерком Архимеда

Для опыта понадобится: 1) ведерко Архимеда; 2) небольшой камень произвольной формы; 3) широкий сосуд с отливной трубкой; 4) стакан; 5) пружина; 6) штатив.

а) Укрепим пружину на штативе и подвесим к ней пустое ведерко (его называют ведерком Архимеда), а к ведерку – небольшой камень произвольной формы.

Отметим удлинение пружины.

Нальем в широкий сосуд с отливной трубкой воду до уровня отлива.

б) Подставим пустой стакан под отлив и погрузим камень полностью в воду. Камень вытеснит объем воды, равный собственному объему.

Удлинение пружины становится меньше - на камень действует выталкивающая сила.

в) Выльем воду из стакана в ведерко.

Удлинение пружины снова становится таким, как в начале.

Значит, выталкивающая сила равна весу воды в объеме погруженного в нее тела.

Таким образом, данный опыт подтверждает закон Архимеда.

п.5. Задачи

Задача 1. Чему равна сила Архимеда, действующая на полностью погруженный в воду куб с длиной ребра 8 см? Чему равна эта сила, если куб будет погружен в воду наполовину?

Дано:
\(a=8\ \text{см}=0,08\ \text{м}\)
\(\rho_{\text{ж}}=1000\ \text{кг/м}^3\)
\(g\approx 10\ \text{м/с}^2\)
__________________
\(F_A-?,\ F'_A-?\)

1) При полном погружении объем куба в воде \(V_{\text{Т}}=a^3.\)
Сила Архимеда \begin{gather*} F_A=\rho_{\text{ж}}V_{\text{Т}}g= \rho_{\text{ж}}a^3g \end{gather*} Подставляем \begin{gather*} F_A=1000\cdot 0,08^3\cdot 10=5,12\ {\text{Н}} \end{gather*} 2) Если куб погружен наполовину, его объем в воде \begin{gather*} V'_{\text{Т}}=\frac 12 a^3=\frac 12 V_{\text{Т}} \end{gather*} Сила Архимеда \begin{gather*} F'_A=\frac 12\rho_{\text{ж}}V_{\text{Т}}g= \frac 12 F_A \end{gather*} Сила уменьшается в 2 раза, т.к. объем погруженной части в 2 раза меньше. \begin{gather*} F'_A=\frac 12\cdot 5,12=2,56\ {\text{Н}} \end{gather*} Ответ: 1) 5,12 Н; 2) 2,56 Н

Задача 2. На полностью погруженный в воду медный шар массой 8,9 кг действует выталкивающая сила 20 Н. Сплошной ли шар или в нем есть полость? Чему равен объем полости, если она есть? Плотность меди 8900 кг/м³, g≈10 м/с². Ответ выразите в кубических дециметрах.

Дано:
\(m=8,9\ \text{кг}\)
\(\rho_{\text{ж}}=1000\ \text{кг/м}^3\)
\(F_A=20\ \text{Н}\)
\(g\approx 10\ \text{м/с}^2\)
\(\rho_{\text{м}}=8900\ \text{кг/м}^3\)
__________________
\(V_{\text{П}}-?\)

Сила Архимеда \begin{gather*} F_A=\rho_{\text{ж}}V_{\text{Т}}g\Rightarrow V_{\text{Т}}=\frac{F_A}{\rho_{\text{ж}}g} \end{gather*} Получаем $$ V_{\text{Т}}=\frac{20}{1000\cdot 10}=0,002\ (\text{м}^3) = \text{объем шара} $$ С другой стороны, \begin{gather*} V=\frac{m}{\rho_{\text{м}}} \end{gather*} Получаем $$ V=\frac{8,9}{8900}=0,001\ (\text{м}^3) = \text{объем вещества шара} $$ Т.к. \(V_{\text{Т}}\gt V\), в шаре есть полость.
Объем шара – это сумма объема вещества и объема полости: \(V_{\text{Т}}=V+V_{\text{П}}\)
\begin{gather*} V_{\text{П}}=V_{\text{Т}}-V\\[7pt] V_{\text{П}}=0,002-0,001=0,001\ (\text{м}^3)=1\ (\text{дм}^3) \end{gather*} Ответ: 1 дм³

Задача 3. Силы Архимеда, действующие на одно и то же тело в воде и в керосине, отличаются на 2 Н. В какой жидкости выталкивающая сила больше? Чему равен объем тела? Ответ выразите в кубических дециметрах.

Дано:
\(\Delta F_A=2\ \text{Н}\)
\(\rho_{\text{в}}=1000\ \text{кг/м}^3\)
\(\rho_{\text{к}}=800\ \text{кг/м}^3\)
\(g\approx 10\ \text{м/с}^2\)
__________________
\(V_{\text{Т}}-?\)

Сила Архимеда прямо пропорциональна плотности жидкости. Следовательно, она будет больше в воде. \begin{gather*} F_{A\text{в}}=\rho_{\text{в}}V_{\text{Т}}g,\\[7pt] F_{A\text{к}}=\rho_{\text{к}}V_{\text{Т}}g,\\[7pt] \Delta F_A=F_{A\text{в}}-F_{A\text{к}}=\rho_{\text{в}}V_{\text{Т}}g -\rho_{\text{к}}V_{\text{Т}}g=(\rho_{\text{в}}-\rho_{\text{к}})V_{\text{Т}}g \end{gather*} Объем тела \begin{gather*} V_{\text{Т}}=\frac{\Delta F_A}{(\rho_{\text{в}}-\rho_{\text{к}})}g \end{gather*} Получаем \begin{gather*} V_{\text{Т}}=\frac{2}{(1000-800)\cdot 10}=0,001\ (\text{м}^3)=1\ (\text{дм}^3) \end{gather*} Ответ: больше в воде; 1 дм³

Задача 4. Бетонная плита объёмом 2 м3 погружена в воду. Какую силу необходимо приложить, чтобы удержать её в воде; в воздухе?

Дано:
\(V=2\ \text{м}^3\)
\(\rho_{\text{в}}=1000\ \text{кг/м}^3\)
\(\rho_{\text{б}}=2300\ \text{кг/м}^3\)
__________________
\(F_{\text{вода}},\ F_{\text{воздух}}-?\)


В воде на плиту действуют три силы: сила тяжести \(F_{\text{тяж}}=mg=\rho_{\text{б}}Vg\), сила Архимеда \(F_A=\rho_{\text{в}}Vg\) и удерживающая сила \(F_{\text{вода}}\), при этом: \begin{gather*} F_{\text{тяж}}=F_A+F_{\text{вода}}\Rightarrow F_{\text{вода}}=F_{\text{тяж}}-F_A=\rho_{\text{б}}Vg-\rho_{\text{в}}Vg\\[7pt] F_{\text{вода}}=(\rho_{\text{б}}-\rho_{\text{в}})Vg\\[7pt] F_{\text{вода}}=(2300-1000)\cdot 2\cdot 9,8=25480\ (\text{Н})\approx 25,5\ (\text{кН}) \end{gather*} В воздухе на плиту также действуют три силы, но т.к. плотность воздуха в две тысячи раз меньше плотности бетона, выталкивающей силой воздуха можно пренебречь \((F_A\approx 0)\).
Поэтому: \begin{gather*} F_{\text{воздух}}\approx F_{\text{тяж}}=\rho_{\text{б}}Vg\\[7pt] F_{\text{воздух}}=2300\cdot 2\cdot 9,8=45080\ (\text{Н})\approx 45,1\ (\text{кН}) \end{gather*} Ответ: ≈25,5 кН; ≈45,1 кН

Задача 5*. (задача Архимеда) Корона царя Гиерона в воздухе весит 20 Н, а в воде 18,75 Н. Плотность золота 20000 кг/м³. Есть ли в короне примеси?
Предполагая, что к золоту было подмешано серебро, определите массу золота и серебра в короне. Плотность серебра 10000 кг/м³.
Найдите объемные части золота и серебра в короне.

Дано:
\(P=20\ \text{Н}\)
\(P_{\text{вода}}=18,75\ \text{Н}\)
\(\rho_{\text{з}}=20000\ \text{кг/м}^3\)
\(\rho_{\text{с}}=10000\ \text{кг/м}^3\)
__________________
\(\rho,\ m_{\text{з}},\ m_{\text{с}}, \frac{V_{\text{з}}}{V},\ \frac{V_{\text{с}}}{V}-?\)

1) Сила Архимеда, выталкивающая корону из воды: \begin{gather*} F_A=P-P_{\text{вода}}=\rho_{\text{в}}Vg\Rightarrow V=\frac{P-P_{\text{вода}}}{\rho_{\text{в}}g} \end{gather*} Плотность короны: \begin{gather*} \rho=\frac mV=\frac{P}{gV}=\frac Pg\cdot \frac{\rho_{\text{в}}g}{P-P_{\text{вода}}}=\frac{P}{P-P_{\text{вода}}}\rho_{\text{в}}\\[6pt] \rho=\frac{20}{20-18,75}\cdot 1000=16000\ \left(\frac{\text{кг}}{\text{м}^3}\right)\lt \rho_{\text{з}} \end{gather*} Плотность меньше плотности золота, значит, в короне ей примеси.
2) Масса короны: \begin{gather*} m=\rho V=\rho_{\text{з}}V_{\text{з}}+\rho_{\text{с}}V_{\text{с}}=\rho_{\text{з}}V_{\text{з}}+\rho_{\text{с}}(V-V_{\text{з}})\\[6pt] \rho V-\rho_{\text{с}}V=\rho_{\text{з}}V_{\text{з}} -\rho_{\text{с}}V_{\text{з}}\Rightarrow V(\rho-\rho_{\text{с}})=V_{\text{з}}(\rho_{\text{з}}-\rho_{\text{с}})\Rightarrow V_{\text{з}}=\frac{\rho-\rho_{\text{с}}}{\rho_{\text{з}}-\rho_{\text{с}}}V \end{gather*} Масса золота: \begin{gather*} m_{\text{з}}=\rho_{\text{з}}V_{\text{з}}= \frac{\rho-\rho_{\text{с}}}{\rho_{\text{з}}-\rho_{\text{с}}}\rho_{\text{з}}V \end{gather*} Объем короны: \begin{gather*} V=\frac{P-P_{\text{вода}}}{\rho_{\text{в}}g}\approx \frac{20-18,75}{1000\cdot 10}=1,25\cdot 10^{-4}\ (\text{м}^3) \end{gather*} Часть объема золота: \begin{gather*} \frac{V_{\text{з}}}{V}=\frac{\rho-\rho_{\text{с}}}{\rho_{\text{з}}-\rho_{\text{с}}}=\frac{16000-10000}{20000-10000}=0,6=60\ \text{%} \end{gather*} Часть объема серебра: \begin{gather*} \frac{V_{\text{с}}}{V}=100\ \text{%}-60\ \text{%}=40\ \text{%} \end{gather*} Масса короны: \begin{gather*} m=\rho V=16000\cdot 1,25\cdot 10^{-4}=2\ (\text{кг}) \end{gather*} Масса золота: \begin{gather*} m_{\text{з}}=\frac{16000-10000}{20000-10000}\cdot 20000\cdot 1,25\cdot 10^{-4}=1,5\ (\text{кг}) \end{gather*} Масса серебра: \begin{gather*} m_{\text{с}}=m-m_{\text{з}}=2-1,5=0,5\ (\text{кг}) \end{gather*} Ответ: \(\rho=16000\ \frac{\text{кг}}{\text{м}^3};\ m_{\text{з}}=1,5\ \text{кг};\ m_{\text{с}}=0,5\ \text{кг};\ \frac{V_{\text{з}}}{V}=60\ \text{%};\ \frac{V_{\text{с}}}{V}=40\ \text{%}\)

п.6. Лабораторная работа №11. Определение плотности твердых тел и жидкостей методом гидростатического взвешивания

Цель работы
Научиться определять плотности твердых тел и жидкостей методом гидростатического взвешивания.

Теоретические сведения

1) На тело, погруженное в воду, действует выталкивающая сила $$ F_A=\rho_{\text{в}}V_{\text{т}}g $$ где \(\rho_{\text{в}}\) - плотность воды, \(V_{\text{т}}\) - объем тела (части тела), погруженного в жидкость, \(g\) - ускорение свободного падения.

Если вес твердого тела в воздухе \(P=\rho_{\text{т}}V_{\text{т}}g\), его вес в воде \(P=P_{\text{в}}-F_A\)

Отношение веса в воздухе и выталкивающей силы $$ \frac{P}{F_A}=\frac{\rho_{\text{т}}V_{\text{т}}g}{\rho_{\text{в}}V_{\text{т}}g}=\frac{\rho_{\text{т}}}{\rho_{\text{в}}} $$

Плотность тела $$ \rho_{\text{т}}=\frac{P}{F_A}\rho_{\text{в}} $$

Определение плотности твердого тела методом гидростатического взвешивания
Шаг 1. Измерить вес тела в воздухе \(P\)
Шаг 2.. Измерить вес тела в воде \(P_{\text{в}}\).
Шаг 3.. Найти \(F_A=P-P_{\text{в}}\).
Шаг 4.. Найти \(\rho_{\text{т}}=\frac{P}{F_A}\rho_{\text{в}}\).

Найдем погрешность результата.

При использовании динамометра с ценой деления \(d=0,1\ \text{Н}\) абсолютная погрешность прямого измерения веса \(P\) и \(P_{\text{в}}:\ \Delta=\frac d2=0,05\ \text{Н}\).

Абсолютная погрешность вычисления разности \(F_A:\ \Delta_{F_A}=\Delta +\Delta = 2\Delta =d=0,1\ \text{Н}\).

Абсолютную погрешность для табличного значения плотности воды принимаем равной \(\Delta_{\rho_{\text{в}}}=5\ \text{кг/м}^3\).

Из формулы для плотности тела получаем относительную погрешность результата $$ \delta_{\rho_{\text{т}}}=\delta_P+ \delta_{F_A}+\delta_{\rho_{\text{в}}} $$ Где относительные погрешности в сумме вычисляются как обычно.

2) Пусть вес твердого тела в воздухе \(P=\rho_{\text{т}}V_{\text{т}}g\), его вес в воде \(P_{\text{в}}=P-F_{\text{Ав}}\), а вес в другой жидкости \(P_\text{ж}=P-F_{\text{Аж}}\).

Отношение выталкивающих сил в воде и другой жидкости $$ \frac{F_{\text{Ав}}}{F_{\text{Аж}}}=\frac{\rho_{\text{в}}V_{\text{т}}g}{\rho_{\text{ж}}V_{\text{т}}g}=\frac{\rho_{\text{в}}}{\rho_{\text{ж}}} $$

Плотность другой жидкости $$ \rho_{\text{ж}}=\frac{F_{\text{Аж}}}{F_{\text{Ав}}}\rho_{\text{в}} $$

Определение плотности жидкости методом гидростатического взвешивания
Шаг 1. Измерить вес тела в воздухе \(P\)
Шаг 2.. Измерить вес тела в воде \(P_{\text{в}}\).
Шаг 3.. Измерить вес тела в другой жидкости \(P_{\text{ж}}\).
Шаг 4.. Найти \(F_{\text{Ав}}=P-P'_{\text{в}},\ \ F_{\text{Аж}}=P-P'_{\text{ж}}\).
Шаг 5.. Найти \(\rho_{\text{ж}}=\frac{F_{\text{Аж}}}{F_{\text{Ав}}}\rho_{\text{в}}\).

Найдем погрешность результата.

Абсолютная погрешность вычисления разностей \(F_{\text{Ав}},\ F_{\text{Аж}}:\ \Delta_{F}=d=0,1\ \text{Н}\).

Абсолютную погрешность для табличного значения плотности воды принимаем равной \(\Delta_{\rho_{\text{в}}}=5\ \text{кг/м}^3\).

Из формулы для плотности тела получаем относительную погрешность результата $$ \delta_{\rho_{\text{ж}}}= \delta_{F_{\text{Ав}}} + \delta_{F_{\text{Аж}}}+\delta_{\rho_{\text{в}}} $$ Где относительные погрешности в сумме вычисляются как обычно.

Приборы и материалы
Динамометр, тело с подвесом, сосуд с водой, поваренная соль.

Ход работы
1. Измерьте вес тела в воздухе и в воде с помощью динамометра.
2. Найдите \(F_A\), рассчитайте плотность тела \(\rho_\text{т}\). По таблице плотностей определите, из какого вещества состоит тело.
3. Найдите относительную и абсолютную погрешность определения \(\rho_\text{т}\)
4. Добавьте в воду соль из расчета примерно 0,5-0,7 столовой ложки на каждые 100 г воды.
5. Измерьте вес тела в растворе соли с помощью динамометра.
6. Найдите \(F_{\text{Aж}}\), рассчитайте плотность раствора \(\rho_\text{ж}\). По таблице плотностей определите концентрацию \(\mathrm{NaCl}\) в воде.
7. Найдите относительную и абсолютную погрешность определения \(\rho_\text{ж}\).
8. Сделайте выводы.

Результаты измерений и вычислений

1. Определение плотности твердого тела методом гидростатического взвешивания
Вес тела в воздухе \(P=7,3\ \text{Н}\)
Вес тела в воде \(P_{\text{в}}=4,6\ \text{Н}\)
Сила Архимеда в воде \(F_A=P-P_{\text{в}}=7,3-4,6=2,7\ \text{Н}\)
Плотность тела $$ \rho_{\text{т}}=\frac{P}{F_A}\rho_{\text{в}}=\frac{7,3}{2,7}\cdot 1000\approx 2700\ \text{кг/м}^3 $$ Вещество: алюминий

Относительная погрешность \begin{gather*} \delta_{\rho_{\text{т}}}=\delta_P+ \delta_{F_A}+\delta_{\rho_{\text{в}}}= \frac{\Delta}{P}+\frac{2\Delta}{F_A}+\frac{\Delta_{\rho_{\text{в}}}}{\rho_{\text{в}}}=\frac{0,05}{7,3}+\frac{0,1}{2,7}+\frac{5}{1000}\approx \\[6pt] \approx 0,007+0,037+0,005=0,049=4,9\text{%} \end{gather*} Абсолютная погрешность \begin{gather*} \Delta_{\rho_{\text{т}}}= \delta_{\rho_{\text{т}}}\cdot \rho_{\text{т}}=0,049\cdot 2700\approx 130\ \text{кг/м}^3\\[7pt] \rho_{\text{т}}=(2700\pm 130)\ \text{кг/м}^3 \end{gather*}

2. Определение плотности жидкости методом гидростатического взвешивания
Вес тела в воздухе \(P=7,3\ \text{Н}\)
Вес тела в воде \(P_{\text{в}}=4,6\ \text{Н}\)
Вес тела в растворе \(P_{\text{ж}}=4,4\ \text{Н}\)
Сила Архимеда в воде \(F_{\text{Ав}}=P-P_{\text{в}}=7,3-4,6=2,7\ \text{Н}\)
Сила Архимеда в растворе \(F_{\text{Аж}}=P-P_{\text{ж}}=7,3-4,4=2,9\ \text{Н}\)
Плотность раствора $$ \rho_{\text{ж}}=\frac{F_{\text{Аж}}}{F_{\text{Ав}}}\rho_{\text{в}}=\frac{2,9}{2,7}\cdot 1000\approx 1130\ \text{кг/м}^3 $$ По таблице плотности растворов \(\mathrm{NaCl}\) концентрация раствора \(c=16\text{%}\).

Относительная погрешность \begin{gather*} \delta_{\rho_{\text{ж}}}= \delta_{F_{\text{Ав}}}+\delta_{F_{\text{Аж}}}+\delta_{\rho_{\text{в}}}= \frac{2\Delta}{F_{\text{Ав}}}+\frac{2\Delta}{F_{\text{Аж}}}+\frac{\Delta_{\rho_{\text{в}}}}{\rho_{\text{в}}}=\frac{0,1}{2,7}+\frac{0,1}{2,9}+\frac{5}{1000}\approx \\[6pt] \approx 0,037+0,034+0,005=0,076=7,6\text{%} \end{gather*} Абсолютная погрешность \begin{gather*} \Delta_{\rho_{\text{ж}}}= \delta_{\rho_{\text{ж}}}\cdot \rho_{\text{ж}}=0,076\cdot 1130\approx 90\ \text{кг/м}^3\\[7pt] \rho_{\text{ж}}=(1130\pm 90)\ \text{кг/м}^3 \end{gather*}

Выводы
На основании проделанной работы можно сделать следующие выводы.

При определении плотности тела методом гидростатического взвешивания получили $$ \rho_{\text{т}}=(2700\pm 130)\ \text{кг/м}^3 $$ Относительная погрешность результата \(\delta_{\rho_{\text{т}}}=4,9\text{%}\)
Вещество, из которого состоит тело – алюминий.

При определении плотности раствора поваренной соли методом гидростатического взвешивания получили \begin{gather*} \rho_{\text{ж}}=(1130\pm 90)\ \text{кг/м}^3 \end{gather*} Относительная погрешность результата \(\delta_{\rho_{\text{ж}}}=7,6\text{%}\)
По таблице плотности растворов \(\mathrm{NaCl}\) концентрация раствора \(c=16\text{%}\).

Таким образом, все задачи, которые были поставлены перед исследованием, успешно выполнены.