Виды равновесия. Центр тяжести

п.1. Центр тяжести

Если точка опоры (или точка подвеса) совпадает с центром тяжести тела, то тело находится в равновесии.

Примеры центров тяжести тел

Однородный стержень 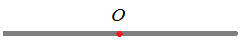Центр тяжести – посредине стержня	Однородный диск 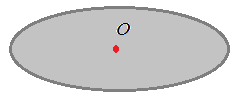Центр тяжести – в центре диска
Однородный прямоугольник 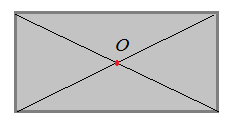Центр тяжести – точка пересечения диагоналей прямоугольника	Однородный треугольник 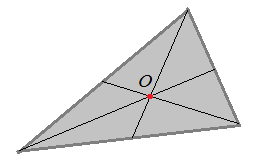Центр тяжести – точка пересечения медиан треугольника

«Однородный» в данных примерах означает, что в телах нет уплотнений или полостей, их плотность везде одинакова.

п.2. Виды равновесия

Для практических задач важно, как поведет себя тело при небольших отклонениях от положения равновесия: вернется в исходное состояние или нет.

С этой точки зрения, различают три вида равновесия.

Устойчивое равновесие	Неустойчивое равновесие	Безразличное равновесие
При малом отклонении от положения равновесия тело возвращается в исходное состояние (шарик скатывается обратно в лунку).	При малом отклонении от положения равновесия тело удаляется от положения равновесия (шарик скатывается с горки).	При малом отклонении от положения равновесия тело остается в равновесии в новом положении (шарик остается на ровном столе в любой его точке).
Шарик возвращается обратно в лунку	Шарик скатывается с горки	Шарик остается неподвижным на ровном столе в любой его точке
Центр тяжести в положении равновесия ниже оси вращения при отклонении.	Центр тяжести в положении равновесия выше оси вращения при отклонении.	Центр тяжести в положении равновесия на оси вращения при отклонении.
Равнодействующая сил при отклонении направлена в сторону положения равновесия.	Равнодействующая сил при отклонении направлена от положения равновесия.	Равнодействующая сил при отклонении равна 0.
При наличии площади опоры, вертикаль, проходящая через центр тяжести при отклонении, пересекает площадь опоры.	При наличии площади опоры, вертикаль, проходящая через центр тяжести при отклонении, не пересекает площадь опоры.	При наличии площади опоры, вертикаль, проходящая через центр тяжести при отклонении, перпендикулярна площади опоры.

п.3. Задачи

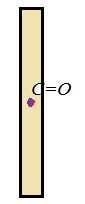
Задача 1. Однородная линейка подвешена на гвозде и находится в состоянии равновесия. Определите тип равновесия для каждого расположения точки подвеса C.

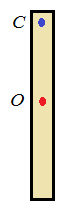
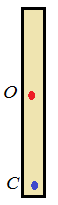
Точка подвеса C совпадает с центром тяжести. При отклонении центр тяжести окажется на оси вращения. Равнодействующая сил будет равна 0. Получаем безразличное равновесие.	Точка подвеса C находится над центром тяжести. При отклонении центр тяжести окажется ниже оси вращения. Равнодействующая сил будет направлена к центру тяжести. Получаем устойчивое равновесие.	Точка подвеса C находится под центром тяжести. При отклонении центр тяжести окажется выше оси вращения. Равнодействующая сил будет направлена от центра тяжести. Получаем неустойчивое равновесие.

Задача 2. Однородный куб лежит на горизонтальной плоскости. На какой угол его нужно приподнять, чтобы опрокинуть через ребро?


На рисунке слева куб лежит на горизонтальной плоскости; сила тяжести \(F_{\text{т}}\) направлена из центра тяжести перпендикулярно вниз, линия её действия проходит через центр площади опоры.

Приподнимем куб на ребре на угол меньше 45°. Линия действия силы тяжести \(F_{\text{т}}\) сдвигается, но по-прежнему проходит через ту же плоскость опоры. Если отпустить куб, он станет вращаться. Ось вращения пройдет вдоль ребра, плечо силы тяжести \(l\) показано на рисунке. Момент силы тяжести направлен против часовой стрелки и вернет куб в исходное положение.

Если приподнять куб на ребре на угол α=45°, линия действия силы тяжести проходит через ребро. Вращающего момента нет, получаем неустойчивое равновесие.

Наконец, если приподнять куб на ребре на угол больше 45°, линия действия силы тяжести выйдет за исходную плоскость опоры. Если отпустить куб, он станет вращаться вокруг ребра. Момент сил тяжести направлен по часовой стрелке и перевернет куб на другую плоскость.
Ответ: на угол больше 45°.

п.4. Лабораторная работа №10. Определение центра тяжести тела

Цель работы
Научиться находить центр тяжести пластины неправильной формы методом подвешивания.

Теоретические сведения

При подвешивании пластины в какой-либо точке она будет поворачиваться до тех пор, пока не придет в положение устойчивого равновесия. В этом положении на нее действуют две силы: сила тяжести \(\overrightarrow{F_{\text{т}}}\), приложенная в центре тяжести и направленная вертикально вниз, и сила упругости \(\overrightarrow{F_{\text{упр}}}\), приложенная в точке подвеса и направленная вертикально вверх. Эти две силы уравновешивают друг друга, а значит, точка подвеса и центр тяжести лежат на одной вертикали. В противном случае, возникал бы момент сил, и пластина продолжила бы вращение, а не находилась бы в равновесии.

Расположение точки подвеса и центра тяжести на одной вертикали используется в методе подвешивания, который реализуется в три этапа:

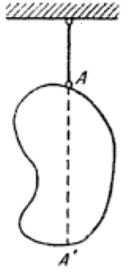	Шаг 1. Подвешиваем пластину в точке A, ждем, пока она придет в равновесие, и с помощью отвеса отмечаем точку A' на нижнем крае пластины.
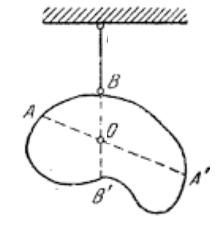	Шаг 2. Подвешиваем пластину в точке B, повторяем всю процедуру и получаем точку B'.
	Шаг 3. Снимаем пластину с подвеса, проводим прямые AA' и BB'. Получаем центр тяжести - точку пересечения O=AA'∩BB'.

Приборы и материалы
Картонная или пластмассовая пластина неправильной формы с тремя отверстиями, штатив, стержень, отвес (нить с грузом), карандаш.

Ход работы

1. Обозначьте отверстия на пластине A,B,C.
2. Закрепите стержень горизонтально в штативе и наденьте на него пластину, используя отверстие A.
3. Аккуратно подвесьте на тот же стержень отвес и отметьте карандашом на пластине точку A' пересечения отвеса и нижнего края пластины.
4. Повторите опыт, надев пластину на стержень через отверстие B.
5. Снимите пластину, проведите линии AA' и BB' и на их пересечении отметьте центр тяжести – точку O=AA'∩BB'.
6. Проведите контрольный опыт, используя отверстие C. Проходит ли отвес через найденный центр тяжести?
7. Сделайте выводы о проделанной работе.

Результаты измерений и вычислений

Для данной пластины были получены следующие прямые, проходящие через центр тяжести.

При подвешивании за третье отверстие C в контрольном опыте вертикальная линия CC' также прошла через точку O - центр тяжести пластины.

Выводы
На основании проделанной работы можно сделать следующие выводы.

Все прямые, проходящие после уравновешивания тела через любую точку подвеса вертикально вниз, пересекаются в одной точке – центре тяжести. На этом основан метод подвешивания.

Метод подвешивания можно использовать для определения центра тяжести тел неправильной формы, а также неоднородных тел (с пустотами или уплотнениями).