Условия плавания тел. Воздухоплавание
На тело, погруженное в жидкость, действует выталкивающая сила $$ F_A=\rho_\text{ж}V_\text{т}g $$ где \(\rho_\text{ж}\) - плотность воды; \(V_\text{т}\) - объем тела (части тела), погруженного в жидкость; \(g\) - ускорение свободного падения (см. §33 данного справочника).
Выталкивающая сила \(F_A\) направлена вертикально вверх, сила тяжести \(V_\text{тяж}\) направлена вертикально вниз. В зависимости от соотношения абсолютных величин этих двух сил, тело будет плавать иди тонуть.

- Если сила тяжести больше архимедовой силы \(F_\text{тяж}\gt F_A\), тело тонет.
- Если сила тяжести меньше архимедовой силы \(F_\text{тяж}\lt F_A\), тело всплывает.
- Если сила тяжести равна архимедовой силе \(F_\text{тяж}=F_A\), и тело полностью погружено в воду, тело плавает на любой глубине.
- Если сила тяжести равна архимедовой силе \(F_\text{тяж}=F_A\), и тело не полностью погружено в воду, тело плавает на поверхности.
В зависимости от соотношения плотности жидкости и плотности тела, получаем:
- Если плотность тела больше плотности жидкости \(\rho_\text{т}\gt \rho_\text{ж}\) тело тонет.
- Если плотность тела меньше плотности жидкости \(\rho_\text{т}\lt \rho_\text{ж}\), тело всплывает и плавает на поверхности. Чем меньше плотность тела по сравнению с плотностью жидкости, тем меньшая часть тела погружена в жидкость.
- Если плотность тела равна плотности жидкости \(\rho_\text{т}=\rho_\text{ж}\), и тело полностью погружено в воду, тело плавает на любой глубине.
п.2. Плавание судов
Чтобы судно держалось на воде, вес воды, вытесняемой подводной частью судна, должен быть равен весу судна с грузом в воздухе или силе тяжести, действующей на судно с грузом: \begin{gather*} F_A=\rho_\text{в}V_\text{подв}g \\[7pt] P=Mg\\[7pt] P=F_A\Leftrightarrow M=\rho_\text{в}V_\text{подв} \end{gather*} В подводной части корабля есть большие полости, поэтому подводная часть имеет большой объем \(V_\text{подв}\), который обеспечивает большую величину выталкивающей силы, достаточную для уравновешивания суммарного веса корабля и груза.
Глубину погружения судна в воду называют осадкой. Поскольку плотность речной воды меньше, чем плотность морской воды, при заходе в реку осадка увеличивается.
Наибольшую допустимую осадку называют ватерлинией; как правило, её отмечают на корпусе красной линией.

Водоизмещение судна – это вес воды, вытесняемой судном с грузом при погружении до ватерлинии, равный силе тяжести, действующей на судно с максимальным допустимым грузом.
п.3. Ареометр
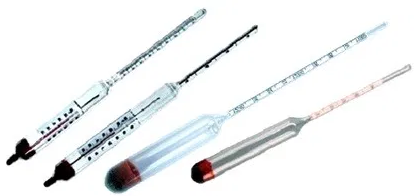 |
Конструктивно ареометр - это поплавок из стекла, который утяжеляется дробью или ртутью. В верхней узкой части находится шкала, которую градуируют в значениях плотности жидкости или концентрации раствора (спиртометр, лактометр, солемер или сахаромер). У ареометров постоянной массы пределы измерений относительно узкие, поэтому на практике используют наборы поплавков. |
Ареометр для жидкостей с плотностью $$ \rho_\text{ж}\lt \rho_\text{воды} $$  |
Ареометр для жидкостей с плотностью $$ \rho_\text{ж}\gt \rho_\text{воды} $$  |
| В этом ареометре метка шкалы 1000 кг/м3 находится внизу. Метки выше показывают 900,800,700 и т.д. кг/м3. В менее плотных жидкостях ареометр будет погружаться больше. |
В этом ареометре метка шкалы 1000 кг/м3 находится вверху. Метки ниже показывают 1100,1200,1300 и т.д. кг/м3. В более плотных жидкостях ареометр будет погружаться меньше. |
п.4. Воздухоплавание
 |
Если наполнить шар газом, плотность которого меньше, чем плотность воздуха, то за счет действия выталкивающей силы можно подняться над поверхностью Земли. Плотность воздуха при \(t=0^\circ C\), \(p=760\ \text{мм рт.ст.}\) $$ \rho_\text{возд}=1,290\ \text{кг/м}^3 $$ При тех же условиях плотность водорода $$ \rho_{\mathrm{H_2}}=0,090\ \text{кг/м}^3, $$ плотность гелия $$ \rho_{\mathrm{He}}=0,179\ \text{кг/м}^3, $$ |
Поскольку \(\rho_{\mathrm{H_2}}\lt \rho_\text{возд}\) и \(\rho_{\mathrm{He}}\lt \rho_\text{возд}\), воздушные шары, наполненные этими газами, будут подниматься наверх в атмосфере; сила Архимеда, действующая на них, будет больше силы тяжести.
 |
Можно также заполнять шар обычным воздухом, только горячим. Плотность воздуха заметно уменьшается с ростом температуры. Например, при \(t=20^\circ C\), \(\rho_\text{возд}=1,205 \text{кг/м}^3\), а при \(t=120^\circ C\), \(\rho_\text{возд}=0,898 \text{кг/м}^3\). С повышением температуры, плотность воздуха внутри шара уменьшается, становится меньшим вес шара, а его подъёмная сила увеличивается. Если хотим подняться наверх, включаем горелку. Если хотим опуститься, выключаем горелку. |
п.5. Задачи
Задача 1. Определите наименьшую площадь плоской льдины толщиной 40 см, способной удержать на себе человека массой 72 кг. Плотность льда 900 кг/м3.
Дано:
\(h=40\ \text{см}=0,4\ \text{м}\)
\(\rho=900\ \text{кг/м}^3\)
\(m=72\ \text{кг}\)
\(\rho_\text{в}=1000\ \text{кг/м}^3\)
__________________
\(S-?\)
Общий вес льдины и человека \begin{gather*} P=(M_\text{л}+m)g=(\rho V+m)g \end{gather*} Объем льдины \(V=Sh\)
При полном погружении льдины в воду на нее будет действовать выталкивающая сила \(F_A=\rho_\text{в}Vg\). Чтобы льдина больше не погружалась, должно выполняться условие \begin{gather*} P=F_A\\[7pt] (\rho V+m)g=\rho_\text{в}Vg\\[7pt] \rho V+m=\rho_\text{в}V\\[7pt] m=(\rho_\text{в}-\rho)V=(\rho_\text{в}-\rho)Sh \end{gather*} Площадь льдины \begin{gather*} S=\frac{m}{(\rho_\text{в}-\rho)h} \end{gather*} Получаем \begin{gather*} S=\frac{72}{(1000-900)\cdot 0,4}=1,8\ (\text{м}^2) \end{gather*} Ответ: 1,8 м2
Задача 2. Найдите вес, архимедову силу и подъемную силу воздушного шара объемом \(V=40\ \text{м}^3\), наполненного гелием. Плотность воздуха \(\rho_\text{возд}=1,29\ \text{кг/м}^3\), плотность гелия \(\rho_{\mathrm{He}}=0,18\ \text{кг/м}^3\); \(g=9,8\ \text{м/с}^2\). Ответы округлите до десятых долей ньютона.
Может ли шар поднять груз весом \(400\ \text{Н}\)?
Дано:
\(\rho_\text{возд}=1,29\ \text{кг/м}^3\)
\(\rho_{\mathrm{He}}=0,18\ \text{кг/м}^3\)
\(g=9,8\ \text{м/с}^2\)
\(P_{\text{гр}}=400\ \text{Н}\)
__________________
\(P,\ F_A,\ F_{\text{под}}-?\)
Вес шара: \begin{gather*} P=mg=\rho_{\mathrm{He}}Vg=0,18\cdot 40\cdot 9,8\approx 70,6\ (\text{Н}) \end{gather*} Архимедова сила, действующая на шар в воздухе: $$ F_A=\rho_\text{возд}Vg=1,29\cdot 40\cdot 9,8\approx 505,7\ (\text{Н}) $$ Подъёмная сила шара: \begin{gather*} F_{\text{под}}=F_A-P=505,7-70,6=435,1\ (\text{Н}) \end{gather*} Вес груза меньше подъемной силы: $$ 400\ \text{Н}\lt 435,1\ \text{Н},\ \ P_{\text{гр}}\lt F_{\text{под}} $$ Шар может поднять этот груз.
Ответ: 70,6 Н; 505,7 Н; 435,1 Н; может
Задача 3. Льдина плавает в пресной воде. Объем ее надводной части 20 м3. Каков объем подводной части? Плотность льда 900 кг/м3.
Дано:
\(\rho=900\ \text{кг/м}^3\)
\(V_\text{над}=20\ \text{м}^3\)
\(\rho_{\text{в}}=1000\ \text{кг/м}^3\)
__________________
\(V_{\text{под}}-?\)
Вес льдины в воздухе: \begin{gather*} P=Mg=\rho Vg=\rho(V_\text{над}+V_{\text{под}})g \end{gather*} Сила Архимеда, действующая на подводную часть: \begin{gather*} F_A=\rho_{\text{в}}V_{\text{под}}g \end{gather*} Силы уравновешивают друг друга \begin{gather*} P=F_A\\[7pt] \rho(V_\text{над}+V_{\text{под}})g= \rho_{\text{в}}V_{\text{под}}g\\[7pt] \rho(V_\text{над}+V_{\text{под}})= \rho_{\text{в}}V_{\text{под}}\\[7pt] (\rho_{\text{в}}-\rho)V_{\text{под}}=\rho V_\text{над} \end{gather*} Объем подводной части \begin{gather*} V_{\text{под}}=\frac{\rho}{\rho_{\text{в}}-\rho}V_\text{над} \end{gather*} Для льда и воды в общем случае \begin{gather*} V_{\text{под}}=\frac{900}{1000-900}V_\text{над}=9V_\text{над} \end{gather*} Объем подводной части льда в воде в 9 раз больше объема надводной части.
В данном случае: $$ V_{\text{под}}=9\cdot 20=180\ (\text{м}^3) $$ Ответ: 180 м3
Задача 4*. Наполненный теплым воздухом воздушный шар объемом 1600 м3 парит на высоте 5,5 км, где плотность воздуха в два раза меньше, чем на уровне моря. Какова плотность воздуха внутри шара, если общая масса его оболочки и груза 150 кг? Ответ округлите до сотых долей кг/м3.
Дано:
\(V=1600\ \text{м}^3\)
\(\rho=\frac 12\rho_0\)
\(M=150\ \text{кг}\)
\(\rho_0=1,29\ \text{кг/м}^3\)
__________________
\(\rho_{\text{ш}}-?\)
Масса шара – сумма массы оболочки с грузом и воздуха внутри: \begin{gather*} M_{\text{ш}}=M+\rho_{\text{ш}}V \end{gather*} Вес шара: \begin{gather*} P=M_{\text{ш}}g=(M+\rho_{\text{ш}}V)g \end{gather*} Выталкивающая сила на данной высоте \begin{gather*} F_A=\rho Vg=\frac 12\rho_0 Vg \end{gather*} Условие равновесия \begin{gather*} P=F_A\\[6pt] (M+\rho_{\text{ш}}V)g=\frac 12\rho_0 Vg\\[6pt] M+\rho_{\text{ш}}V=\frac 12\rho_0 V\\[6pt] \rho_{\text{ш}}V=\frac 12\rho_0 V-M \end{gather*} Плотность воздуха в шаре \begin{gather*} \rho_{\text{ш}}=\frac 12\rho_0-\frac MV \end{gather*} Получаем \begin{gather*} \rho_{\text{ш}}=\frac 12\cdot 1,29-\frac{150}{1600}\approx 0,55\ \text{кг/м}^3 \end{gather*} Ответ: ≈55 кг/м3
Задача 5*. Льдинка плавает на границе между водой и керосином. Какая часть её объема находится ниже этой границы, если керосин покрывает льдинку полностью?
Дано:
\(\rho_1=800\ \text{кг/м}^3\)
\(\rho_2=1000\ \text{кг/м}^3\)
\(\rho=900\ \text{кг/м}^3\)
__________________
\(\frac{V_\text{под}}{V}-?\)
Пусть высота слоя керосина над границей с водой равна \(h_1\), высота льдинки над границей равна \(h_\text{над}\), высота льдинки под границей равна \(h_\text{под}\).
Сверху на льдинку действует сила \(F_1\), которая равна давлению столба керосина высотой \(h_1-h_\text{над}\) на площадь верхней поверхности льдинки: \begin{gather*} F_1=\rho g(h_2-h_\text{над})S. \end{gather*} Снизу по закону Паскаля на льдинку действует сила \(F_2\), которая равна сумме давлений всего столба керосина высотой \(h_1\) и столба воды высотой \(h_\text{под}\) на площадь нижней поверхности льдинки: \begin{gather*} F_2=\rho_1 gh_1S+\rho_2gh_\text{под}S. \end{gather*} На любом промежуточном уровне силы, действующие на боковые поверхности, равны по значению и противоположны по направлению, т.е. взаимно уравновешивают друг друга.
Равнодействующая всех сил, действующих на тело со стороны жидкости, является выталкивающей силой и равна: \begin{gather*} F_A=F_2-F_1=\rho_1gh_1S+\rho_2gh_\text{под}S-\rho_1g(h_1-h_\text{над})S=\\[7pt] =(\rho_1H_1\rho_2h_\text{под}-\rho_1h_1+\rho_1h_\text{над})gS=(\rho_1h_\text{над}+\rho_2h_\text{под})gS=\\[7pt] =(\rho_1V_\text{над}+\rho_2V_\text{под})g \end{gather*} Учитывая, что \(V_\text{над}=V-V_\text{под}\), получаем \begin{gather*} F_A\left(\rho_1(V-V_\text{под})+\rho_2V_\text{под}\right)g=\left(\rho_1V+(\rho_2-\rho_1)V_\text{под}\right)g \end{gather*} Вес льдинки \(P=\rho Vg\). Условие равновесия \begin{gather*} P=F_A\\[7pt] \rho Vg=\left(\rho_1V+(\rho_2-\rho_1)V_\text{под}\right)g\\[7pt] \rho V=\rho_1V+(\rho_2-\rho_1)V_\text{под}\\[7pt] (\rho-\rho_1)V=(\rho_2-\rho_1)V_\text{под} \end{gather*} Часть объема льдинки под границей между керосином и водой: \begin{gather*} \frac{V_\text{под}}{V}=\frac{\rho-\rho_1}{\rho_2-\rho_1} \end{gather*} Подставляем: \begin{gather*} \frac{V_\text{под}}{V}=\frac{900-800}{1000-800}=\frac 12 \end{gather*} Под границей находится половина льдинки.
Ответ: 1/2
п.6. Лабораторная работа №12. Изучение условий плавания тела в жидкости
Цель работы
Изучить условия плавания тел в жидкости.
Теоретические сведения
Выталкивающая сила \(F_A\) направлена вертикально вверх, сила тяжести \(F_\text{тяж}\) направлена вертикально вниз. В зависимости от соотношения абсолютных величин этих двух сил, тело будет плавать иди тонуть.
Выталкивающая сила в работе определяется весом вытесненной телом воды.
Чтобы определить этот вес, отметьте уровни воды в измерительном цилиндре до погружения тела в воду и после погружения. Разность уровней даст вам объем вытесненной телом воды \(V_\text{т}\), по которому находится \(F_A=\rho_\text{в}V_\text{т}g\).
Масса тела \(m\) определяется взвешиванием. Вес рассчитывается по формуле \(P=mg\).
Значение \(g\) в работе можно принять \(g\approx 10\ \text{м/с}^2\).
Приборы и материалы
Весы с разновесами, измерительный цилиндр, пробирка-поплавок с пробкой, сухой песок, сухая ткань.
Ход работы
1. Насыпьте в пробирку песка так, чтобы она в мерном цилиндре плавала вертикально, и часть ее была над водой.
2. Отметьте уровни воды в измерительном цилиндре до погружения пробирки в воду \((V_1)\) и после погружения \((V_2)\). Найдите объем вытесненной пробиркой воды \(V_\text{т}=V_2-V_1\).
3. Выньте пробирку из воды, тщательно протрите ее сухой тканью. Определите взвешиванием массу пробирки с точностью до 1 г.
4. Рассчитайте выталкивающую силу и вес пробирки, занесите данные в таблицу.
5. Насыпьте в пробирку еще немного песка и повторите процедуру, начиная с п.2. Проделайте так несколько раз, пока пробирка не утонет.
6. Сделайте выводы об условиях плавания тел в жидкости.
Результаты измерений и вычислений
| № опыта | V1, мл | V2, мл | Vт, мл | m, г | FA, мН | P, мН | Поведение пробирки |
| 1 | 200 | 234 | 34 | 34 | 340 | 340 | \(F_A=P\) плавает на поверхности, выступает на 1/3 |
| 2 | 200 | 245 | 45 | 45 | 450 | 450 | \(F_A=P\) плавает на поверхности, выступает на 1/5 |
| 3 | 200 | 254 | 54 | 54 | 540 | 540 | \(F_A=P\) плавает на любой глубине |
| 4 | 200 | 254 | 54 | 67 | 540 | 670 | \(F_A\lt P\) тонет |
$$ 1\ \text{мл}=10^{-3}\ \text{л}=10^{-3}\ \text{дм}^3=10^{-6}\ \text{м}^3 $$
Вычисления для первого опыта: \begin{gather*} F_A=\rho_\text{в}V_\text{т}g=1000\cdot 34\cdot 10^{-6}\cdot 10=340\cdot 10^{-3}\ (\text{Н})=340\ (\text{мН})\\[7pt] P=mg=34\cdot 10^{-3}\cdot 10=340\cdot 10^{-3}\ (\text{Н})=340\ (\text{мН}) \end{gather*} Вычисления для остальных опытов проводятся аналогично.
Выводы
На основании проведенных экспериментов можно сделать следующие выводы.
Если вес равен архимедовой силе \(P=F_A=540\ \text{мН}\), пробирка полностью погружена в воду и плавает на любой глубине. Средняя плотность пробирки при этом равна плотности воды.
Если вес равен архимедовой силе \(P=F_A\lt 540\ \text{мН}\), пробирка не полностью погружена в воду, она плавает на поверхности. Чем меньше P, тем большая часть пробирки выступает над водой; тем меньше средняя плотность пробирки по сравнению с плотностью воды.
Если вес больше архимедовой силы \(P\gt F_A=540\ \text{мН}\), пробирка тонет. Её средняя плотность становится больше плотности воды.


