Сообщающиеся сосуды. Гидравлический пресс

п.1. Закон сообщающихся сосудов

Как было показано в §31 данного справочника, давление столба жидкости не зависит от формы или размера дна сосуда. На одном и том же уровне \(h\) давление будет одинаковым.

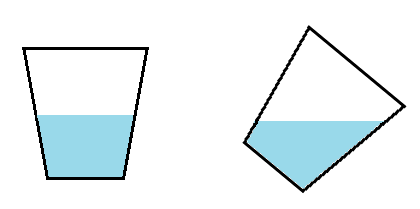
Поэтому, когда жидкость приходит в равновесие, давление выравнивается, и её поверхность становится горизонтальной.

Поверхность покоящейся жидкости всегда горизонтальна

Второй случай с U-образной трубкой представляет значительный практический интерес, поскольку её колена являются так называемыми сообщающимися сосудами.

Из сказанного выше следует, что при любой форме сообщающихся сосудов жидкость, налитая в них, будет перетекать, пока не установится на одном уровне в каждом из колен.

п.2. Сообщающиеся сосуды с различными жидкостями

Теперь рассмотрим, какой уровень установится, если в U-образную трубку налить две несмешивающиеся жидкости с различной плотностью, например, керосин и воду.

На рисунке пунктиром обозначен горизонтальный уровень, который проходит под слоем керосина. На этом уровне в обоих коленах трубки находится вода, а значит, давления по закону Паскаля одинаковы. Можем записать $$ \rho_2gh_2=\rho_1gh_1 \Rightarrow \frac{h_2}{h_1}=\frac{\rho_1}{\rho_2} $$ Получаем если \(\rho_1\gt \rho_2\), то \(h_1\lt h_2\); если \(\rho_1\lt \rho_2\), то \(h_1\gt h_2\); если \(\rho_1=\rho_2\), то \(h_1=h_2\);

п.3. Гидравлический пресс

Закон Паскаля и закон сообщающихся сосудов позволяет создавать гидравлические механизмы с многократным выигрышем в силе.

Гидравлический пресс состоит из двух сообщающихся цилиндрических сосудов разного диаметра. Сосуды заполняются водой, маслом или другой жидкостью. По закону Паскаля давление одинаково по всем направлениям и передается по всему объему.

Если подействовать на меньший поршень слева силой \(F_1\), направленной вниз, под поршнем возникнет избыточное давление \(p=\frac{F_1}{S_1}\). Это давление будет передаваться по всему объему в жидкости, и под большим поршнем справа получим \(p=\frac{F_2}{S_2}\). На большой поршень будет действовать сила \(F_2=pS_2=F_1\frac{S_2}{S_1}\), направленная вверх.

За счет разности площади поршней получаем выигрыш в силе $$ k=\frac{F_2}{F_1}=\frac{S_2}{S_1} $$

Гидравлический пресс был изобретен в 1795 году и с тех пор нашёл множество применений в различных отраслях производства. В современных прессах можно получить силу порядка сотен миллионов ньютонов, что используется для штамповки изделий из металла, прессования картона и хлопка, выдавливания масла из семян и т.д.

п.4. Задачи

Задача 1. Диаметр одного цилиндрического ведра в 1,2 раза больше, чем другого. В оба ведра налили по 5 л воды. В каком ведре давление на дно больше и во сколько раз?

Дано:
\(d_1=1,2=d_2\)
\(V=5\ \text{л}\)
__________________
\(\frac{p_2}{p_1}-?\)

Площадь дна каждого из ведер $$ S_1=\frac{\pi d^2_1}{4},\ \ S_2=\frac{\pi d^2_2}{4} $$ Найдем высоту столба воды в каждом из ведер $$ V=Sh\Rightarrow h_1=\frac{V}{S_1}=\frac{4V}{\pi d^2_1},\ \ h_2=\frac{4V}{\pi d^2_2} $$ Давление на дно в каждом из ведер $$ p_1\rho gh_1=\rho g\cdot\frac{4V}{\pi d^2_1},\ \ p_2\rho gh_2=\rho g\cdot\frac{4V}{\pi d^2_2} $$ Отношение давлений $$ \frac{p_2}{p_1}=\frac{\rho g\cdot \frac{4V}{\pi d^2_2}}{\rho g\cdot \frac{4V}{\pi d^2_1}}=\frac{d^2_1}{d^2_2}=\left(\frac{d_1}{d_2}\right)^2 $$ Давление больше в узком ведре.
Отношение давлений равно отношению квадратов диаметров. $$ \frac{p_2}{p_1}=1,2^2=1,44 $$ Ответ: больше в узком ведре; в 1,44 раза

Задача 2. Горизонтально расположенная труба заполнена водой и имеет два поршня. Площади поршней \(S_1=10\ \text{см}^2,\ S_2=1\ \text{дм}^2\). На поршень \(B\) действует сила \(10\ \text{кН}\). С какой силой нужно действовать на поршень \(A\), чтобы уравновесить силу, действующую на поршень \(B\)?


Дано:
\(S_1=10\ \text{см}^2=0,001\ \text{м}^2\)
\(S_2=1\ \text{дм}^2=0,01\ \text{м}^2\)
\(F_2=10\ \text{кН}=10^4\ \text{Н}\)
__________________
\(F_1-?\)

При действии силы \(F_2\) на поршень \(B\) в воде возникает давление $$ p=\frac{F_2}{S_2}. $$ По закону Паскаля давление передается во все стороны, и у поршня \(A\) получаем $$ p=\frac{F_1}{S_1}. $$ Для уравновешивающей силы $$ \frac{F_1}{S_1}=\frac{F_2}{S_2}\Rightarrow F-1=F_2\frac{S_1}{S_2} $$ Подставляем $$ F_1=10^4\cdot \frac{0,001}{0,01}=10^3\ (\text{Н})=1\ (\text{кН}) $$ Ответ: 1 кН

Задача 3. U-образную трубку частично заполнили водой. В левое колено долили слой керосина высотой 25 см. В каком колене установился уровень выше? Найдите перепад высот \(h\) между уровнями поверхности воды в правом колене и уровнем керосина в левом колене. Ответ запишите в сантиметрах.


Дано:
\(h_2=25\ \text{см}=0,25\ \text{м}\)
\(\rho_1=1000\ \text{кг/м}^3\)
\(\rho_2=800\ \text{кг/м}^3\)
__________________
\(h-?\)

На уровне под слоем керосина в обоих коленах трубки находится вода, а значит, давления на этом уровне по закону Паскаля одинаковы в обоих коленах. Можем записать $$ \rho_2gh_2=\rho_1gh_1\Rightarrow h_1=\frac{\rho_2}{\rho_1}h_2 $$ Поскольку плотность керосина меньше, уровень в левом колене с керосином выше.
Разность уровней \begin{gather*} h=h_2-h_1=h_2-\frac{\rho_2}{\rho_1}h_2\\[7pt] h=\left(1-\frac{\rho_2}{\rho_1}\right)h_2 \end{gather*} Получаем: $$ h=\left(1-\frac{800}{1000}\right)\cdot 0,25=0,05\ (\text{м})=5\ (\text{см}) $$ Ответ: в левом колене с керосином; 5 см

Задача 4*. На дно мензурки налита ртуть и в нее опущен конец стеклянной трубки, запаянной сверху. Поверх ртути в мензурку налили слой воды высотой 25 см.
На какую высоту поднимется ртуть в стеклянной трубке?
Примите для расчетов \(p_\text{атм}=1,013\cdot 10^5\ \text{Па},\ g=9,8\ \text{м/с}^2\)
Ответ укажите в миллиметрах.

На какую высоту поднимется ртуть при тех же условиях, если трубка не запаяна сверху?


Дано:
\(\rho_1=1000\ \text{кг/м}^3\)
\(\rho_2=13600\ \text{кг/м}^3\)
\(h_1=25\ \text{см}=0,25\ \text{м}\)
\(g\approx 9,8\ \text{м/с}^2\)
\(p_\text{атм}=1,013\cdot 10^5\ \text{Па}\)
__________________
\(h_2-?,\ h'_2-?\)

Рассмотрим запаянную трубку. На поверхность ртути, в которую опущен конец трубки, оказывают давление столб воды и атмосфера: $$ p=p_1+p_\text{атм}=\rho_1gh_1+p_\text{атм} $$ Под действием этого давления ртуть в запаянной трубке поднимется на высоту $$ h_2=\frac{p}{\rho_2g}=\frac{\rho_1gh_1+p_\text{атм}}{\rho_2g} $$ Получаем $$ h_2=\frac{1000\cdot 9,8\cdot 0,25+1,013\cdot 10^5}{13600\cdot 9,8}\approx 0,778\ (\text{м})=778\ (\text{мм}) $$ Если трубка будет не запаяна, то при подъеме в ней ртути на нее сверху будет действовать атмосферное давление. Высота подъема \begin{gather*} h'_2=\frac{p-p_\text{атм}}{\rho_2g}=\frac{\rho_1gh_1}{\rho_2g}=\frac{\rho_1}{\rho_2}h_1\\[7pt] h'_2=\frac{1000}{13600}\cdot 0,25\approx 0,018\ (\text{м})=18\ (\text{мм}) \end{gather*} Ответ: 778 мм; 18 мм

Примечание: заметим, что разность \(h_\text{атм}=778-18 = 760\ \text{мм}\) – это нормальное атмосферное давление, измеренное в «миллиметрах ртутного столба» (см. §31 данного справочника). Поэтому \(h_2=h'_2+h_\text{атм}\).

Задача 5. Малый поршень гидравлического пресса под действием силы 500 Н опустился на 9 см. При этом большой поршень поднялся на 3 см.
Какая сила действует на большой поршень со стороны жидкости?

Дано:
\(F_1=500\ \text{Н}\)
\(h_1=9\ \text{см}=0,09\ \text{м}\)
\(h_2=3\ \text{см}=0,03\ \text{м}\)
__________________
\(F_2-?\)

Объем воды, вытесняемый при движении малого поршня вниз: \(V=h_1S_1\).
Жидкости практически несжимаемы, поэтому этот объем должен «прирасти» в цилиндре большого поршня за счет его движения вверх: \(V=h_2S_2\).
Получаем для выигрыша в силе: $$ h_1S_1=h_2S_2\Rightarrow \frac{S_2}{S_1}=\frac{h_1}{h_2} $$ Выигрыш в силе равен отношению длин хода малого и большого поршней.
Выигрывая в силе, мы проигрываем в расстоянии.
Сила, действующая на большой поршень: $$ F_2=F_1\frac{S_2}{S_1}=F_1\frac{h_1}{h_2} $$ Подставляем: $$ F_2=500\cdot \frac{0,09}{0,03}=1500\ (\text{Н})=1,5\ (\text{кН}) $$ Ответ: 1,5 кН

Задача 6. Малый поршень гидравлического пресса площадью 1 м² под действием силы 2 кН опустился на 24 см. Площадь большего поршня 8 м². Найдите вес груза, который был поднят большим поршнем и высоту, на которую он был поднят.


Дано:
\(S_1=1\ \text{м}^2\)
\(F_1=2000\ \text{Н}\)
\(h_1=24\ \text{см}=0,24\ \text{м}\)
\(S_2=8\ \text{м}^2\)
__________________
\(P-?,\ h_2-?\)

Вес груза, который можно поднять с помощью пресса, равен силе \(F_2\), которая действует на большой поршень: $$ P=F_2=F_1\frac{S_2}{S_1} $$ Получаем $$ P=2000\cdot \frac 81=16000\ (\text{Н})=16\ (\text{кН}) $$ Объем воды, вытесняемый при движении малого поршня вниз: \(V=h_1S_1\).
Жидкости практически несжимаемы, поэтому этот объем должен «прирасти» в цилиндре большого поршня за счет его движения вверх: \(V=h_2S_2\).
Следовательно $$ h_1S_1=h_2S_2\Rightarrow h_2=h_1\frac{S_1}{S_2} $$ Получаем \begin{gather*} h_2=0,24\cdot \frac 81=0,03\ (\text{м})=3\ (\text{см}) \end{gather*} Ответ: 16 кН; 3 см

Задача 7*. На дне аквариума лежал камень массой 390 г, полностью погруженный в воду. Когда его убрали, давление воды на дно аквариума уменьшилось на 25 Па. Найдите плотность камня, если длина аквариума 40 см, а ширина 14 см. \((g=9,8\ \text{м/с}^2)\).

Дано:
\(m=390\ \text{г}=0,39\ \text{кг}\)
\(\Delta p=25\ \text{Па}\)
\(a=40\ \text{см}=0,4\ \text{м}\)
\(b=14\ \text{см}=0,14\ \text{м}\)
\(\rho_0=1000\ \text{кг/м}^3\)
\(g=9,8\ \text{м/с}^2\)
__________________
\(\rho-?\)

Лежа на дне, камень занимал в аквариуме некий объем $$ V_\text{к}=\frac{m}{\rho} $$ Остальной объем занимала вода. Их суммарный объем $$ V=V_\text{в}+V_\text{к}=Sh=abh $$ Высота слоя воды в аквариуме с камнем $$ h_1=\frac{V_\text{в}+V_\text{к}}{ab} $$ Давление воды на дно в аквариуме с камнем \begin{gather*} p_1=\rho_0gh_1= \rho_0g\frac{V_\text{в}+V_\text{к}}{ab} \end{gather*} Когда камень забрали, в аквариуме осталась только вода объемом \(V_\text{в}\).
Высота слоя воды в аквариуме без камня $$ h_2=\frac{V_\text{в}}{ab} $$ Давление воды на дно в аквариуме без камня $$ p_2=\rho_0gh_2=\rho_0g\frac{V_\text{в}}{ab} $$ Разность давлений $$ \Delta p=p_1-p_2=\rho_0 g\frac{V_\text{в}+V_\text{к}}{ab}-\rho_0g\frac{V_\text{в}}{ab}=\rho_0g\frac{V_\text{к}}{ab}=\frac{\rho_0g}{ab}\cdot \frac{m}{\rho} $$ Откуда плотность камня $$ \rho=\frac{\rho_0g}{ab}\cdot \frac{m}{\Delta p} $$ Подставляем $$ \rho=\frac{1000\cdot 9,8}{0,4\cdot 0,14}\cdot\frac{0,39}{25}=2730\ (\text{кг/м}^3) $$ Ответ: 2730 кг/м³