Равномерное прямолинейное движение и его скорость

п.1. Равномерное прямолинейное движение

Представим себе автомобиль, который движется по прямой дороге и проходит каждый час по 60 км. Пусть автомобиль движется настолько размеренно, что за каждые полчаса проходит 30 км, каждые четверть часа – 15 км, каждые пять минут – 5 км и т.д. Т.е., за любые равные промежутки времени он преодолевает равные расстояния.

Например, если мы отсчитаем четыре равных промежутка времени, то получим следующую цепочку перемещений:

$$ \overrightarrow{AB}=\overrightarrow{BC}= \overrightarrow{CD}=\overrightarrow{DE} $$ Т.е. «равные расстояния в том же направлении» означают не что иное, как «равные перемещения» (см. §6 данного справочника).
Поэтому можем дать еще одно определение.

п.2. Скорость

Примеры направления вектора скорости при движении различных тел

Действительно, т.к. \(v=|\overrightarrow{v}|=\frac{|\overrightarrow{r}|}{t}\) и \(\overrightarrow{|r|}=s\), получаем, что \(v=\frac st\).

В системе СИ (см. §2 данного справочника) путь измеряется в метрах, а время – в секундах.
Поэтому:

Скорость движения транспорта обычно выражают в км/ч.
Могут встречаться и другие внесистемные единицы, например: мм/с, мм/ч, см/с и т.д.

п.3. Правило перевода км/ч в м/с

Выразим 1 км/ч в метрах в секунду: $$ 1\frac{\text{км}}{\text{ч}}=\frac{1\ \text{км}}{1\ \text{ч}}=\frac{1000\ \text{м}}{3600\ \text{c}}=\frac{1}{3,6} \frac{\text{м}}{\text{с}} $$

Верно также обратное правило:

п.4. Скорость света

Согласно современным представлениям, свет – это поток частиц, которые называют фотонами. В однородной среде фотоны перемещаются прямолинейно и равномерно.

Вакуум – это пространство, в котором нет вещества.
Это теоретическое представление. На практике вакуумом считают пространство, в котором вещество всё-таки есть, но его воздействие так мало, что им можно пренебречь.

Это интересно

Со скоростью света в повседневной жизни мы встречаемся каждый раз, когда используем систему глобального позиционирования – GPS. Всего на орбите в системе GPS находится 32 спутника: 24 основных и 8 резервных. Радиосигналы со спутников системы GPS распространяются со скоростью света. Наш приёмник (телефон, планшет или другой прибор) регистрирует сигналы от нескольких спутников и по разности времени регистрации проводит расчёт места, где мы находимся, с точностью до 5-10 метров.

п.5. Задачи

Задача 1. Какой путь относительно берега проплывет плот за 20 мин, если скорость течения реки равна 1,2 м/с? Выразите путь в километрах.

Дано:
t=20 мин=1200 с
v=1,2 м/с
______________________
s - ?

Путь при равномерном прямолинейном движении: s=vt
Подставляем: s=1,2∙1200=1440 (м)=1,44 (км)
Ответ: 1,44 км

Задача 2. Выразите в метрах в секунду следующие значения скорости:
36 км/ч; 1,8 км/ч; 540 км/ч; 7,2 км/ч

Используем выведенное выше правило перевода (делим на 3,6): \begin{gather*} 36\frac{\text{км}}{\text{ч}}=\frac{36\ \text{м}}{3,6\ \text{c}}=10\frac{\text{м}}{\text{c}}\\ 1,8\frac{\text{км}}{\text{ч}}=\frac{1,8\ \text{м}}{3,6\ \text{c}}=0,5\frac{\text{м}}{\text{c}}\\ 540\frac{\text{км}}{\text{ч}}=\frac{540\ \text{м}}{3,6\ \text{c}}=150\frac{\text{м}}{\text{c}}\\ 7,2\frac{\text{км}}{\text{ч}}=\frac{7,2\ \text{м}}{3,6\ \text{c}}=2\frac{\text{м}}{\text{c}} \end{gather*} Ответ: 10 м/с; 0,5 мс; 150 м/с; 2 м/с

Задача 3. Выразите в километрах в час следующие значения скорости:
10 м/с; 15 м/с; 25 м/с; 8 м/с

Используем выведенное выше правило перевода (умножаем на 3,6): \begin{gather*} 10\frac{\text{м}}{\text{c}}=10\cdot 3,6\frac{\text{км}}{\text{ч}}=36\frac{\text{км}}{\text{ч}}\\ 15\frac{\text{м}}{\text{c}}=15\cdot 3,6\frac{\text{км}}{\text{ч}}=54\frac{\text{км}}{\text{ч}}\\ 25\frac{\text{м}}{\text{c}}=25\cdot 3,6\frac{\text{км}}{\text{ч}}=90\frac{\text{км}}{\text{ч}}\\ 8\frac{\text{м}}{\text{c}}=8\cdot 3,6\frac{\text{км}}{\text{ч}}=28,8\frac{\text{км}}{\text{ч}} \end{gather*} Ответ: 36 км/ч; 54 км/ч; 90 км/ч; 28,8 км/ч

Задача 4. Чемпион мира в беге на 100 метров Усейн Болт пробежал дистанцию за 9,58 секунды. Можно ли сказать, что он бегает быстрее ветра, если скорость умеренного ветра 6 м/с? скорость ураганного ветра 33 м/с? Во сколько раз?

Дано:
s=100 м
t=9,58 с
v_ветер=6 м/с
v_ураган=33 м/с
______________________
\(\frac{v}{v_{\text{ветер}}},\ \frac{v_{\text{ураган}}}{v}\) - ?

Скорость бегуна \(v=\frac st\).
Получаем:
\(v=\frac{100}{9,58}\approx 10,4\ (\text{м/с})\gt v_{\text{ветер}}\)
\(\frac{v}{v_{\text{ветер}}}=\frac{10,4}{6}\approx 1,7\) - скорость бегуна больше скорости умеренного ветра в 1,7 раз.
\(v=10,4\ \text{м/с}\lt v_{\text{ураган}}\)
\(\frac{v_{\text{ураган}}}{v}=\frac{33}{10,4}\approx 3,2\) - скорость бегуна меньше скорости ураганного ветра в 3,2 раза.

Ответ: больше умеренного ветра в 1,7 раз; меньше ураганного ветра в 3,2 раза.

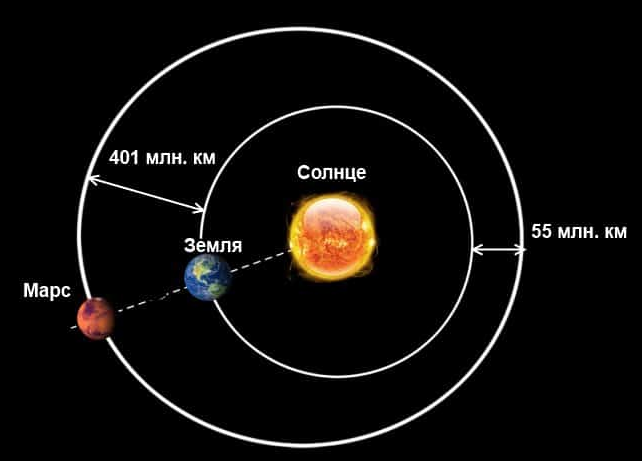
Задача 5. При сближении минимальное расстояние между Землей и Марсом составляет 55 миллиона километров. Сколько времени нужно ждать оператору на Земле, чтобы получить ответ на запрос, отправленный на Марс по каналу связи, если ответ приходит сразу же после получения сигнала? Скорость сигнала равна скорости света.
Сколько придется ждать ответа при максимальном удалении планет на 401 млн.км?

Дано:
s_min=55· 10⁶ км=55· 10⁹ м
c=3· 10⁸ м/с
s_max=401· 10⁶ км=4,01· 10¹¹ м
______________________
t-?

Сигнал посылают с Земли, принимают на Марсе, и оттуда сразу же приходит ответ.
Расстояние в обе стороны составляет 2s. Необходимое время ожидания: \(t=\frac{2s}{c}\)
Получаем: \begin{gather*} t_{min}=\frac{2\cdot 55\cdot 10^9}{3\cdot 10^8}=367\ (c)=6\ \text{мин}\ 7\ \text{c}\\ t_{max}=\frac{2\cdot 4,01\cdot 10^{11}}{3\cdot 10^8}=2673\ (c)=44\ \text{мин}\ 33\ \text{c} \end{gather*}
Ответ: 6 мин 7 с; 44 мин 33 с