Механические волны. Звук и его распространение
п.1. Продольные и поперечные волны
В непрерывной среде колебания одной частицы вызывают колебания соседних частиц, а они, в свою очередь, вызывают колебания других частиц. Так возмущение начинает распространяться, в среде возникают волны.
Подвесим длинную пружину на нитях и ударим по ней слева. Пружина от удара сожмется на определенном участке, а потом этот сжатый участок волной начнет перемещаться слева направо.
 |
Продольные волны всегда приводят к появлению слоев сжатия и разрежения частиц среды. |
Теперь закрепим длинный резиновый шнур одним концом, а другой конец приведем в колебательное движение в вертикальной плоскости. Вертикальные колебания начнут распространяться вдоль шнура, причем в горизонтальном направлении, т.е. перпендикулярно. 
 |
Поперечные волны всегда приводят к сдвигу частиц и слоев среды относительно друг друга. |
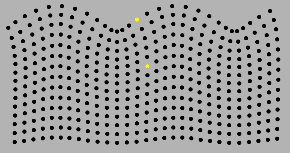 |
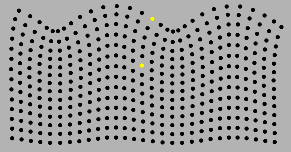 |
Упругие силы при сдвиге слоев возникают только в твердых телах.
Поэтому поперечные волны могут распространяться только в твердых телах.
А вот продольные волны могут распространяться в любых средах: твердых, жидких или газообразных.
п.2. Скорость и длина волны
Длина волны при продольных колебаниях:
Длина волны при поперечных колебаниях:
Частота колебаний определяется источником колебаний, а скорость распространения зависит от свойств среды. Поэтому колебания с одной и той же частотой в разных средах будут распространяться с разной длиной волны.
п.3. Скорость звука, громкость и высота тона
Диапазон частот звуковых волн: от 16-20 Гц до 15-20 кГц.

Звуковая волна связана с перемещением области с небольшим избыточным давлением. Для обычной речи этот избыток составляет всего лишь одну миллионную долю от атмосферного давления.
Скорость звука в воздухе сильнее всего зависит от температуры, меньше – от давления и влажности. При повышении температуры воздуха на 1°С скорость звука в нем увеличивается в среднем на 0,59 м/с.
Скорость звука в воздухе при различной температуре
|
Скорость звука в воде составляет около 1500 м/с и растет с увеличением температуры и солёности (для океанов). Также скорость увеличивается с глубиной.
Скорость звука в твёрдых телах еще выше. Например, в стекле – 3980 м/с, в стали – 5950 м/с, а в алюминии – 6420 м/с.
Как и любая волна, звук характеризуется амплитудой и частотой.
Звуковые волны с большой амплитудой изменения звукового давления мы воспринимаем как громкие (гудок автомобиля), а с малой амплитудой – как тихие звуки (шелест листьев).
Звуковые колебания с высокой частотой мы воспринимаем как звуки высокого тона (писк комара), а колебания с низкой частотой – как звуки низкого тона (жужжание шмеля).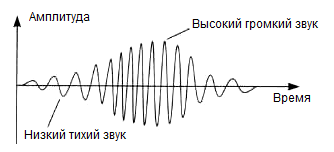
Это интересно
 |
Космос – очень разреженная среда, поэтому обычный звук в том диапазоне волн, которые мы воспринимаем ухом, там распространяться не может. В космосе для нас будет очень тихо . Тем не менее, космос наполнен инфразвуком с очень большой длиной волны (малой частотой колебаний). Ведь продольные волны могут распространяться и в разреженном газе, например, возле звезды, в звездном скоплении или в межзвездных облаках. А источниками служат вспышки сверхновых, столкновения облаков и другие неординарные события. |
п.4. Задачи
Задача 1. Находясь недалеко от скалы, охотник услышал эхо через 4,5 секунды после своего выстрела. На каком расстоянии от охотника находится скала? Считать скорость звука равной 340 м/с.
Дано:
\(t=4,5\ c \)
\(v=340\ м/с\)
__________________
\(s-?\)
За время \(t\) звуковая волна должна достигнуть скалы, отразиться и вернуться обратно.
Пройденный путь: \(2s=vt\)
Расстояние до скалы: \(s=\frac{vt}{2}\)
Получаем: $$ s=\frac{340\cdot 4,5}{2}=765\ (м) $$ Ответ: 765 м
Задача 2. Два последовательных звука слышатся нами раздельно, если пауза между ними длится не менее 0,1 секунды. Каким должно быть минимальное расстояние до преграды, на котором еще можно услышать эхо? Скорость звука считать равной 340 м/с.
Дано:
\(t=0,1\ c \)
\(v=340\ м/с\)
__________________
\(s-?\)
За время \(t\) звуковая волна должна достигнуть преграды, отразиться и вернуться обратно.
Пройденный путь: \(2s=vt\)
Расстояние до преграды: \(s=\frac{vt}{2}\)
Получаем: $$ s=\frac{340\cdot 0,1}{2}=17\ (м) $$ Ответ: 17 м
Задача 3. Контроль качества алюминиевых отливок проводится с помощью генератора ультразвука с частотой 10 МГц. Какая длина волны должна возбуждаться в образце, если скорость звука в качественной отливке равна 6420 м/с.
Дано:
\(f=10\ Мгц=10^7\ Гц\)
\(c=6420\ м/с\)
__________________
\(\lambda-?\)
Длина волны равна произведению скорости волны на период колебаний: $$ \lambda=cT=\frac cf $$ Подставляем: $$ \lambda=\frac{6420}{10^7}=6,42\cdot 10^{-4}\ (м)=642\ (мкм) $$ Ответ: 642 мкм
Задача 4. По озеру проплыл катер. Волна от него до берега дошла за 1,5 мин, расстояние между двумя соседними гребнями волн равно 2 м, а время между двумя последовательными ударами волн о берег – 3 с. Найдите расстояние от берега до катера.
Дано:
\(t=1,5\ мин=90\ с \)
\(\lambda=2\ м \)
\(T=3\ с \)
__________________
\(L-?\)
Скорость распространения волны: $$ v=\frac{\lambda}{T} $$ Расстояние, пройденное волной за время \(t\): $$ L=vt=\frac{\lambda t}{T} $$ Подставляем: $$ L=\frac{2\cdot 90}{3}=60\ (м) $$ Ответ: 60 м
Задача 5*. Скорость звука в чугуне впервые измерил французский ученый Жан-Батист. Он провел следующий опыт: у одного конца пустой чугунной трубы ударяли в колокол; наблюдатель на другом конце трубы слышал два звука, первая звуковая волна пробегала по чугуну, а вторая – по воздуху.
Найдите скорость звука в чугуне, если в опыте Жан-Батиста при длине трубы 931 м промежуток времени между двумя звуками составил 2,5 с. Скорость звука в воздухе примите равной 340 м/с. Ответ округлите до целых.
Дано:
\(L=931\ м\)
\(\triangle t=2,5\ c \)
\(c=340\ м/с \)
__________________
\(v-?\)
Пусть первый звук достиг второго конца трубы через время \(t\). Обе волны, по чугуну и по воздуху, прошли расстояние \(L\): $$ L=vt=c(t+\triangle t) $$ Получаем: \begin{gather*} L=c(t+\triangle t)\Rightarrow t+\triangle t=\frac Lc\Rightarrow t=\frac Lc-\triangle t\\ v=\frac Lt=\frac{L}{\frac Lc-\triangle t} \end{gather*} Подставляем: $$ v=\frac{931}{\frac{931}{340}-2,5}\approx 3908\ (м/c) $$ Ответ: ≈3908 м/с


