Измерение массы и объема. Плотность вещества
п.1. Закон инерции
Как свидетельствуют многочисленные эксперименты и наш повседневный опыт, чтобы неподвижное тело сдвинулось с места, на него должно подействовать другое тело. С другой стороны, чтобы остановить тело, уже находящееся в движении, или изменить его траекторию, также необходимо внешнее воздействие (обычно, причиной остановки в механике является трение; причиной изменения траектории - столкновение с другим телом и т.п.).
Возникает вопрос: а что будет с телом, если на него не действуют никакие другие тела?
Очевидно, если тело покоилось, то оно продолжит покоиться.
А если оно двигалось, что тогда произойдет?
 |
Проведем серию из трёх опытов, в каждом из которых металлический шарик будет скатываться по наклонной плоскости на горизонтальную поверхность. В первом опыте горизонтальная поверхность посыпана песком, во втором – остается чистой, в третьем – покрыта отполированным металлическим листом. В каждом опыте отметим расстояние, пройденное шариком до остановки. Очевидно, что чем меньше трение, тем дальше прокатится шарик, тем дольше он сможет сохранять свою скорость, тем ближе его движение будет к равномерному. |
 |
|
 |
А теперь представим себе идеальный случай: трение полностью отсутствует.
В этом случае шарик будет двигаться с постоянной скоростью бесконечно долго.
Если на тело не действуют другие тела, оно либо покоится, либо движется прямолинейно и равномерно.
Закон инерции впервые был сформулирован Галилео Галилеем в его работе «Диалог о двух главнейших системах мира» (опубликована в 1632 г.). Однако Галилей ошибочно считал, что свободное равномерное движение тела возможно не только по прямой, но и по окружности.
В 1644 г. Рене Декарт уточнил формулировку Галилея, указав, что для изменения направления скорости также необходимо внешнее воздействие. Т.к. при равномерном движении по окружности направление скорости всё время меняется, оно не является свободным. Следовательно, свободное движение может быть только прямолинейным.
п.2. Инертность тела
Благодаря инертности, тело не может мгновенно перейти из состояния покоя в движение или из состояния движения в покой. Для изменения скорости тела необходимо определенное время.
При взаимодействии инертность проявляется в том, что разные тела под одинаковым внешним воздействием получают разные ускорения (об ускорении - см. §11 данного справочника).
п.3. Инертная и гравитационная масса
На сегодняшний день с высоким уровнем точности (относительная ошибка \(\sim 10^{-13}\) в эксперименте 2009 г.) установлено, что значения инертной и гравитационной массы одного и того же тела равны. Поэтому инертную и гравитационную массы на практике не различают (принцип эквивалентности) и рассматривают «просто» массу тела.
Масса является одной из семи основных единиц системы СИ (см. §2 данного справочника).
При изучении очень больших или очень малых физических тел удобней использовать внесистемные единицы массы.
Например, в астрофизике единицей для сравнения масс небесных тел служит масса Солнца, \(M_{\odot}\approx 1,99\cdot 10^{30}\ \text{кг}\). А в физической химии при определении масс атомов и молекул используется атомная единица массы, равная 1/12 массы свободного покоящегося атома углерода, \(1\ \text{а.е.м.}\approx 1,66\cdot 10^{-27}\ \text{кг}\).
п.4. Измерение массы с помощью весов
 Весы равноплечие рычажные лабораторные и наборы гирек к ним |
Вес тела определяется сравнением с весом эталонной массы (гири). Весы находятся в равновесии, если помещенные на их чаши тела одинаково притягиваются к Земле. Чтобы найти массу тела, его кладут на одну чашу весов, а на другую – гири известной массы, пока весы не уравновесятся. Гири граммового набора рекомендуется брать руками в медицинских перчатках, а миллиграммового – пинцетом, чтобы не изменить их массу. Уравновешивание следует начинать с гирь большей массы, а затем переходить к меньшим разновесам, т.к. иначе их может не хватить. |
Шаг 1. Поместить тело для взвешивания на левую чашку весов, а на правую чашку весов поставить гири до полного уравновешивания. Записать полученный результат \(m_1\).
Шаг 2. Переложить тело на правую чашку весов, а гири – на левую. Повторить уравновешивание. Записать полученный результат \(m_2\).
Шаг 3. Найти массу тела как среднее арифметическое $$ m=\frac{m_1+m_2}{2}. $$ Абсолютная погрешность двойного взвешивания – это большая из двух величин $$ \Delta m=max(|m_1-m_2|;\ 0,01\text{%}m) $$ т.к. \(\delta_m=0,01\text{%}\) - относительная погрешность для весов класса точности III.
п.5. Плотность вещества
 |
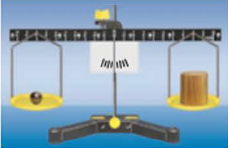 |
| Пластмассовый и деревянный шарики имеют одинаковый объем, но разные массы $$ V_1=V_2=V,\ m_1\lt m_2 $$ $$ \rho_1\lt \rho_2 $$ Плотность пластмассы меньше плотности дерева | Железный шарик и парафиновая свеча имеют одинаковую массу, но разные объемы $$ m_1=m_2=m,\ V_1\lt V_2 $$ $$ \rho_1\gt \rho_2 $$ Плотность железа больше плотности парафина |
| Плотность прямо пропорциональна массе $$ \rho\sim m $$ | Плотность обратно пропорциональна объему $$ \rho\sim \frac 1V $$ |
Плотности различных веществ тщательно измерены и занесены в справочные таблицы.
Плотности в справочнике даны для химически чистых веществ (содержание основного вещества 98% и выше), при нормальных условиях (давление 760 мм рт.ст. и температура 0°С), если не указаны другие значения давления и температуры.
Плотность зависит от следующих свойств вещества:
- масса молекул (атомов) вещества. Например, масса атомов алюминия 27 а.е.м., а атомов золота 197 а.е.м. При этом плотность алюминия 2700 кг/м3, а плотность золота 19300 кг/м3, что приблизительно соответствует соотношению масс атомов. Небольшое различие можно объяснить большим расстоянием между более крупными атомами золота в кристаллической решетке (гранецентрированный куб, как для алюминия, так и для золота).
- расположение частиц вещества. Например, расстояния между слоями атомов углерода в графите в 3 раза больше, чем межатомные расстояния в самих слоях; а вот в алмазе атомы углерода упакованы очень плотно. В результате плотность графита 2160 кг/м3, а плотность алмаза 3510 кг/м3, хотя оба вещества состоят из атомов углерода.
- агрегатное состояние, в котором находится вещество. Наименьшие плотности у газов, наибольшие – у твердых веществ. Например, плотность воздуха (газ) 1,29 кг/м3, плотность воды (жидкость) 1000 кг/м3, плотность железа (твердое тело) 7900 кг/м3.
п.6. Задачи
Задача 1. Найдите плотность мела, если масса кусочка равна 7,2 г, а объем – 3,6 см3.
Дано:
\(m=7,2\ \text{г}=7,2\cdot 10^{-3}\ \text{кг}\)
\(V=3,6\ \text{см}^3=3,6\cdot 10^{-6}\ \text{м}^3\)
__________________
\(\rho-?\)
Плотность \(\rho=\frac mv\) $$ \rho=\frac{7,2\cdot 10^{-3}}{3,6\cdot 10^{-6}}=2\cdot 10^3=2000\ (\text{кг/м}^3) $$ Ответ: \(2000\ \text{кг/м}^3\)
Задача 2. Найдите объем тела человека массой 60 кг, ели средняя плотность человеческого тела равна плотности воды. Ответ дайте в литрах.
Дано:
\(m=60\ \text{кг}\)
\(\rho=1000\ \text{кг/м}^3\)
__________________
\(V-?\)
Плотность \(\rho=\frac mv \Rightarrow\) Объем \(V=\frac mp\) $$ V=\frac{60}{1000}=0,06\ (\text{м}^3)=60\ (\text{л}) $$ Ответ: 60 л.
Задача 3. Алюминиевая кастрюля имеет массу 0,5 кг. Если кастрюлю таких же размеров изготовить из стали, какая у неё будет масса?
Дано:
\(m_1=0,5\ \text{кг}\)
\(\rho_1=2700\ \text{кг/м}^3\)
\(\rho_2=7800\ \text{кг/м}^3\)
__________________
\(m_2-?\)
У кастрюль одинаковых размеров одинаковый объем. Получаем: \begin{gather*} V=\frac{m_1}{\rho_1}=\frac{m_2}{\rho_2}\Rightarrow m_2=\frac{\rho_2}{\rho_1}m_1\\ m_2=\frac{7800}{2700}\cdot 0,5\approx 1,4\ (\text{кг}) \end{gather*} Ответ: ≈1,4 кг.
Задача 4*. В банку, до краев наполненную водой, опустили кусок золота массой 1 кг. В другую такую же банку опустили кусок меди массой 1 кг. Где больше вылилось воды и насколько больше? (ответ дайте в миллилитрах).
Дано:
\(m=1\ \text{кг}\)
\(\rho_1=19320\ \text{кг/м}^3\)
\(\rho_2=8940\ \text{кг/м}^3\)
__________________
\(\Delta V-?\)
Объем вытесненной воды равен объему погруженного тела: $$ V_1=\frac{m}{\rho_1},\ V_2=\frac{m}{\rho_2} $$ Т.к. \(\rho_1\gt \rho_2, V_1\lt V_2\), объем воды, вытесненной медью, больше. $$ \Delta V=V_2-V_1=\frac{m}{\rho_2}-\frac{m}{\rho_1}=m\left(\frac{1}{\rho_2}-\frac{1}{\rho_2}\right)=m\frac{\rho_1-\rho_2}{\rho_1\rho_2} $$ Подставляем: \begin{gather*} \Delta V=1\cdot\frac{19320-8940}{19320\cdot 8940}\approx 6,01\cdot 10^{-5}\ \text{м}^3\\ 1\ \text{л}=10^{-3}\ \text{м}^3,\ \ 1\ \text{мл}=1\ \text{cм}^3=10^{-3}\ \text{л}=10^{-6}\ \text{м}^3\\ \Delta V\approx 60,1\ \text{мл} \end{gather*} Ответ: ≈60,1 мл; больше вылилось во втором случае, для меди.
п.7. Лабораторная работа №5. Определение плотности жидкостей
Цель работы
Научиться измерять массу и объем жидкостей. Научиться определять жидкости по плотности, оценивать погрешность полученных результатов.
Теоретические сведения
Для определения массы тел в данной работе используется метод двойного взвешивания (см. выше в данном параграфе).
Масса тела определяется как среднее арифметическое двух взвешиваний на разных чашках весов: $$ m=\frac{m_1+m_2}{2}. $$ Абсолютная погрешность двойного взвешивания – это большая из двух величин $$ \Delta m=max(|m_1-m_2|;\ 0,01\text{%}m) $$ Пусть масса стакана с жидкостью равна \(M\), абсолютная погрешность этого взвешивания \(\Delta M\); масса пустого стакана \(m_{\text{ст}}\), абсолютная погрешность \(\Delta m_{\text{ст}}\). Тогда масса жидкости $$ m=M-m_{\text{ст}} $$ Абсолютная и относительная погрешности определения массы жидкости $$ \Delta m=\Delta M+\Delta m_{\text{ст}},\ \ \delta_m=\frac{\Delta m}{m}\cdot 100\text{%} $$ Мерный цилиндр проградуирован в миллилитрах. Для расчёта плотности жидкости в системе СИ необходимо помнить, что $$ 1\ \text{мл}=1\ \text{cм}^3=10^{-6}\ \text{м}^3 $$ Абсолютная погрешность измерения объема жидкости равна половине цены деления мерного цилиндра $$ \Delta V=\frac d2 $$ Относительная погрешность равна $$ \delta_V=\frac{\Delta V}{V}\cdot 100\text{%}. $$ Плотность жидкости равна $$ \rho=\frac mv. $$ Относительная погрешность результата $$ \delta_{\rho}=\delta_m+\delta_V. $$ Абсолютная погрешность результата $$ \Delta\rho=\rho\cdot \delta_{\rho} $$ Перевод полученных результатов в систему СИ $$ 1\frac{\text{г}}{\text{см}^3}= \frac{10^{-3}\ \text{кг}}{10^{-6}\ \text{м}^3}=10^3\frac{\text{кг}}{\text{м}^3}=1000\frac{\text{кг}}{\text{м}^3} $$
Приборы и материалы
Два стакана с неизвестными жидкостями; мерный цилиндр; весы с разновесом.
Ход работы
1. Приготовьте весы к взвешиванию.
2. Поставьте на весы первый стакан с жидкостью. Методом двойного взвешивания определите массу стакана и жидкости \(M_1\). Оцените абсолютную погрешность взвешивания.
3. Вылейте жидкость из первого стакан в мерный цилиндр и определите её объем \(V_1\). Оцените абсолютную погрешность измерения объема.
4. Методом двойного взвешивания определите массу первого стакана \(m_{\text{ст1}}\). Оцените абсолютную погрешность взвешивания.
5. По формулам, данным в теоретической части, определите плотность жидкости, относительную и абсолютную погрешности полученного результата.
6. По таблице в справочнике определите, какая жидкость находится в первом стакане.
7.-11. Повторите шаги 2.-6. для второго стакана с жидкостью.
12. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
Цена деления мерного цилиндра \(d=1\ \text{мл}=1\ \text{см}^3\)
Первый стакан
| Стадии двойного взвешивания | \(M,\ \text{г}\) | \(m_{\text{ст}},\ \text{г}\) |
| \(m_1\) | 151,2 | 50,1 |
| \(m_2\) | 150,8 | 49,9 |
| \(m=\frac{m_1+m_2}{2}\) | 151,0 | 50,0 |
| \(|m_1-m_2|\) | 0,4 | 0,2 |
| \(0,01\text{%}m\) | 0,015 | 0,005 |
| \(\Delta m\) | 0,4 | 0,2 |
Масса первой жидкости
\begin{gather*} m=151,0-50,0=101,0,\\ \Delta m=0,4+0,2=0,6,\\ \delta_m=\frac{0,6}{101,0}\cdot 100\text{%}=0,59\text{%} \end{gather*}Объем первой жидкости
\begin{gather*} V=109\ \text{мл},\\ \Delta V=\frac d2=0,5\ \text{мл},\\ \delta_V=\frac{0,5}{109}\cdot 100\text{%}=0,46\text{%} \end{gather*}Плотность первой жидкости
\begin{gather*} \rho=\frac mV=\frac{101,0}{109}\approx 0,927\frac{\text{г}}{\text{см}^3}=927\frac{\text{кг}}{\text{м}^3},\\ \delta_{\rho}=\delta_m+\delta_V=0,59\text{%}+0,46\text{%}\approx 1,1\text{%},\\ \delta \rho=\rho\cdot\delta_{\rho}=927\cdot 0,011\approx 10\frac{\text{кг}}{\text{м}^3},\\ \rho=(927\pm 10)\frac{\text{кг}}{\text{м}^3},\\ \delta_{\rho}=1,1\text{%} \end{gather*}В первом стакане – подсолнечное масло.
Второй стакан
| Стадии двойного взвешивания | \(M,\ \text{г}\) | \(m_{\text{ст}},\ \text{г}\) |
| \(m_1\) | 100,4 | 50,0 |
| \(m_2\) | 100,2 | 49,9 |
| \(m=\frac{m_1+m_2}{2}\) | 100,3 | 49,95≈50,0 |
| \(|m_1-m_2|\) | 0,2 | 0,1 |
| \(0,01\text{%}m\) | 0,01 | 0,005 |
| \(\Delta m\) | 0,2 | 0,1 |
Масса второй жидкости
\begin{gather*} m=100,3-50,0=50,3,\\ \Delta m=0,2+0,1=0,3,\\ \delta_m=\frac{0,3}{50,3}\cdot 100\text{%}=0,6\text{%} \end{gather*}Объем второй жидкости
\begin{gather*} V=50\ \text{мл},\\ \Delta V=\frac d2=0,5\ \text{мл},\\ \delta_V=\frac{0,5}{50}\cdot 100\text{%}=1,0\text{%} \end{gather*}Плотность второй жидкости
\begin{gather*} \rho=\frac mV=\frac{50,3}{50,0}= 1,006\frac{\text{г}}{\text{см}^3}=1006\frac{\text{кг}}{\text{м}^3},\\ \delta_{\rho}=\delta_m+\delta_V=0,6\text{%}+1,0\text{%}= 1,6\text{%},\\ \delta \rho=\rho\cdot\delta_{\rho}=1006\cdot 0,016\approx 16\frac{\text{кг}}{\text{м}^3},\\ \rho=(1006\pm 16)\frac{\text{кг}}{\text{м}^3},\\ \delta_{\rho}=1,6\text{%} \end{gather*}Во втором стакане – вода.
Выводы
На основании проделанной работы можно сделать следующие выводы.
Для определения плотности жидкости в работе методом двойного взвешивания измерялась масса (стакана с жидкостью и пустого стакана) и объем жидкости в мерном цилиндре.
Результаты для двух данных жидкостей
\begin{gather*} \rho_1=(927\pm 10)\frac{\text{кг}}{\text{м}^3},\ \ \delta_{\rho 1}=1,1\text{%}\\ \rho_2=(1006\pm 16)\frac{\text{кг}}{\text{м}^3},\ \ \delta_{\rho 2}=1,6\text{%} \end{gather*}По таблицам в справочнике было определено, что в первом стакане – растительное масло, а во втором – вода. Полученные результаты также подтверждаются цветом (желтоватый – для масла, прозрачный – для воды) и запахом (характерный запах у масла и отсутствие запаха у воды).
п.8. Лабораторная работа №6. Определение плотности твердых тел
Цель работы
Научиться измерять массу и объем твердых тел неправильной формы. Научиться определять вещества твердых тел по плотности, оценивать погрешность полученных результатов.
Теоретические сведения
Для определения массы тел в данной работе используется метод двойного взвешивания (см. выше в данном параграфе).
Масса тела определяется как среднее арифметическое двух взвешиваний на разных чашках весов: $$ m=\frac{m_1+m_2}{2}. $$ Абсолютная погрешность двойного взвешивания – это большая из двух величин $$ \Delta m=max(|m_1-m_2|;\ 0,01\text{%}m) $$ Относительная погрешность $$ \delta_m=\frac{\Delta m}{m}\cdot 100\text{%} $$ Объем твердого тела неправильной формы определяется с помощью погружения в жидкость.
Пусть объем жидкости в мерном цилиндре до погружения тела \(V_0\), после погружения – \(V'\).
Тогда объем самого тела \(V=V'-V_0\).
Абсолютная погрешность измерения объема равна половине цены деления мерного цилиндра \(\Delta V_0=\frac d2\) для прямого измерения. Для разности двух прямых измерений общая абсолютная погрешность $$ \Delta V=2\Delta V_0=d $$ Относительная погрешность $$ \delta_V=\frac dV\cdot 100\text{%}. $$ Плотность твердого тела равна $$ \rho=\frac mv. $$ Относительная погрешность результата $$ \delta_{\rho}=\delta_m+\delta_V. $$ Абсолютная погрешность результата $$ \Delta\rho=\rho\cdot \delta_{\rho} $$ Перевод полученных результатов в систему СИ $$ 1\frac{\text{г}}{\text{см}^3}= \frac{10^{-3}\ \text{кг}}{10^{-6}\ \text{м}^3}=10^3\frac{\text{кг}}{\text{м}^3}=1000\frac{\text{кг}}{\text{м}^3} $$
Приборы и материалы
Мерный цилиндр, наполненный водой наполовину; два тела неправильной формы из металлов; весы с разновесом.
Ход работы
1. Приготовьте весы к взвешиванию.
2. Методом двойного взвешивания определите массу первого тела. Найдите абсолютную и относительную погрешность взвешивания.
3. С помощью погружения первого тела в жидкость найдите его объем. Абсолютная погрешность равна цене деления мерного цилиндра. Рассчитайте относительную погрешность.
4. По формулам, данным в теоретической части, определите плотность твердого тела, относительную и абсолютную погрешности полученного результата.
5. По таблице в справочнике определите, из какого вещества изготовлено первое тело.
6-9. Повторите шаги 2.-5. для второго твердого тела неправильной формы.
10. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
Цена деления мерного цилиндра \(d=0,5\ \text{мл}=0,5\ \text{см}^3\)
Первое тело
| Стадии двойного взвешивания | \(m,\ \text{г}\) |
| \(m_1\) | 22,34 |
| \(m_2\) | 22,38 |
| \(m=\frac{m_1+m_2}{2}\) | 22,36 |
| \(|m_1-m_2|\) | 0,04 |
| \(0,01\text{%}m\) | 0,002 |
| \(\Delta m\) | 0,04 |
| \(\delta m\) | 0,18% |
| Стадии определения объема | \(V,\ \text{см}^3\) |
| \(V_0\) | 50,0 |
| \(V'\) | 58,5 |
| \(V=V'-V_0\) | 8,5 |
| \(\Delta V=d\) | 0,5 |
| \(\delta_V\) | 5,9% |
Плотность первого тела
\begin{gather*} \rho=\frac mV=\frac{22,36}{8,5}\approx 2,631\frac{\text{г}}{\text{см}^3}=2631\frac{\text{кг}}{\text{м}^3},\\ \delta_{\rho}=\delta_m+\delta_V=0,18\text{%}+5,9\text{%}\approx 6,1\text{%},\\ \delta \rho=\rho\cdot\delta_{\rho}=2631\cdot 0,061\approx 160\frac{\text{кг}}{\text{м}^3},\\ \rho=(2630\pm 160)\frac{\text{кг}}{\text{м}^3},\\ \delta_{\rho}=6,1\text{%} \end{gather*}Первое тело изготовлено из алюминия.
Второе тело
| Стадии двойного взвешивания | \(m,\ \text{г}\) |
| \(m_1\) | 101,21 |
| \(m_2\) | 101,27 |
| \(m=\frac{m_1+m_2}{2}\) | 101,25 |
| \(|m_1-m_2|\) | 0,06 |
| \(0,01\text{%}m\) | 0,005 |
| \(\Delta m\) | 0,06 |
| \(\delta m\) | 0,06% |
| Стадии определения объема | \(V,\ \text{см}^3\) |
| \(V_0\) | 50,0 |
| \(V'\) | 63,0 |
| \(V=V'-V_0\) | 13,0 |
| \(\Delta V=d\) | 0,5 |
| \(\delta_V\) | 3,8% |
Плотность второго тела
\begin{gather*} \rho=\frac mV=\frac{101,25}{13,0}\approx 7,788\frac{\text{г}}{\text{см}^3}=7788\frac{\text{кг}}{\text{м}^3},\\ \delta_{\rho}=\delta_m+\delta_V=0,06\text{%}+3,8\text{%}\approx 3,9\text{%},\\ \delta \rho=\rho\cdot\delta_{\rho}=7788\cdot 0,039\approx 300\frac{\text{кг}}{\text{м}^3},\\ \rho=(7790\pm 300)\frac{\text{кг}}{\text{м}^3},\\ \delta_{\rho}=3,9\text{%} \end{gather*}Второе тело изготовлено из железа.
Выводы
На основании проделанной работы можно сделать следующие выводы.
Для определения плотности твердых металлических тел неправильной формы в работе методом двойного взвешивания измерялась масса тел. Объем определялся методом погружения в мерном цилиндре.
Результаты для двух данных тел
\begin{gather*} \rho_1=(2630\pm 160)\frac{\text{кг}}{\text{м}^3},\ \ \delta_{\rho 1}=6,1\text{%}\\ \rho_2=(7790\pm 300)\frac{\text{кг}}{\text{м}^3},\ \ \delta_{\rho 2}=3,9\text{%} \end{gather*}По таблицам в справочнике было определено, что первое тело изготовлено из алюминия, второе – из железа.


