Давление жидкостей и газов. Закон Паскаля

п.1. Особенности давления жидкостей и газов

Давление жидкостей и газов отличается от давления твердых тел. Причина – в особенностях поведения частиц вещества в разных агрегатных состояниях (см. §16 данного справочника).

В отличие от твердых тел, молекулы жидкостей и газов подвижны.

Жидкость принимает форму сосуда, который предохраняет её от растекания. Поэтому жидкость в сосуде оказывает давление не только на дно, но и на стенки. Верхние слои жидкости давят на нижние, и давление растет с глубиной (с увеличением столба жидкости).

Газ заполняет весь предоставленный ему объем. В закрытом сосуде хаотически движущиеся молекулы газа будут сталкиваться с дном, стенками и крышкой сосуда. Таким образом, газ будет оказывать давление во все стороны: вниз, по бокам и даже вверх.

Давление газа также растет с увеличением высоты столба. Однако за счет малой плотности газов этот рост менее заметен по сравнению с жидкостями. В небольшом сосуде давление газа можно считать постоянным во всем объеме сосуда.

Силы давления в жидкости действуют на дно и стенки перпендикулярно поверхности сосуда. Давление на стенку в нижних слоях заметно больше давления в верхних слоях жидкости.

Силы давления в газе действуют перпендикулярно поверхности на дно, стенки, крышку сосуда. Разность давления в верхних и нижних слоях относительно мала. Давление можно считать постоянным во всем объеме сосуда.

п.2. Закон Паскаля

При давлении на жидкость или газ в определенной области происходит сжатие; расстояние между молекулами становится меньше, начинают сильнее действовать силы отталкивания. В результате молекулы перемещаются из области сжатия с большим давлением в области с меньшим давлением. Это происходит достаточно быстро; например, у кислорода при 0°С средняя скорость молекул 425 м/с, у паров воды - 570 м/с. Поэтому в течение небольшого времени давление в сосуде выравнивается.

Для подтверждения закона Паскаля можно провести следующие эксперименты.

Лабораторный эксперимент	Домашний эксперимент
Оборудование и материалы: металлическая сфера с небольшими отверстиями, равномерно распределенными по поверхности, присоединенная к трубке с поршнем, стакан воды. Наливаем воду в трубку, нажимаем на поршень. Результат: из всех отверстий бьют примерно одинаковые струйки воды.	Оборудование и материалы: плотный полиэтиленовый пакет, круглая резинка, игла, вода. Наливаем воду в пакет, плотно его завязываем с помощью резинки, кладем на стол. Иглой делаем несколько отверстий в разных частях пакета. Сильно нажимаем рукой сверху. Результат: из всех отверстий бьют примерно одинаковые струйки воды.

п.3. Давление столба жидкости

Как было замечено выше, давление жидкостей заметно увеличивается с глубиной. Это объясняется тем, что верхние слои давят на нижние.

Найдем давление столба жидкости высотой \(h\)

Согласно закону Паскаля, давление в жидкости передается во всех направлениях одинаково. Поэтому на данной глубине \(h\) в каждой точке уровня давление будет постоянно.

Рассмотрим сосуд в форме прямоугольного параллелепипеда. Пусть в его основании – прямоугольник с длиной \(a\) и шириной \(b\). Нальем в этот сосуд воду до отметки высотой \(h\). Нас интересует давление воды на дно сосуда. Сила давления на дно направлена вертикально вниз и равна силе тяжести: $$ F=mg=\rho Vg $$ Объем воды в сосуде: $$ V=abh $$

Получаем: $$ F=\rho\cdot abh\cdot g $$ Давление на дно сосуда равно отношению силы давления к площади дна: $$ p=\frac FS=\frac{\rho\cdot abh \cdot g}{ab}=\rho gh $$

Давление не зависит от площади дна, и, следовательно, не зависит от его формы.

Полученное выражение будет справедливо для вертикального столба жидкости высотой \(h\) с любым сечением (квадратным, круглым, треугольным, совершенно фантазийным).

Это интересно

Давление не зависит ни от формы, ни от размеров сечения столба жидкости, зато резко увеличивается с высотой. Это свойство использовал Паскаль, продемонстрировав своим современникам забавный эксперимент. Он взял прочную дубовую бочку, наполнил ее доверху водой, плотно закрыл и вставил очень узкую, но очень длинную трубку (около 4 м). Затем он поднялся на второй этаж и вылил в трубку кружку воды. Бочка тут же …лопнула. Действительно, ведь давление в бочке увеличилось на \(p=1000\cdot 10\cdot 4=40\ \text{кПа}\): её будто «придавило» четырьмя тоннами воды, хотя понадобилась всего лишь кружка. Тем не менее, результат этого фокуса всегда кажется неожиданным.

п.4. Давление столба газа

Газы, как и жидкости, также имеют некоторую плотность. Поэтому, рассматривая давление столба газа по аналогии с жидкостью, можно прийти к тем же результатам.

Понимание того, что газ также оказывает разное давление в разных слоях, возникло не сразу. Это объясняется небольшой плотностью газов по сравнению с жидкостями.

Для иллюстрации рассчитаем давление столба воды и столба воздуха высотой \(h=1\ \text{м}\). Плотность воды \(\rho_\text{воды}=1000\ \text{кг/м}^3\), плотность воздуха при 20°C \(\rho_\text{возд}=1,2\ \text{кг/м}^3\). Получаем: \begin{gather*} p_\text{вода}= \rho_\text{вода}gh\approx 1000\cdot 10\cdot 1=10000\ (\text{Па})\\[7pt] p_\text{возд}= \rho_\text{возд}gh\approx 1,2\cdot 10\cdot 1=12\ (\text{Па}) \end{gather*} Из-за разности в плотности, давление отличается почти в 1000 раз, ведь масса кубометра воды – 1 тонна, а масса кубометра воздуха – всего 1,2 кг.

Поэтому при изучении процессов в небольших сосудах разность в давлении газа в верхних и нижних слоях практически не заметна.

С другой стороны, если рассматривать значительные по высоте «столбы» газов, например, атмосферу планеты, давление становится существенной величиной. Так, на поверхности Земли атмосферное давление составляет около 100 000 (Па). Подробней этот вопрос будет рассмотрен в §31 данного справочника.

В итоге, для открытого сосуда с жидкостью, где на поверхность дополнительно оказывает давление атмосфера, давление жидкости на глубине h равно сумме: $$ p=p_\text{атм}+\rho gh $$

п.5. Задачи

Задача 1. Пятый этаж расположен выше первого на 15 м.
На каком этаже давление в трубах водопровода больше и на сколько?

Дано:
\(h=15\ \text{м}\)
\(p=1000\ \text{кг/м}^3\)
\(g\approx 10\ \text{м/с}^2\)
__________________
\(\Delta p-?\)

Давление в водопроводе на первом этаже $$ p_1=p_\text{внеш}+\rho gh, $$ где \(p_\text{внеш}\) – давление, связанное с действием внешних сил (атмосфера, водонапорная башня, насос и т.п.), второе слагаемое – давление вертикального столба жидкости в трубе в доме.
Давление в водопроводе на пятом этаже \(p_5=p_\text{внеш}\).
Давление больше на первом этаже.
Разность давлений $$ \Delta p=p_1-p_5= p_\text{внеш}+\rho gh -p_\text{внеш}=\rho gh $$ Получаем: $$ \Delta p=1000\cdot 10\cdot 15=150\ 000\ (\text{Па})=150\ (\text{кПа}) $$ Ответ: на первом; на 150 кПа

Задача 2. Давление в трубах водопровода \(4\cdot 10^5\ \text{Па}\). На какую максимальную высоту можно достать струей воды в случае пожара, если подключить оборудование к пожарному гидранту на поверхности земли? Атмосферное давление примите равным \(1\cdot 10^5\ \text{Па}\)

Дано:
\(p=4\cdot 10^5\ \text{Па}\)
\(p_\text{атм}=1\cdot 10^5\ \text{Па}\)
\(p=1000\ \text{кг/м}^3\)
\(g\approx 10\ \text{м/с}^2\)
__________________
\(h-?\)

При подключении на струю воды, направленную вертикально вверх, будет действовать снизу давление водопровода, сверху атмосферное давление.
Под действием разности этих давлений вода может подняться на высоту $$ h=\frac{p-p_\text{атм}}{\rho g} $$ Получаем: $$ h=\frac{(4-1)\cdot 10^5}{1000\cdot 10}=30\ (\text{м}) $$ Ответ: 30 м

Задача 3. Рассчитайте, какую силу давления воды должен выдерживать жесткий водолазный скафандр, предназначенный для глубоководных работ на глубине до 365 м, если общая поверхность скафандра составляет 2,5 м²?
(Плотность морской воды 1010 кг/м³, g=9,8 м/с²). Ответ округлите до меганьютонов.

Дано:
\(\rho=1010\ \text{кг/м}^3\)
\(g=9,8\ \text{м/с}^2\)
\(h=365\ \text{м}\)
\(S=2,5\ \text{м}^2\)
__________________
\(F-?\)

Давление воды на максимальной глубине $$ p=\rho gh $$ Сила давления $$ F=pS=\rho ghS $$ Получаем: $$ F=1010\cdot 9,8\cdot 365\cdot 2,5\approx 9,03\cdot 10^6\ (\text{Н})=9\ (\text{МН}) $$ Ответ: ≈9 МН

Задача 4*. В цилиндрический сосуд налиты ртуть и вода. Общая высота столба жидкости 20 см. Чему равно давление, создаваемое жидкостями на дно сосуда, если:
а) объемы жидкостей одинаковы; б массы жидкостей одинаковы?

Дано:
\(\rho_1=1000\ \text{кг/м}^3\)
\(\rho_2=13600\ \text{кг/м}^3\)
\(H=20\ \text{см}=0,2\ \text{м}\)
\(g\approx 10\ \text{м/с}^2\)
\(\text{а)}\ V_1=V_2;\ \ \text{б)}\ m_1=m_2\)
__________________
\(p-?\)

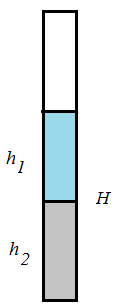а) Рассмотрим столб жидкости с одинаковыми объемами ртути и воды. \begin{gather*} V_1=h_1S,\ \ V_2=h_2S \end{gather*} Поскольку площадь сечения \(S\) одинакова, при одинаковых объемах у столбиков воды и ртути будут одинаковые высоты \begin{gather*} V_1=V_2\Rightarrow h_1=h_2=\frac H2 \end{gather*} Суммарное давление жидкостей на дно сосуда \begin{gather*} p=p_1+p_2=\rho_1 gh_1+\rho_2 gh_2=\rho_1 g\cdot \frac H2+\rho_2 g\cdot \frac H2\\[7pt] p=\frac{\rho_1+\rho_2}{2}gH \end{gather*} Получаем \begin{gather*} p=\frac{1000+13600}{2}\cdot 10\cdot 0,2=14600\ (\text{Па})=14,6\ (\text{кПа}) \end{gather*}

б) Рассмотрим столб жидкости с одинаковыми массами ртути и воды. \begin{gather*} m_1=\rho_1V_1,\ \ m_2=\rho_2V_2\\[7pt] m_1=m_2\Rightarrow \rho_1V_1=\rho_2V_2 \Rightarrow \rho_1h_1S=\rho_2h_2S \Rightarrow \rho_1h_1=\rho_2h_2 \end{gather*} При этом $$ h_1+h_2=H. $$ Подставим $$ h_2=\frac{\rho_1}{\rho_2}h_1 $$ в сумму: \begin{gather*} h_1+\frac{\rho_1}{\rho_2}h_1=H \Rightarrow \left(1+\frac{\rho_1}{\rho_2}\right)h_1=H\\[7pt] h_1=\frac{H}{1+\frac{\rho_1}{\rho_2}}=\frac{\rho_2H}{\rho_1+\rho_2},\\[7pt] h_2=\frac{\rho_1}{\rho_2}h_1=\frac{\rho_1H}{\rho_1+\rho_2} \end{gather*} Суммарное давление жидкостей на дно сосуда \begin{gather*} p=p_1+p_2=\rho_1gh_1+\rho_2gh_2=\rho_1g\cdot\frac{\rho_2H}{\rho_1+\rho_2}+ \rho_2g\cdot\frac{\rho_1H}{\rho_1+\rho_2}\\[7pt] p=\frac{2\rho_1\rho_2}{\rho_1+\rho_2}gH \end{gather*} Получаем \begin{gather*} p=\frac{2\cdot 1000\cdot 13600}{1000+13600}\cdot 10\cdot 0,2\approx 3700\ (\text{Па})=3,7\ (\text{кПа}) \end{gather*}

Ответ: а) 14,6 кПа; б) 3,7 кПа