Степенные функции с целочисленным показателем y=$x^n$

Графики $y = x^3, y = x^4, y = x^5$

Со степенью с натуральным показателем мы уже знакомы

(см. §10 справочника для 7 класса).

С графиком функции y=x² - параболой – мы также уже встречались

(см. §18 справочника для 8 класса).

Построим по точкам графики $y = x^3, y = x^4, y = x^5$ и изобразим все графики в одной системе координат.

Заметим, что при $0 \lt x \lt 1$ выполняется неравенство $x^5 \lt x^4 \lt x^3 \lt x^2$

А при $x \gt 1$ выполняется неравенство $x^2 \lt x^3 \lt x^4 \lt x^5$

Графики степенных функций $y = x^n$ с натуральным показателем

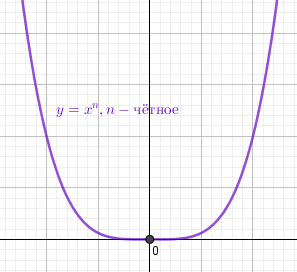
Степенная функция $y = x^n$ с натуральным чётным показателем n убывает на промежутке $(-\infty;0)$ возрастает на промежутке $(0;+ \infty)$ в точке (0;0) - минимум Область определения $x \in \Bbb R$,т.е. $x \in (- \infty;+ \infty)$ Область значений $y \ge 0,т.е.y \in [0;+\infty)$ График симметричен относительно оси Y Функция чётная y(-x) = y(x)
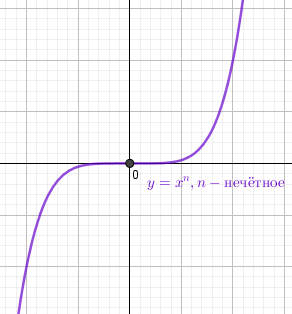
Степенная функция $y = x^n$ с натуральным нечётным показателем n возрастает на всей области определения. Область определения $x \in \Bbb R$,т.е. $x \in (- \infty;+ \infty)$ Область значений $y \in \Bbb R, т.е.y \in [0;+\infty)$ График симметричен относительно начала координат. Функция нечётная y(-x) = -y(x)

Графики функции $y = x^n$ с натуральным показателем называют степенными параболами.

Чаще всего в задачах встречаются $y = x^2$ – «квадратичная парабола» (или, просто «парабола») и $y = x^3$ – «кубическая парабола».

Графики $y=x^{-2}, y = x^{-3},y=x^{-4}$

С графиком $y = x^{-1} = \frac{1}{x}$ - гиперболой - мы уже встречались

(см. §6 справочника для 8 класса).

Построим по точкам графики $y = x^{-2} = \frac{1}{x^2}, y = x^{-3} = \frac{1}{x^3}, y = x^{-4} = \frac{1}{x^4}$ и изобразим все графики в одной системе координат.

Заметим, что при $0 \lt x \lt 1$ выполняется неравенство $ \frac{1}{x} \lt \frac{1}{x^2} \lt \frac{1}{x^3} \lt \frac{1}{x^4} $

А при $x \gt 1$ выполняется неравенство $\frac{1}{x^4} \lt \frac{1}{x^3} \lt \frac{1}{x^2} \lt \frac{1}{x}$

Графики степенных функций $y = x^{-n} = \frac{1}{x^n}$ с целым отрицательным показателем

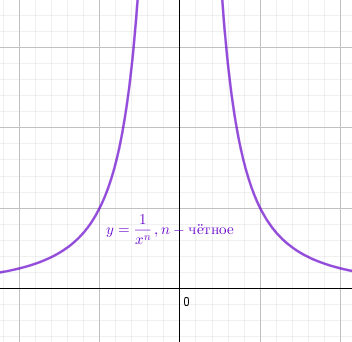
Степенная функция $y = x^{-n} = \frac{1}{x^n}$ с целым отрицательным чётным показателем возрастает на промежутке $(-\infty;0)$ убывает на промежутке $(0;+\infty)$ Область определения $x \neq 0$,т.е. $x \in (-\infty;0) \cup (0;+\infty)$ Область значений $y \gt 0,т.е.y \in (0;+\infty)$ График симметричен относительно оси Y Функция чётная y(-x) = y(x)
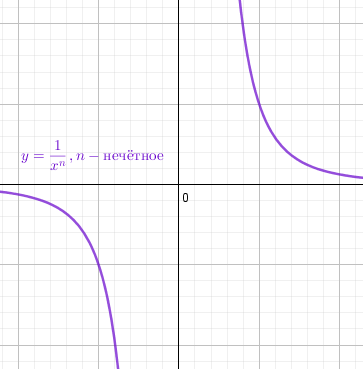
Степенная функция $y = x^{-n} = \frac{1}{x^n}$ с целым отрицательным нечётным показателем убывает на всей области определения. Область определения $x \neq 0$,т.е. $x \in (-\infty;0) \cup (0;+\infty)$ Область значений $y \neq 0, т.е. y \in (-\infty;0) \cup (0;+\infty)$ График симметричен относительно начала координат. Функция нечётная y(-x) = -y(x)

Графики функции $y = x^{-n} = \frac{1}{x^n}$ с отрицательным целым показателем называют степенными гиперболами.

Чаще всего в задачах встречаются $y = x^{-1} = \frac{1}{x}$ – просто «гипербола» и $y = x^{-2} = \frac{1}{x^2}$ – «квадратичная гипербола».

Примеры

Пример 1. Постройте в одной системе координат графики:

$$ y = x^3, \quad y = (x+1)^3, \quad y = x^3-2 $$

Сделайте выводы.

График функции $y = (x+1)^3$ сдвинут на 1 влево по сравнению с графиком $y = x^3$

График функции $y = x^3-2$ сдвинут на 2 вниз по сравнению с графиком $y = x^3$

Пример 2. Постройте в одной системе координат графики:

$$y = x^4, \quad y = -x^4, \quad y = (x-3)^4, \quad y = 2x^4$$

Сделайте выводы.

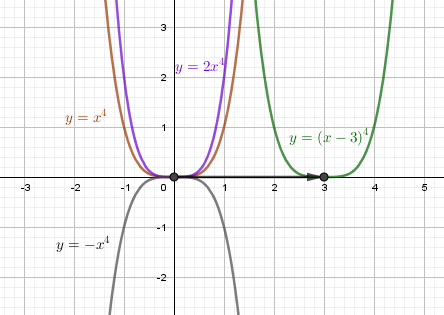
График функции $y = -x^4$ является отражением графика $y = x^4$ относительно оси X

График функции $y = 2x^4$ уже графика $y = x^4$, y растёт быстрее в 2 раза

График функции $y = (x-3)^4$ сдвинут на 3 вправо по сравнению с графиком $y = x^3$

Пример 3. Постройте в одной системе координат графики:

$$ y = \frac{1}{x^2}, \quad y = \frac{1}{(x+2)^2}, \quad y = - \frac{1}{x^2}, \quad y = \frac{1}{x^2}+3 $$

Сделайте выводы.

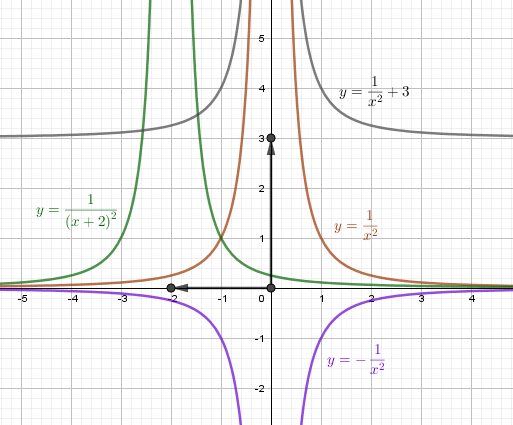
График функции $y = -\frac{1}{x^2}$ является отражением графика $y = \frac{1}{x^2}$ относительно оси X

График функции $y = \frac{1}{(x+2)^2}$ сдвинут на 2 влево по сравнению с графиком $y = \frac{1}{x^2}$

График функции $y = \frac{1}{x^2} +3$ сдвинут на 3 вверх по сравнению с графиком $y = \frac{1}{x^2}$

Пример 4. Решите уравнение графически:

$ а) \frac{1}{x-1} = \frac{x^4}{16} $

Чертим графики $y = \frac{1}{x-1}$ и $y = \frac{x^4}{16}$. Находим точки пересечения:

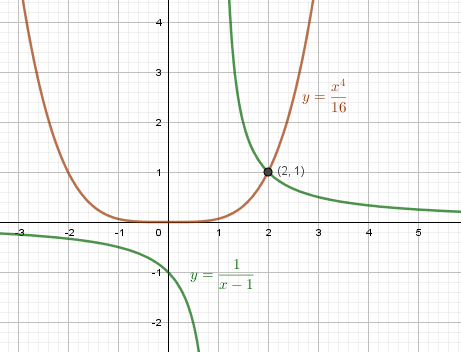
Ответ: x = 2

$ б) \frac{1}{x^3} -x^3 = 0$

$ \frac{1}{x^3} = x^3 $

Чертим графики $y = \frac{1}{x^3}$ и $y = x^3$. Находим точки пересечения:

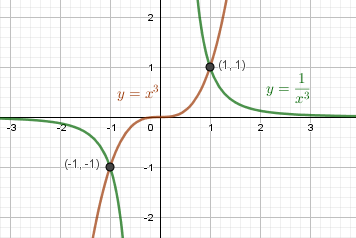
Ответ: $x_{1,2} = \pm1$