Системы уравнений с двумя переменными

п.1. Понятие системы уравнений с двумя переменными и её решения

Например:
\( \left\{ \begin{array}{ l } \mathrm{2x+y=5} & \\ \mathrm{3x-y=5} & \end{array}\right. \)
Пара (2; 1) превращает оба уравнения в верные числовые уравнения:
\( \left\{ \begin{array}{ l } \mathrm{2\cdot 2 + 1 =5} & \\ \mathrm{3\cdot 2-1=5} & \end{array}\right. \)
Ответ: (2; 1).

п.2. Графический метод решения системы уравнений с двумя переменными

Поскольку каждое из уравнений с двумя переменными можно изобразить в виде графика на плоскости, графический метод решения систем таких уравнений достаточно удобен.

Например:

Ответ: (2; 1).

п.3. Примеры

Пример 1. Решите графическим способом систему уравнений:
а) \( \left\{ \begin{array}{ l } \mathrm{x^2+y^2=25} & \\ \mathrm{4x+3y=0} & \end{array}\right. \)
\( \mathrm{x^2+y^2=25} \) – окружность с центром в начале координат
\( \mathrm{4x+3y=0} \) – прямая \( \mathrm{y=-\frac43 x} \)

Система имеет два решения (–3; 4) и (3; –4)
Ответ: {(–3; 4) ; (3; –4)}.

б) \( \left\{ \begin{array}{ l } \mathrm{xy=5} & \\ \mathrm{y-x=4} & \end{array}\right. \)
\( \mathrm{xy=5} \) – гипербола \( \mathrm{y=\frac5x} \)
y – x = 4 – прямая y = x + 4

Система имеет два решения (–5; –1) и (1; 5)
Ответ: {(–5; –1) ; (1; 5)}.

в) \( \left\{ \begin{array}{ l } \mathrm{x^2+y=1} & \\ \mathrm{x^2-y=7} & \end{array}\right. \)
x² + y = 1 – парабола y = –x² + 1
x² – y = 7 – парабола y = x² – 7

Система имеет два решения (–2; –3) и (2; –3)
Ответ: {(–2; –3) ; (2; –3)}.

г) \( \left\{ \begin{array}{ l } \mathrm{xy=1} & \\ \mathrm{x^2+y^2=2} & \end{array}\right. \)
xy = 1 – гипербола \( \mathrm{y=\frac1x} \)
x² + y² = 2 – окружность с центром в начале координат, радиусом \( \mathrm{\sqrt{2}} \)

Система имеет два решения (–1; –1) и (1; 1)
Ответ: {(–1; –1) ; (1; 1)}.

Пример 2*. Решите графическим способом систему уравнений
a) \( \left\{ \begin{array}{ l } \mathrm{x^3-1=1} & \\ \mathrm{\frac1x-y=1} & \end{array}\right. \)
x³ – y = 1 – кубическая парабола y = x³ – 1, смещённая на 1 вниз.
\( \mathrm{\frac1x-y=1} \) – гипербола \( \mathrm{y=\frac1x-1} \), смещённая на 1 вниз

Система имеет два решения (–1; –2) и (1; 0)
Ответ: {(–1; –2) ; (1; 0)}.

б) \( \left\{ \begin{array}{ l } \mathrm{|x|+|y|=2} & \\ \mathrm{x^2+y^2=4} & \end{array}\right. \)
|x| + |y| = 2 – квадрат с диагоналями 4, лежащими на осях
x² + y² = 4 – окружность с центром в начале координат, радиусом 2

Система имеет четыре решения (2; 0), (0; 2) , (–2; 0) и (0; –2)
Ответ: {(2; 0) ; (0; 2) ; (–2; 0) ; (0; –2)}.

в) \( \left\{ \begin{array}{ l } \mathrm{y-x^2=4x+6} & \\ \mathrm{y+|x|=6} & \end{array}\right. \)
y – x² = 4x + 6 – парабола y = (x² + 4x + 4) + 2 = (x + 2)² + 2, ветками вверх, смещённая на 2 влево и на 2 вверх
y + |x| = 6 – ломаная, y = –|x| + 6. Для x > 0, y = –x + 6, для x < 0 – отображение относительно оси OY.

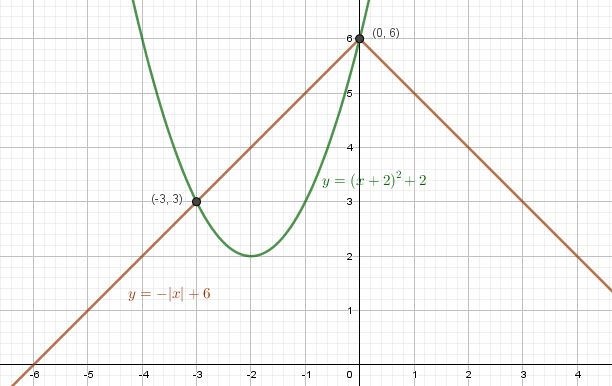
Система имеет два решения (–3; 3) и (0; 6)
Ответ: {(–3; 3) ; (0; 6)}.

г) \( \left\{ \begin{array}{ l } \mathrm{\sqrt{x+2}-y=0} & \\ \mathrm{|x|-y=0} & \end{array}\right. \)
\(\mathrm{\sqrt{x+2}-y=0}\) – ветвь параболы \(\mathrm{y=\sqrt{x+2}}\), смещённая на 2 влево
|x| – y = 0 – ломаная y = |x|.
Для x > 0, y = x, для x < 0 – отображение относительно оси OY.

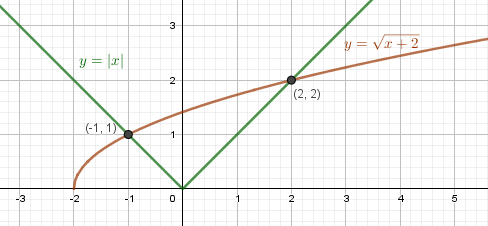
Система имеет два решения (–1; 1) и (2; 2)
Ответ: {(–1; 1) ; (2; 2)}.