Модули в системах уравнений и неравенств с двумя переменными

Подробней о раскрытии модуля в уравнении, см. §40 справочника для 7 класса, а также пример 2 §14 данного справочника.
Подробней о раскрытии модуля в неравенстве, см. §10 данного справочника.

п.1. Примеры

Пример 1. Решите систему уравнений: a) \( \left\{ \begin{array}{ l } \mathrm{|x|+|y|=2} & \\ \mathrm{2y-x^2+4=0} & \end{array}\right. \)
|x| + |y| = 2 – уравнение квадрата с диагоналями длиной 4 на осях координат, точка пересечения диагоналей в начале координат.
\( \mathrm{2y-x^2+4=0\Rightarrow y=\frac{x^2}{2}-2} \) – парабола ветками вверх, с вершиной (0; –2)

Получаем три пары решений.
Ответ: {(–2; 0) (0; –2) (2; 0)}.

б) \( \left\{ \begin{array}{ l } \mathrm{y=|\ |x-1|-1|} & \\ \mathrm{(x-1)^2+y^2=1} & \end{array}\right. \)
Проанализируем первый график:
Исходная прямая y = x – 1 превращается в ломаную y = |x – 1|, «отражается» в точке (1; 0) в положительную полуплоскость y > 0.
Далее, ломаная y = |x – 1| опускается на 1 вниз y = |x – 1| – 1.
Наконец, области y = |x – 1| – 1 с отрицательными Y снова отражаются в положительную полуплоскость y > 0.
Второй график – окружность с центром (1; 0), радиусом 1.

Получаем три пары решений.
Ответ: {(0; 0) (1; 1) (2; 0)}.

Пример 2. Решите графически систему неравенств:
a) \( \left\{ \begin{array}{ l } \mathrm{|x-2|+|y-4|\leq 2} & \\ \mathrm{y\leq \frac{1}{x-2}+4} & \end{array}\right. \)
|x – 2| + |y – 4| ≤ 2 – внутренняя область и стороны квадрата с точкой пересечения диагоналей (2; 4), длиной диагоналей 4.
\( \mathrm{y\leq \frac{1}{x-2}+4} \) – область под гиперболой с асимптотами x = 2, y = 4.

Решение – точка A(1; 3) и треугольник BCD, заданный системой трех неравенств:
\( \left\{ \begin{array}{ l } \mathrm{x \geq 2} & \\ \mathrm{y \leq 8 - x} & \\ \mathrm{y \geq x} & \end{array}\right. \)

б) \( \left\{ \begin{array}{ l } \mathrm{1\leq |x+y|\leq 3} & \\ \mathrm{2\leq |x-y|\leq 5} & \end{array}\right. \)
Первое неравенство: \( \mathrm{1\leq |x+y|\leq 3\Rightarrow -3\leq x+y\leq -1\cup 1\leq x+y\leq 3\Rightarrow} \)
\( \mathrm{\Rightarrow -x-3\leq y\leq -x-1\cup -x+1\leq y\leq -x+3} \) – две полосы, параллельные y = –x.
Второе неравенство: \( \mathrm{2\leq |x-y|\leq 5\Rightarrow -5\leq x-y\leq -2\cup 2\leq x-y\leq 5\Rightarrow} \)
\( \mathrm{\Rightarrow -x-5\leq -y\leq -x-2\cup -x+2\leq -y\leq -x+5\Rightarrow} \)
\( \mathrm{\Rightarrow x+2\leq y\leq x+5\cup x-5\leq y\leq x-2} \) – две полосы, параллельные y = x.

Решение – четыре прямоугольника, образованные пересечением полос.
\( \left\{ \begin{array}{ l } \mathrm{-x-3\leq y\leq -x-1\cup -x+1\leq y \leq -x+3} & \\ \mathrm{x+2\leq y\leq x+5\cup x-5\leq y\leq x -2} & \end{array}\right. \)

Пример 3. Найдите значения параметра a, при которых система имеет ровно два решения:
\( \left\{ \begin{array}{ l } \mathrm{y=x^2-5|x|+4} & \\ \mathrm{y\leq a} & \end{array}\right. \)
y = x² – 5|x| + 4 – парабола y = x² – 5x + 4 = (x – 1)(x – 4), x > 0, отраженная в отрицательную полуплоскость x < 0 относительно оси Y.
Осью симметрии параболы при x > 0 является прямая \( \mathrm{x_0=\frac{x_1+x_2}{2}=\frac{1+4}{2}=2,5} \)
Вершина лежит на оси. Ордината вершины: y₀ = 2,5² – 5 · 2,5 + 4 = –2,25.
В полуплоскости x < 0 вершина расположена симметрично относительно оси Y и имеет ту же ординату.
Значит, при a = –2,25 система имеет два решения:

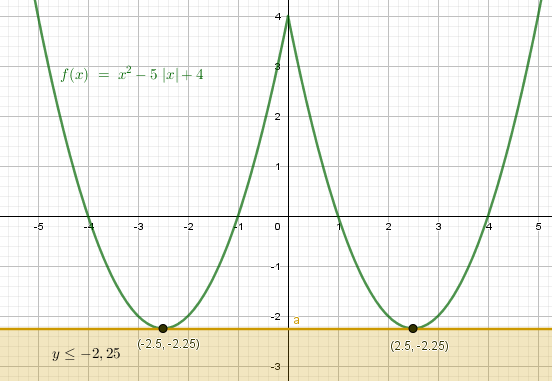
При a < –2,25 решений нет, при a > –2,25 решений бесконечное множество (отрезки кривой).
Ответ: a = –2,25.