Понятие о задачах линейного программирования. Графический метод поиска оптимального решения
п.1. Решение иррациональных систем уравнений
Функция, оптимум которой исследуется, называется целевой функцией.
Ограничения, связанные с конечным количеством ресурсов, называют ресурсными ограничениями. Кроме них, в задаче могут быть и другие ограничения.
Например:
1. Целевая функция – доход предприятия, для которого нужно найти максимум. Ограничения – ресурсы предприятия (сырьё, оборудования, труд), запас которых конечен.
2. Целевая функция – длина маршрута перевозки грузов, для которой нужно искать минимум. Ограничения – фактическая длина пути от каждого поставщика к потребителю, фактические предложения поставщиков и запросы потребителей.
3. Целевая функция – расходы на питание, для которых нужно искать минимум. Ограничения – необходимая калорийность, сбалансированность, состав по клетчатке, витаминам и минералам.
п.2. Задача о максимальном доходе
Рассмотрим классическую задачу о получении максимального дохода от продаж.
Пусть предприятие производит два вида продукции, А и Б, по цене 10 и 15 руб. за единицу. При этом затрачивается три вида ресурсов: сырьё, оборудование и труд. Затраты каждого из ресурсов (в руб.) на производство единицы продукции представлены в таблице. Там же указан общий запас каждого ресурса (в пересчёте на руб.), т.е. ограничение его расхода сверху.
| Ресурс | Затраты на производство единицы продукции, руб. | Запас, руб. | |
| A | Б | ||
| Сырье | 2 | 5 | 400 |
| Оборудование | 1 | 3 | 210 |
| Труд | 1 | 1 | 100 |
Задача: разработать такой план производства по каждому из видов продукции, чтобы получить максимальный доход от продаж.
Пусть x – количество изделий А, y - количество изделий Б, по нашему плану.
Целевая функция: доход от продаж f(x, y) = 10x + 15y → max
Ресурсные ограничения: \begin{gather*} \left\{ \begin{array}{ l } \mathrm{3x+5y\leq 400} & \\ \mathrm{x+3y\leq 210} & \\ \mathrm{x+y=100} & \end{array}\right.\\ \mathrm{x\geq 0,\ \ y\geq 0} \end{gather*} Последние два неравенства – о том, что количество изделий не может быть отрицательным, и на графике мы работаем только в первой четверти координатной плоскости.
Отмечаем на координатной плоскости все ограничения. Полученное множество – пятиугольник ABCDE - множество допустимых решений нашей задачи.
Коэффициенты целевой функции задают вектор \( \mathrm{\overrightarrow{a}=(10;\ 15).} \)
Все прямые доходов от продаж 10x + 15y = F, где F - какое-то число, будут перпендикулярны вектору \( \mathrm{\overrightarrow{a}.} \)
Наша задача – построить прямую через точку 10$x_0$ + 15$y_0$ = $F_{max}$, перпендикулярную вектору \( \mathrm{\overrightarrow{a}} \), как можно выше, но так чтобы точка ($x_0$, $y_0$) всё ещё входила в множество допустимых решений.
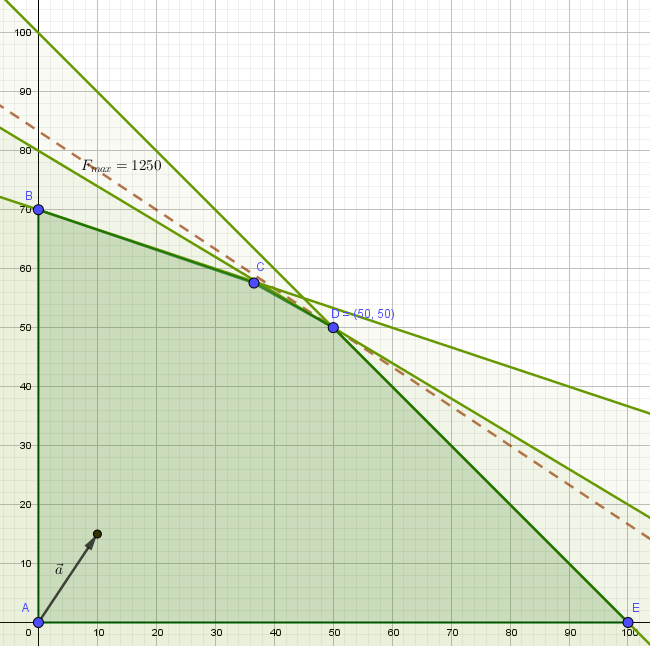
В нашем случае такой точкой является вершина D(50; 50).
Прямая 10x + 15y = 10 · 50 + 15 · 50 = 1250 соответствует решению – максимально возможному доходу.
План производства: x = 50 изделий А, y = 50 изделий Б.
Максимальный доход от продаж: 1250 руб.
п.3. Задача о рациональном питании
Рассмотрим задачу о составлении оптимального рациона питания на неделю.
Пусть наибольшие расходы семейного бюджета идут на мясо и фрукты, в среднем по 600 и 150 рублей за килограмм. Нормы питания на неделю и количество питательных веществ при перерасчёте на кг даны в таблице.
| Питательные вещества | Количество питательных веществ на 1 кг | Норма на неделю | |
| Мясо | Фрукты | ||
| Белки, г | 300 | 50 | 700 |
| Животные жиры, г | 200 | 0 | 700 |
| Витамины, мг | 50 | 150 | 600 |
| Клетчатка, г | 50 | 250 | 1000 |
Задача: необходимо свести расходы к минимуму, но при этом обеспечить нужное количество (не ниже нормы) белков, животных жиров, витаминов и клетчатки.
Пусть x – количество мяса, кг, y - количество фруктов, кг, по нашему плану.
Целевая функция: расходы на покупку f(x, y) = 600x + 150y → min
Ограничения по нормам: \begin{gather*} \left\{ \begin{array}{ l } \mathrm{300x+50y\geq 700} & \\ \mathrm{200x\geq 700} & \\ \mathrm{50x+150y\geq 600} & \\ \mathrm{50x+250y\geq 1000} & \end{array}\right.\\ \mathrm{x\geq 0,\ \ y\geq 0} \end{gather*} Отмечаем на координатной плоскости все ограничения. Полученное множество допустимых решений – часть первой четверти координатной плоскости, ограниченная слева лучом AB и снизу – отрезком AC.
Коэффициенты целевой функции задают вектор \( \mathrm{\overrightarrow{a}=(600;\ 150).} \)
Мы можем его сократить для удобства, т.к. при построении нас интересует направление, а не длина вектора. Пусть \( \mathrm{\overrightarrow{b}=(4;\ 1)} \) ↑↑ \( \mathrm{\overrightarrow{a}.} \)
Все прямые расходов 600x + 150y = F будут перпендикулярны вектору \( \mathrm{\overrightarrow{b}.} \)
Наша задача – построить прямую через точку 600$x_0$ + 150$y_0$ = $F_{min}$, перпендикулярную вектору \( \mathrm{\overrightarrow{b},} \) как можно ниже, но так чтобы точка ($x_0$, $y_0$) всё ещё входила в множество допустимых решений.
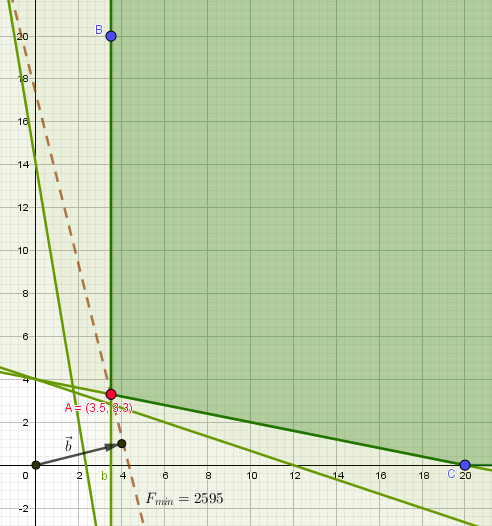
В нашем случае такой точкой является вершина A(3,5; 3,3).
Прямая 600x + 150y = 600 · 3,5 + 150 · 3,3 = 2595 соответствует решению – минимально возможным расходам.
План закупок на неделю: x = 3,5 кг мяса, y = 3,3 кг фруктов.
Минимальная стоимость закупок: 2595 руб.


