Иррациональные неравенства

п.1. Алгоритмы решения иррациональных неравенств с нечётными корнями

Если n – нечётное число, a - некоторое действительное число, f(x) - некоторая функция от переменной x, то:

Например:

Решим неравенство: \(\mathrm{\sqrt[5]{x^2-12x}\gt -2}\)
Возводим в 5-ю степень обе части неравенства: $$ \mathrm{x^2-12x\gt(-2)^5\Rightarrow x^2-12x+32\gt 0\Rightarrow(x-8)(x-4)\gt 0\Rightarrow x\lt 4\cup x\gt 8} $$ Ответ: \(\mathrm{x\in(-\infty;4)\cup(8;+\infty)}\).

Если n – нечётное число, f(x), g(x) - некоторые функции от переменной x, то:

Например:

Решим неравенство: \(\mathrm{\sqrt[3]{7-x^3}\gt 1-x}\)
Возводим в куб обе части неравенства: \begin{gather*} \mathrm{7-x^3\gt (1-x)^3\Rightarrow 7-x^3\gt 1-3x+3x^2-x^3\Rightarrow 3x^2-3x-6\lt 0\Rightarrow }\\ \mathrm{x^2-x-2\lt 0\Rightarrow(x+1)(x-2)\lt 0\Rightarrow -1\lt x\lt 2} \end{gather*} Ответ: \(\mathrm{x\in(-1;2)}\).

п.2. Алгоритмы решения иррациональных неравенств с чётными корнями

Если n – чётное число, a - некоторое действительное число, f(x) - некоторая функция от переменной x, то:

Например: Решим неравенство \(\mathrm{\sqrt{x^2+3x}\lt 2}\)
Решаем систему:
$ \left\{ \begin{array}{ l l } \mathrm{x^2+3x \geq 8} & \\ \mathrm{x^2+3x\lt 2^2} & \end{array}\right. \Rightarrow \left[ \begin{array}{ l l } \mathrm{x(x+3)\geq 0} & \\ \mathrm{x^2+3x-4\lt 0} & \end{array}\right. \Rightarrow \left\{ \begin{array}{ l l } \mathrm{x(x+3)}\geq 0 & \\ \mathrm{(x+4)(x-1)\lt 0} & \end{array}\right. $

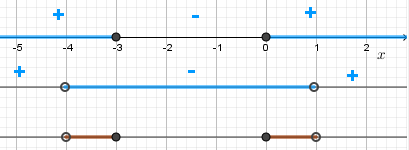
Ответ: \(\mathrm{x\in(-4;-3]\cup[0;1)}\)

Если n – чётное число, f(x), g(x) - некоторые функции от переменной x, то:

Например:

Решим неравенство: \(\mathrm{4\sqrt{5-x}\gt 8-x}\)
\begin{gather*} \mathrm{\sqrt{5-x}\gt\frac{8-x}{4}}\Rightarrow \left[ \begin{array}{ l l } \left\{\begin{array}{ l l} \mathrm{\frac{8-x}{4}\lt 0} & \\ \mathrm{5-x\geq 0} \end{array}\right. & \\ \left\{\begin{array}{ l l } \mathrm{\frac{8-x}{4}\geq 0} & \\ \mathrm{5-x\gt\left(\frac{8-x}{4}\right)^2} & \end{array}\right. \end{array}\right.\Rightarrow \left[ \begin{array}{ l l } \left\{\begin{array}{ l l} \mathrm{8-x\lt 0} & \\ \mathrm{x\geq 5} \end{array}\right. & \\ \left\{\begin{array}{ l l } \mathrm{8-x\geq 0} & \\ \mathrm{16(5-x)\gt 64-16x+x^2} & \end{array}\right. \end{array}\right.\Rightarrow \\ \Rightarrow \left[ \begin{array}{ l l } \left\{\begin{array}{ l l} \mathrm{x\gt 8} & \\ \mathrm{x\leq 5} \end{array}\right. & \\ \left\{\begin{array}{ l l } \mathrm{x\leq 8} & \\ \mathrm{x^2-16\lt 0} & \end{array}\right. \end{array}\right.\Rightarrow \left[ \begin{array}{ l l } \varnothing & \\ \left\{\begin{array}{ l l } \mathrm{x\leq 8} & \\ \mathrm{(x+4)(x-4)\lt 0} & \end{array}\right. \end{array}\right.\Rightarrow \left\{\begin{array}{ l l } \mathrm{x\leq 8} & \\ \mathrm{-4\lt x \lt 4} & \end{array}\right.\Rightarrow -4\lt x\lt 4 \end{gather*} Ответ: \(\mathrm{x\in(-4;4)}\).

п.3. Примеры

Пример 1. Решите неравенства:
а) \(\mathrm{\sqrt[3]{x+2}\gt 3}\)
Возводим в куб обе части неравенства:
$$ \mathrm{x+2\gt 3^3\Rightarrow x\gt 25} $$ Ответ: \(\mathrm{x\in(25;+\infty)}\).

б) \(\mathrm{\sqrt[5]{x^2-8}\leq \sqrt[5]{2x}}\)
Возводим в 5-ю степень обе части неравенства:
$$ \mathrm{ x^2-8\leq 2x\Rightarrow x^2-2x-8\leq 0\Rightarrow (x+2)(x-4)\leq 0\Rightarrow -2\leq x\leq 4 } $$ Ответ: \(\mathrm{x\in\left[-2;4\right]}\)

в) \(\mathrm{\sqrt{x+2}\lt 3}\)
Решаем систему: \begin{gather*} \left\{ \begin{array}{ l l } \mathrm{x+2\geq 0} & \\ \mathrm{x+2\lt 3^2} & \end{array}\right.\Rightarrow \left\{ \begin{array}{ l l } \mathrm{x\geq -2} & \\ \mathrm{x\lt 7} & \end{array}\right.\Rightarrow -2\geq x\lt 7 \end{gather*} Ответ: \(\mathrm{x\in\left[-2;7\right]}\).

г) \(\mathrm{\sqrt{x-5}\lt 7-x}\)
Решаем систему: \begin{gather*} \left\{ \begin{array}{ l l l } \mathrm{x-5\geq 0} & \\ \mathrm{7-x\gt 0} & \\ \mathrm{x-5\lt (7-x)^2} & \end{array}\right.\Rightarrow \left\{ \begin{array}{ l l l } \mathrm{x\geq 5} & \\ \mathrm{x\gt 7} & \\ \mathrm{x-5\lt 49-14x+x^2} & \end{array}\right.\Rightarrow \left\{ \begin{array}{ l l } \mathrm{5\leq x\lt 7} & \\ \mathrm{x^2-15x+54\gt 0} & \end{array}\right.\Rightarrow \\ \Rightarrow \left\{ \begin{array}{ l l } \mathrm{5\leq x\lt 7} & \\ \mathrm{(x-6)(x-9)\gt 0} & \end{array}\right. \end{gather*}

Ответ: \(\mathrm{x\in[5;6)}\).

Пример 2*. Решите неравенства:
а) \(\mathrm{\sqrt{2x+2\sqrt{x^2-9}}\gt\sqrt{x-3}}\)
Возводим в квадрат обе части, записываем ОДЗ: \begin{gather*} \left\{ \begin{array}{ l l l} \mathrm{2x+2\sqrt{x^2-9}\geq 0} & \\ \mathrm{x-3\geq 0} & \\ \mathrm{2x+2\sqrt{x^2-9}\gt x-3} & \end{array}\right.\Rightarrow \left\{ \begin{array}{ l l l} \mathrm{\sqrt{x^2-9}\geq -x} & \\ \mathrm{x\geq 3} & \\ \mathrm{\sqrt{x^2-9}\gt \frac{-x-3}{2}} & \end{array}\right. \end{gather*} Требование x ≥ 3 упрощает решение, т.к. тогда -x ≤ -3 < 0 – отрицательное \(\mathrm{\frac{-x-3}{2}\leq 0}\) – также отрицательное. Получаем, что в первом и третьем неравенстве достаточно найти ОДЗ: \begin{gather*} \left\{ \begin{array}{ l l } \mathrm{x\geq 3} & \\ \mathrm{x^2 -9\geq 0} & \end{array}\right.\Rightarrow \left\{ \begin{array}{ l l } \mathrm{x\geq 3} & \\ \mathrm{(x+3)(x-3)\geq 0} & \end{array}\right.\Rightarrow \left\{ \begin{array}{ l l } \mathrm{x\geq 3} & \\ \mathrm{x\leq -3 \cup x\geq 3} & \end{array}\right.\Rightarrow \mathrm{x\geq 3} \end{gather*}

Ответ: \(\mathrm{x\in[3;+\infty)}\).

б) \(\mathrm{(x^2-25)\sqrt{49-x^2}}>0\)
Решаем систему: \begin{gather*} \left\{ \begin{array}{ l l } \mathrm{49-x^2\gt 0} & \\ \mathrm{x^2-25\gt 0} & \end{array}\right.\Rightarrow \left\{ \begin{array}{ l l } \mathrm{x^2-49\lt 0} & \\ \mathrm{x^2-25\gt 0} & \end{array}\right.\Rightarrow \left\{ \begin{array}{ l l } \mathrm{-7\lt x\lt 7} & \\ \mathrm{x\lt -5\cup x\gt 5} & \end{array}\right.\Rightarrow \\ \Rightarrow \mathrm{-7\lt x\lt -5\cup 5\lt x\lt 7} \end{gather*}

Ответ: \(\mathrm{x\in(-7;-5)\cup(5;7)}\).

в) \(\mathrm{\frac{\sqrt{x+7}-1}{6-\sqrt{x+7}}\geq 0}\)
Замена переменных: \begin{gather*} \left\{ \begin{array}{ l l } \mathrm{z=\sqrt{x+7}\geq 0} & \\ \mathrm{\frac{z-1}{6-z}\geq 0} & \end{array}\right. \end{gather*} Решаем систему: \begin{gather*} \left\{ \begin{array}{ l l } \mathrm{z\geq 0} & \\ \mathrm{\frac{z-1}{z-6}\leq 0} & \end{array}\right. \end{gather*}

$$ \mathrm{ 1\leq z\lt 6 \Rightarrow 1\leq \sqrt{x+7}\lt 6\Rightarrow 1\leq x+7\lt 36\Rightarrow -6\leq x\lt 19 } $$

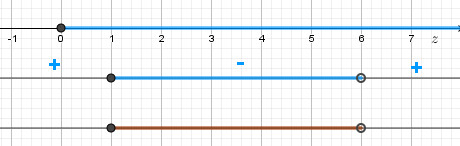
Ответ: \(\mathrm{x\in[-6;19)}\).

г) \(\mathrm{2-\sqrt{1-x}\lt\sqrt[3]{x+3}}\)
Замена переменных: \begin{gather*} \left\{ \begin{array}{ l l } \mathrm{z=x+3} & \\ \mathrm{2-\sqrt{4-z}\lt\sqrt[3]{z}} & \end{array}\right. \end{gather*} Возводим в куб обе части неравенства: \begin{gather*} \mathrm{\left(2-\sqrt{4-z}\right)^3\lt z} \\ \mathrm{8-3\cdot 4\sqrt{4-z}+3\cdot 2(4-z)-(4-z)\sqrt{4-z}\lt z}\\ \mathrm{32-6z+(z-16)\sqrt{4-z}\lt z}\\ \mathrm{(z-16)\sqrt{4-z}\lt 7z-32} \end{gather*} Требование ОДЗ z ≤ 4 означает, что скобка (z - 16) ≤ -12 < 0 - отрицательная, т.е., если на неё разделить левую и правую части, знак неравенства поменяется. \begin{gather*} \sqrt{4-z}\gt\frac{7z-32}{z-16}\Rightarrow \left[ \begin{array}{ l l } \left\{\begin{array}{ l l} \mathrm{\frac{7z-32}{z-16}\lt 0} & \\ \mathrm{z\leq 4} \end{array}\right. & \\ \left\{\begin{array}{ l l } \mathrm{\frac{7z-32}{z-16}\gt 0} & \\ \mathrm{4-z\gt\left(\frac{7z-32}{z-16}\right)^2} & \end{array}\right. \end{array}\right.\Rightarrow \left[ \begin{array}{ l l } \left\{\begin{array}{ l l} \mathrm{\frac{32}{7}\lt z\lt 16} & \\ \mathrm{z\leq 4} \end{array}\right. & \\ \left\{\begin{array}{ l l } \mathrm{z\lt\frac{32}{7}\cup z\gt 16} & \\ \mathrm{(4-z)(z-16)^2\gt (7z-32)^2} & \end{array}\right. \end{array}\right. \end{gather*} Получаем: \begin{gather*} \left\{ \begin{array}{ l l } \mathrm{z\leq 4} & \\ \mathrm{(4-z)(z^2-32z+256)\gt 49z^2-448z+1024} & \end{array}\right. \end{gather*} Решаем нижнее неравенство: \begin{gather*} \mathrm{4z^2-128z+1024-z^3+32z^2-256z\gt 49z^2-448z+1024} \\ \mathrm{-z^3-13z^2+64z\gt 0\Rightarrow z^3+13z^2-64z\gt 0\Rightarrow z(z^2+13z-64)\gt 0}\\ \mathrm{D=13^2-4\cdot(-64)=425,\ \ z_{1,2}=\frac{-13\pm 5\sqrt{17}}{2}} \end{gather*} Возвращаемся к исходной переменной: x = z – 3. Получаем систему: \begin{gather*} \left\{ \begin{array}{ l l } \mathrm{x\leq 1} & \\ \mathrm{(x+3)(x-x_1)(x-x_2)\lt 0} & \end{array}\right.\ \ \mathrm{x_{1,2}=\frac{-19\pm 5\sqrt{17}}{2}} \end{gather*}

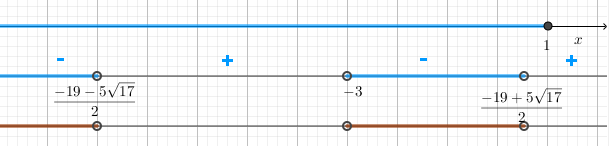
Ответ: \(\mathrm{x\in\left(-\infty;\frac{-19- 5\sqrt{17}}{2}\right)\cup \left(-3;\frac{-19+ 5\sqrt{17}}{2}\right)}\).