Графики арифметических корней n-й степени $y = \sqrt[n]{x}$
Графики функций $y = \sqrt{x}, y = \sqrt[3]{x}, y = \sqrt[4]{x}, y = \sqrt[5]{x}$
С графиком $y = \sqrt{x}$ – «половиной» параболы - мы уже встречались
(см. §22 справочника для 8 класса).
Построим по точкам графики $y = \sqrt[3]{x}, y = \sqrt[4]{x}, y = \sqrt[5]{x}$ и изобразим все графики в одной системе координат.
![Графики функций $y = \sqrt{x}, y = \sqrt[3]{x}, y = \sqrt[4]{x}, y = \sqrt[5]{x}$](/sprav-img/algebra-9-klass/algebra-p-4-1.png)
Заметим, что при $0 \lt x \lt 1$ выполняется неравенсто $\sqrt{x} \lt \sqrt[3]{x} \lt \sqrt[4]{x} \lt \sqrt[5]{x}$
А при $x \gt 1$ выполняется неравенство $\sqrt[5]{x} \lt \sqrt[4]{x} \lt \sqrt[3]{x} \lt \sqrt{x}$
Графики корня n-й степени $y = \sqrt[n]{x}$
|
Корень $y = \sqrt[n]{x}$ с натуральным чётным показателем n возрастает на всей области определения Область определения $x \ge 0,т.е.x \in [0;+ \infty)$ Область значений $y \ge 0,т.е.y \in [0;+ \infty)$ |
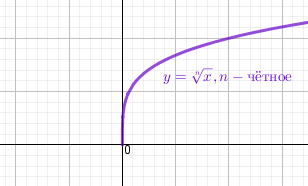 |
|
Корень $y = \sqrt[n]{x}$ с натуральным нечётным показателем n возрастает на всей области определения Область определения $x \in \Bbb R, т.е. x \in (- \infty;+ \infty)$ Область значений $y \in \Bbb R, т.е. y \in (- \infty;+ \infty)$ График симметричен относительно начала координат. Функция нечётная y(-x) = -y(x) |
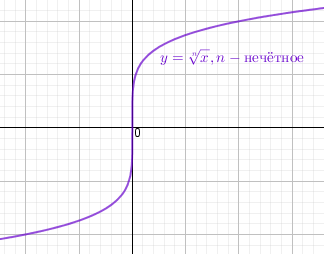 |
Т.к. функция возрастает, можно утверждать, что для неотрицательных $a \ge 0$ и $b \ge 0$ и любом натуральном $n \ge 2$:
$$ a \gt b \iff \sqrt[n]{a} \gt \sqrt[n]{b}, a = b \iff \sqrt[n]{a} = \sqrt[n]{b}, a \lt b \iff \sqrt[n]{a} \lt \sqrt[n]{b} $$
Знак сравнения между аргументами сохраняется для функции.
Если n – нечётное, знак сравнения сохраняется для любых действительных $a, b \in \Bbb R$.
Внимание!
В неравенствах возводить одновременно в чётную степень обе стороны можно только при условии, что обе стороны неотрицательны.
При выполнении этого условия знак неравенства сохраняется.
Иначе – знак неравенства не сохраняется, и получаем ложное высказывание.
Возводить одновременно в нечётную степень можно в любом случае.
Например:
Для чётной степени:
$4 \gt 3 \Rightarrow 4^2 \gt 3^2$, т.е. $16 \gt 9$ - знак сохраняется, высказывание истинное
$2 \gt -3 \require{enclose} \enclose{updiagonalstrike}{\Rightarrow} 2^2 \gt (-3)^2$, т.к. $4 \gt 9$ - ложное высказывание
$-3 \gt -5 \require{enclose} \enclose{updiagonalstrike}{\Rightarrow} (-3)^2 \gt (-5)^2$, т.к. $9 \gt 25$ - ложное высказывание
Для нечётной степени:
$4 \gt 3 \Rightarrow 4^3 \gt 3^3$, т.е. $64 \gt 27$ – истина
$2 \gt -3 \Rightarrow 2^3 \gt (-3)^3$, т.е. $8 \gt -27$ – истина
$-3 \gt -5 \Rightarrow (-3)^3 \gt (-5)^3$, т.е. $-27 \gt -125$ – истина
Корень n-й степени $y = \sqrt[n]{x}$ и степенная функция $y = x^n$ как взаимно обратные функции
Найдём функцию, обратную $y = \sqrt[n]{x}$ (см. §2 данного справочника)
Меняем обозначения аргумента и результата: $x = \sqrt[n]{y} \Rightarrow x^n = (\sqrt[n]{y})^n \Rightarrow y = x^n$ – искомая обратная функция.
При чётном n необходимо учесть ограничения на $x:x \ge 0$ и $y:y \ge 0$.
|
Для корня $y = \sqrt[n]{x}$ с натуральным чётным показателем n обратной функцией является $y = x^n$ с ограничениями: $x \ge 0,т.е.x \in [0;+ \infty)$ $y \ge 0,т.е.y \in [0;+ \infty)$ |
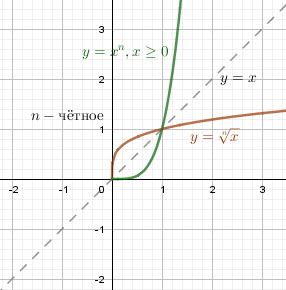 |
|
Для корня $y = \sqrt[n]{x}$ с натуральным нечётным показателем n обратной функцией является $y = x^n$ без ограничений: $x \in \Bbb R, т.е. x \in (- \infty;+ \infty)$ $y \in \Bbb R, т.е. y \in (- \infty;+ \infty)$ |
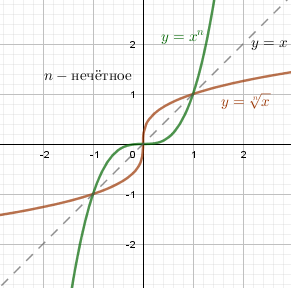 |
Примеры
Пример 1. Решите уравнение:
$а) \sqrt[3]{50-x^2} = 1$
$( \sqrt[3]{50-x^2})^3 = 1^3 $
$50-x^2 = 1 $
$49-x^2 = 0 $
(7-x)(7+x) = 0
$x = \pm 7$
$ б) \sqrt[4]{x^2+12} = 2$
$ (\sqrt[4]{x^2+12})^4 = 2^4 $
$ x^2+12 = 16 $
$x^2-4 = 0$
(x-2)(x+2) = 0
$x = \pm 2$
$ в) \sqrt[5]{x^2-33} = -2 $
$ (\sqrt[5]{x^2-33})^5 = (-2)^5 $
$ x^2-33 = -32 $
$ x^2-1 = 0 $
(x-1)(x+1) = 0
$x = \pm 1$
$ г) \sqrt[6]{37-x^2} = -1$
Корень чётной степени не может быть отрицательным.
$x \in \varnothing$ - решений нет
Пример 2. Решите неравенство:
$ а) \sqrt[3]{71-x} \lt 4 $
$ (\sqrt[3]{71-x})^3 \lt 4^3 $
$ 71-x \lt 64 $
$ -x \lt -7 $
$ x \gt 7 $
$ x \in (7;+ \infty) $
$ б) \sqrt[3]{71-x} \lt -4 $
$ (\sqrt[3]{71-x})^3 \lt (-4)^3 $
$ 71-x \lt -64 $
$ -x \lt -135 $
$ x \gt 135 $
$ x \in (135;+ \infty) $
$ в) \sqrt[4]{12+x} \gt 2 $
$ ( \sqrt[4]{12+x})^4 \gt 2^4 $
$ 12+x \gt 16 $
$ x \gt 4 $
$ x \in (4;+ \infty) $
$ г)\sqrt[4]{12+x} \gt -2 $
Корень чётной степени всегда неотрицательный. Решение сводится к поиску ОДЗ:
$ 12+x \ge 0 $
$ x \ge -12 $
$ x \in [-12;+\infty) $
Пример 3. Решите графически уравнение $\sqrt[3]{x} = 2-x$
При каких x выполняется неравенство $\sqrt[3]{x} \gt 2-x, \sqrt[3]{x} \lt 2-x$?
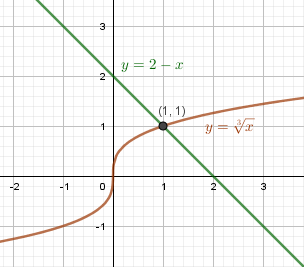
Корень уравнения: x = 1
$\sqrt[3]{x} \gt 2-x$ при $x \gt 1$ (кривая расположена над прямой)
$\sqrt[3]{x} \lt 2-x$ при $x \lt 1$ (кривая расположена под прямой)
Пример 4. Решите графически уравнение $\sqrt[4]{x} = x$
При каких x выполняется неравенство $\sqrt[4]{x} \gt x, \sqrt[4]{x} \lt x$?
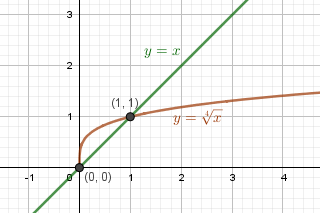
Корни уравнения: $x_1 = 0, x_2 = 1$
$\sqrt[4]{x} \gt x$ при $0 \lt x \lt 1$ (кривая расположена над прямой)
$\sqrt[4]{x} \lt x$ при $x \gt 1$ (кривая расположена под прямой)
Пример 5*. Постройте в одной системе координат графики функций:
$$ y = \sqrt[3]{x}, y = \sqrt[6]{x^2-2x+1}, y = -|x-1|^{\frac{1}{3}} $$
Сделайте выводы.
Преобразуем уравнения функций:
$$ y = \sqrt[6]{x^2-2x+1} = \sqrt[6]{(x-1)^2} = |x-1|^{\frac{1}{3}} = \left[ \begin{array}{cc} (x-1)^{\frac{1}{3}},x \ge 1 \\ (1-x)^{\frac{1}{3}}, x \lt 1 \end{array} \right. $$
$$ y = -|x-1|^{\frac{1}{3}} = \left[ \begin{array}{cc} -(x-1)^{\frac{1}{3}}, x \ge 1 \\ -(1-x)^{\frac{1}{3}}, x \lt 1 \end{array} \right. $$
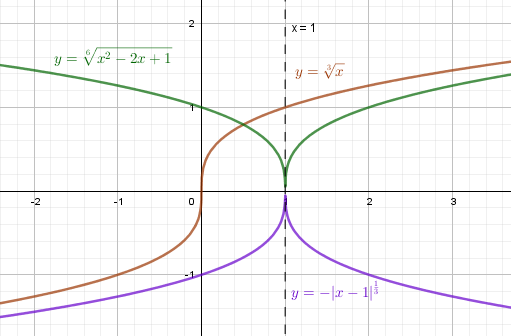
График $y = \sqrt[6]{x^2-2x+1} = |x-1|^{\frac{1}{3}}$ симметричен относительно вертикальной оси x = 1. Ветка параболы $(x-1)^{\frac{1}{3}}$ получается сдвигом положительной ветки параболы $y = \sqrt[3]{x}$ на 1 вправо. Ветка параболы $(1-x)^{\frac{1}{3}}$ получается зеркальным отражением ветки $(x-1)^{\frac{1}{3}}$ относительно вертикальной оси x = 1.
График $y = -|x-1|^{\frac{1}{3}}$ является отражением графика $y = \sqrt[6]{x^2-2x+1}$ относительно оси абсцисс OX.


