Геометрическая вероятность

Понятие геометрической вероятности было сформулировано в §37 данного справочника. В этом параграфе мы рассмотрим различные задачи, при решении которых используется геометрическая вероятность.

п.1. Геометрическая вероятность на прямой

В одномерном случае пространству всех событий соответствует длина отрезка Ω ↔ L. Событие A ↔ l_A – попадание в отрезок l_A ≤ L.
Тогда вероятность события A $$ \mathrm{ P(A)=\frac{l_A}{L} } $$ Говорят, что мерой множеств событий в одномерном случае является длина.

Например:
Оптический кабель длиной 1 м случайно разрезают ножницами. Какова вероятность того, что длина обрезка составляет не меньше 80 см?

Чтобы получить обрезок не менее 80 см, нужно попасть ножницами в отрезок 20 см справа или слева куска кабеля. Вероятности попадания \(\mathrm{P_{\text{справа}}=\frac{l_A}{L},\ P_{\text{слева}}=\frac{l_A}{L}}\). По правилу суммы, искомая вероятность при L=100 см, l_A=20 см $$ \mathrm{ P_{\text{справа}}+P_{\text{слева}}=\frac{2l_A}{L},\ \ P=\frac{2\cdot 20}{100}=0,4 } $$ Ответ: 0,4.

п.2. Геометрическая вероятность на плоскости

В двумерном случае пространству всех событий соответствует площадь некоторой замкнутой области Ω ↔ S_Ω.
Событие A ↔ s_A – попадание в замкнутую подобласть с площадью s_A ≤ S_Ω.
Тогда вероятность события A $$ \mathrm{ P(A)=\frac{s_A}{S_{\Omega}} } $$ Говорят, что мерой множеств событий в двумерном случае является площадь.

Например:
Два друга договорились встретиться между 14 и 15 часами. Каждый может прийти в любой момент в течение назначенного часа. Тот, кто пришёл первым, ждёт другого в течение 15 минут, а затем уходит. Чему равна вероятность встречи?

Пусть 0≤x≤60 (мин) и 0≤y≤60 (мин) – моменты прихода первого и второго друга соответственно. Тогда пространство событий – квадрат 60х60.
Область ожидания: |x–y|≤15. Раскроем модуль: –15≤x–y≤15. Получаем систему: \(\left\{ \begin{array}{ l} \mathrm{y\leq x+15} &\\ \mathrm{y\geq x-15} & \end{array}\right. \). На графике – это зелёная полоса. Событие A – встреча состоялась – соответствует площади зеленой полосы. Получаем: \begin{gather*} \mathrm{ S_{\Omega}=60\cdot 60=3600,\ \ s_A=3600-2S_{\Delta}=3600-2\cdot \frac{1}{2}\cdot 45^2=1575 }\\ \mathrm{ P(A)=\frac{s_A}{S_{\Omega}}=\frac{1575}{3600}=\frac{7}{16}=0,4375 } \end{gather*} Ответ: 0,4375.

п.3. Геометрическая вероятность в пространстве

В трёхмерном случае пространству всех событий соответствует объём некоторой замкнутой области Ω ↔ V_Ω.
Событие A ↔ v_A – попадание в замкнутую подобласть с объёмом v_A ≤ V_Ω.
Тогда вероятность события A $$ \mathrm{ P(A)=\frac{v_A}{V_{\Omega}} } $$ Говорят, что мерой множеств событий в трёхмерном случае является объём.

Например:
Телескоп находится на космической станции. В каждый момент времени он случайно направлен в одну из сторон и наблюдает часть неба. Пусть телескоп способен регистрировать все объекты в радиусе 10000 км. Какова вероятность, что он заметит астероид радиусом 100 км, залетевший в область регистрации?

Пространству всех событий соответствует сфера объемом: $$ \mathrm{ V_{\Omega}=\frac{4}{3}\pi R^3,\ R=10000\ \text{км} } $$ Событие A – астероид замечен – соответствует объему астероида: $$ \mathrm{ v_{A}=\frac{4}{3}\pi R^3,\ R=100\ \text{км} } $$ Вероятность того, что астероид будет замечен: $$ \mathrm{ P(A)=\frac{v_{A}}{V_{\Omega}}=\frac{\frac{4}{3}\pi R^3}{\frac{4}{3}\pi R^3}=\left(\frac{r}{R}\right)^3,\ \ P(A)=\left(\frac{100}{10000}\right)^3=10^{-6}=0,000001 } $$ Ответ: 0,000001.

п.4. Примеры

Пример 1. Для игры в «Дартс» используется круглая мишень радиусом 40 см. Центральный круг – «десятка» – имеет радиус 4 см. Если игрок всегда попадает в мишень в любую точку с одинаковой вероятностью, какова вероятность попасть в «десятку»?

Мерой для этой задачи является площадь.
Пространство всех событий – круг радиусом R = 40 см. Его площадь \(\mathrm{ S_{\Omega;}=\pi R^2}\).
Событие A – попадание в «десятку» – круг радиусом r = 4 см. Его площадь \(\mathrm{ s_{A}=\pi r^2}\).
Вероятность попадания: $$ \mathrm{ P(A)=\frac{s_{A}}{S_{\Omega}}=\frac{\pi r^2}{\pi R^2}=\left(\frac{r}{R}\right)^2,\ \ P(A)=\left(\frac{4}{40}\right)^2=0,01 } $$ Ответ: 0,01.

Пример 2. В правильный треугольник вписан полукруг. В треугольник случайно ставятся точки. Какова вероятность, что точка попадет в полукруг?

Мерой в данной задаче является площадь.
Пусть сторона треугольника a. Тогда пространство всех событий – треугольник площадью \(\mathrm{ S_{\Omega}=\frac{\sqrt{3}}{4}a^2}\).
Найдем радиус вписанного полукруга.
ΔCOB ~ ΔOEB – по двум углам. $$ \mathrm{ \frac{CO}{OE}=\frac{CB}{OB}\Rightarrow\frac{a\cdot sin60^{\circ}}{r}=\frac{a}{a/2}\Rightarrow r=\frac{a}{2}\cdot sin60^{\circ}=\frac{\sqrt{3}}{4}a } $$ Площадь вписанного полукруга: \(\mathrm{ s_{A}=\frac{\pi r^2}{2}=\frac{\pi}{2}\left(\frac{\sqrt{3}}{4}a\right)^2=\frac{3\pi}{32}a^2}\).
Вероятность попасть в полукруг: $$ \mathrm{ P(A)=\frac{s_{A}}{S_{\Omega}}=\frac{\frac{3\pi}{32}a^2}{\frac{\sqrt{3}}{4}a^2}=\frac{\sqrt{3}}{8}\pi \approx 0,68 } $$ Ответ: \(\mathrm{ \frac{\sqrt{3}}{8}\pi \approx 0,68. }\)

Пример 3. На отрезке [0; 1] случайным образом выбирается точка. Найдите вероятность того, что её координата x удовлетворяет условиям:
1) x² > 0,64
2) \(\left\{ \begin{array}{ l} \mathrm{0,3x^2\leq 0,027} &\\ \mathrm{2x^2\geq 0,08} & \end{array}\right. \)

1) \(\mathrm{x^2\geq 0,64\Rightarrow (x^2-0,64)\geq 0\Rightarrow (x-0,8)(x+0,8)\geq 0\Rightarrow} \left\{ \begin{array}{ l} \mathrm{x\leq -0,8} &\\ \mathrm{x\geq 0,8} & \end{array}\right. \)
Учитывая x ∈ [0; 1], получаем: $$ \left\{ \begin{array}{ l} \mathrm{0\leq x\leq 1} &\\ \left[ \begin{array}{ l} \mathrm{x\leq -0,8\Rightarrow 0,8\leq x\leq 1} &\\ \mathrm{x\geq 0,8} & \end{array}\right.& \end{array}\right. $$ Мерой в данной задаче является длина: L_Ω = 1, l_A = 1 – 0,8 = 0,2
Вероятность выбора точки при данных условиях: \( \mathrm{P(A)=\frac{0,2}{1}=0,2} \)
\begin{gather*} 2)\ \left\{ \begin{array}{ l} \mathrm{0,3x^2\leq 0,027} &\\ \mathrm{2x^2\geq 0,08} & \end{array}\right. \Rightarrow \left\{ \begin{array}{ l} \mathrm{x^2\leq 0,009} &\\ \mathrm{x^2\geq 0,004} & \end{array}\right. \Rightarrow \left\{ \begin{array}{ l} \mathrm{x^2-0,009\leq 0} &\\ \mathrm{x^2-0,004\geq 0} & \end{array}\right. \Rightarrow \left\{ \begin{array}{ l} \mathrm{(x-0,3)(x+0,3)\leq 0} &\\ \mathrm{(x-0,2)(x+0,2)\geq 0} & \end{array}\right. \Rightarrow \\ \Rightarrow \left\{ \begin{array}{ l} \mathrm{-0,3\leq x\leq 0,3} &\\ \left[ \begin{array}{ l} \mathrm{x\leq -0,2} &\\ \mathrm{x\geq 0,2} & \end{array}\right.& \end{array}\right. \Rightarrow \left[ \begin{array}{ l} \mathrm{-0,3\leq x\leq -0,2} &\\ \mathrm{0,2\leq x\leq 0,3} & \end{array}\right. \end{gather*} Учитывая x ∈ [0; 1], получаем: $$ \left\{ \begin{array}{ l} \mathrm{0\leq x\leq 1} &\\ \left[ \begin{array}{ l} \mathrm{-0,3\leq x\leq -0,2} &\\ \mathrm{0,2\leq x\leq 0,3} & \end{array}\right.& \end{array}\right. \Rightarrow 0,2 \leq x \leq 0,3 $$ Мерой в данной задаче является длина: L_Ω = 1, l_A = 0,3 - 0,2 = 0,1
Вероятность выбора точки при данных условиях: \(\mathrm{P(A)=\frac{0,1}{1}=0,1}\)
Ответ: 1) 0,2; 2) 0,1.

Пример 4. В сито, наполненное до краёв зерном, уронили жемчужину. Сито представляет собой цилиндр радиусом 20 см и высотой 12 см.
1) Какова вероятность случайно зачерпнуть горсть зерна вместе с жемчужиной, если объём горсти 0,1 л?
2) Если после неудачной попытки, высыпать зерно из горсти обратно в сито, перемешать, и снова зачерпнуть горсть, изменится ли вероятность?
3) Если после неудачной попытки, высыпать зерно из горсти в сторону и зачерпнуть следующую горсть, изменится ли вероятность?
4) Сколько «неудачных» горстей нужно отсыпать в сторону, чтобы вероятность удачи для следующей попытки превысила 1/3?
1) Мерой для этой задачи является объём.
Пространство всех событий – все возможные точки, где может оказаться жемчужина – это цилиндрическое сито, объемом

Событие A – зачерпнуть жемчужину в горсти объемом v_A = 0,1 л
Вероятность: $$ \mathrm{ P(A)=\frac{v_{A}}{V_{\Omega}},\ \ P(A)=\frac{0,1}{4,8\pi} \approx 0,0066 } $$ 2) Если высыпать зерно обратно из горсти и перемешать, то пространство всех событий останется тем же, V_Ω = 4,8π л. Вероятность не изменится.

3) Если высыпать зерно в сторону, пространство всех событий уменьшится:

Вероятность увеличится: $$ \mathrm{ P(A)=\frac{v_{A}}{V_{\Omega}^{'}},\ \ P(A)=\frac{0,1}{4,8\pi -0,1} \approx 0,0071 } $$
4) После того, как мы отсыпаем N горстей, пространство всех событий $$ \mathrm{ V_{\Omega}^{''} = V_{\Omega}-Nv_{A}=(4,8\pi-0,1N)\ \text{л} } $$ По условию: $$ \mathrm{ P(A)\frac{0,1}{4,8\pi -0,1N}\geq \frac13 } $$ Получаем: \(\mathrm{4,8\pi -0,1N\lt 0,3\Rightarrow N\gt \frac{4,8\pi-0,3}{0,1}=147,8}\)
N = 148.
Ответ: 1) 0,0066; 2) нет; 3) увеличится, 0,0071; 4) 148.

Пример 5. Загадываются два действительных числа от 0 до 4.
1) Какова вероятность, что их сумма больше 3?
2) Какова вероятность, что их разность меньше 1?

По условию 0 ≤ x ≤ 4, 0 ≤ y ≤ 4
Мерой для этой задачи является площадь.
Пространство всех событий: квадрат 4х4, S_Ω = 4² = 16.

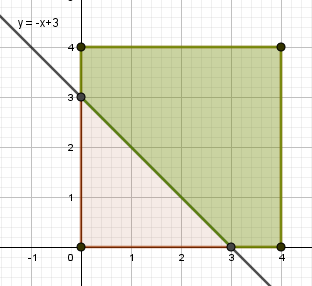	\(\mathrm{x+y\gt 3\Rightarrow}\) \(\mathrm{y\gt -x+3}\) – область над прямой $$ \mathrm{ s_{A}=S_{\Omega}-S_{\Delta}=16-\frac12\cdot 3^2=11,5 } $$ Вероятность для суммы: $$ \mathrm{ P(x+y\gt 3)=\frac{s_{A}}{S_{\Omega}}=\frac{11,5}{16}=\frac{23}{32} } $$
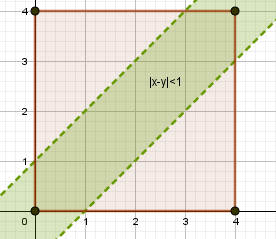	\(\mathrm{|x-y|\lt 1\Rightarrow -1 \lt x-y\lt 1\Rightarrow}\) \( \left\{ \begin{array}{ l} \mathrm{y\geq x+1} &\\ \mathrm{y\leq x-1} & \end{array}\right. \) – полоса $$ \mathrm{ s_{A}=S_{\Omega}-2S_{\Delta}=16-2\cdot\frac12\cdot 3^2=7 } $$ Вероятность для разности: $$ \mathrm{ P(|x-y|\lt 1)=\frac{s_{A}}{S_{\Omega}}=\frac{7}{16} } $$

Ответ: \(\mathrm{ 1) \frac{23}{32};\ \ 2) \frac{7}{16}. }\)