Решение систем неравенств с одной переменной

Понятие системы неравенств с одной переменной и его решения

Например: ${\left\{ \begin{array}{c} x+7 \ge 2 \\ x-4 \lt 1 \end{array} \right.} \iff {\left\{ \begin{array}{c} x \ge -5 \\ x \lt 5 \end{array} \right.} \iff -5 \le x \lt 5 или x \in \Bbb[-5;5)$ - полуинтервал

О пересечении числовых промежутков подробней см. §17 данного справочника

Алгоритм решения системы неравенств с одной переменной

Подробно о числовой прямой и видах числовых промежутков на ней рассказано в §16 данного справочника. Здесь мы изобразим числовые промежутки как решения неравенств на более простых примерах.

Шаг 1. Найти множество частных решений для каждого из неравенств системы. Если хотя бы одно из частных решений является пустым множеством, вся система неравенств не имеет решений; перейти к шагу 4.

Шаг 2. Начертить друг под другом числовые прямые, число которых равно числу полученных частных решений. Начала отсчёта числовых прямых должны находиться на общем перпендикуляре, единичный отрезок должен совпадать .

Шаг 3. На числовых прямых изобразить полученные частные решения, на отдельной прямой найти их пересечение – это и будет общим решением системы .

Шаг 4. Работа завершена.

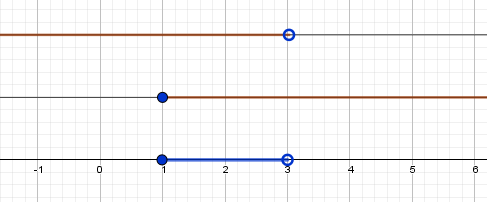
Например: ${\left\{ \begin{array}{c} x-2 \lt 1 \\ x+5 \ge 6 \end{array} \right.} \iff {\left\{ \begin{array}{c} x \lt 3 \\ x \ge 1 \end{array} \right.} \iff 1 \le x \lt 3 или x \in \Bbb[1;3)$ - полуинтервал

Например:

1) В системе $ {\left\{ \begin{array}{c} x \gt 5 \\ x \gt 2 \\ x \gt 3 \end{array} \right.} $ наибольшее число (условие) справа 5.

По принципу «больше большего» останется: $ {\left\{ \begin{array}{c} x \gt 5 \\ x \gt 2 \\ x \gt 3 \end{array} \right.} \iff x \gt 5 $

2) В системе $ {\left\{ \begin{array}{c} x \lt 5 \\ x \lt 2 \\ x \lt 3 \end{array} \right.} $ наименьшее число (условие) справа 2.

По принципу «меньше меньшего» останется: $ {\left\{ \begin{array}{c} x \lt 5 \\ x \lt 2 \\ x \lt 3 \end{array} \right.} \iff x \lt 2 $

Примеры

Пример 1. Решите системы уравнений:

$а) {\left\{ \begin{array}{c} 2(x-8) \ge x-16 \\ 3(x+1) \le 11 \end{array} \right.} \iff {\left\{ \begin{array}{c} 2x-x \ge -16+16 \\ 2x \le 11-3 \end{array} \right.} \iff {\left\{ \begin{array}{c} x \ge 0 \\ 2x \le 8 \end{array} \right.} \iff {\left\{ \begin{array}{c} x \ge 0 \\ x \le 4 \end{array} \right.} \iff 0 \le x \le 4$

$x \in [0;4]$ - интервал

$б) {\left\{ \begin{array}{c} 5(x-6) \gt x-10 \\ 4(x-1) \lt x+5 \end{array} \right.} \iff {\left\{ \begin{array}{c} 5x-x \gt 30-10 \\ 4x-x \lt 5+4 \end{array} \right.} \iff {\left\{ \begin{array}{c} 4x \gt 20 \\ 3x \lt 9 \end{array} \right.} \iff {\left\{ \begin{array}{c} x \gt 5 \\ x \lt 3 \end{array} \right.} \iff x \in \varnothing$

$x \in \varnothing$ - решений нет

$в) {\left\{ \begin{array}{c} -5 \lt 3x+1 \le 4 \\ 3 \lt 2x+5 \lt 9 \end{array} \right.} \iff {\left\{ \begin{array}{c} -5-1 \lt 3x \le 4-1 \\ 3-5 \lt 2x \lt 9-5 \end{array} \right.} \iff {\left\{ \begin{array}{c} -6 \lt 3x \le 3 \\ -2 \lt 2x \lt 4 \end{array} \right.} \iff {\left\{ \begin{array}{c} -2 \lt x \le 1 \\ -1 \lt x \lt 2 \end{array} \right.} \iff$

$$\iff -1 \lt x \le 1$$

$x \in (-1;1] $ - полуинтервал

Пример 2. При каких значениях переменной x имеет смысл выражение:

$ а) \sqrt{x+2} + \sqrt{4-x} $

$ {\left\{ \begin{array}{c} x+2 \ge 0 \\ 4-x \ge 0 \end{array} \right.} \iff {\left\{ \begin{array}{c} x \ge -2 \\ x \le 4 \end{array} \right.} \iff -2 \le x \le 4 $

$x \in [-2;4]$

$ б) \sqrt{2x+3} + \frac{1}{x-4}$

$ {\left\{ \begin{array}{c} 2x+3 \ge 0 \\ x-4 \neq 0 \end{array} \right.} \iff {\left\{ \begin{array}{c} x \ge -1,5 \\ x \neq 4 \end{array} \right.}$

$x \in [-1,5;4) \cup (4;+ \infty) $

$ в) \frac{1}{\sqrt{x-5}} + \frac{1}{\sqrt{1-x}}$

$ {\left\{ \begin{array}{c} x-5 \gt 0 \\ 1-x \gt 0 \end{array} \right.} \iff {\left\{ \begin{array}{c} x \gt 5 \\ x \lt 1 \end{array} \right.} \iff x \in \varnothing$

$x \in \varnothing $ - решений нет

$ г) {\sqrt{x+3}} + \frac{1}{\sqrt{x+1}}$

$ {\left\{ \begin{array}{c} x+3 \ge 0 \\ x+1 \gt 0 \end{array} \right.} \iff {\left\{ \begin{array}{c} x \ge -3 \\ x \gt -1 \end{array} \right.} \iff x>-1$

$x \in (-1;+ \infty) $

Пример 3*. У космического пирата Шутзема несколько затруднительное финансовое положение и только 510 астротугриков в кармане. Однако ему нужно пополнить запасы топлива и продовольствия. Одна капсула с топливом стоит 50 астротугриков, а одна капсула с едой – 30 астротугриков. Какой вариант покупок есть у Шутзема на всю сумму без сдачи, если топлива нужно не менее 4 капсул, а еды – не менее 5?

Пусть x - количество капсул с топливом, y – количество капсул с едой.

По условию задачи:

$$ {\left\{ \begin{array}{c} 50x+30y \le 500 \\ x \ge 4 \\ y \ge 5 \\ x,y \in \Bbb N \end{array} \right.} \iff {\left\{ \begin{array}{c} 5x+3y \le 50 \\ x \ge 4 \\ y \ge 5 \\ x,y \in \Bbb N \end{array} \right.} $$

Изобразим полученные полуплоскости графически и найдём их пересечение.

Прямая сверху – это бюджетное ограничение.

На этой прямой в области допустимых значений (закрашенный треугольник, стороны включительно) есть только одно целое решение: $ {\left\{ \begin{array}{c} x = 6 \\ y = 7 \end{array} \right.} $

Ответ: 6 капсул топлива и 7 капсул еды.