Решение неравенств с одной переменной под знаком модуля

Правило раскрытия модуля в неравенствах

Исходя из сведений о совокупности неравенств (см. §39 данного справочника), для простейшего неравенства с модулем можем записать:

$$ |x| \lt a \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} a \ge 0 \\ |x| \lt a \end{array} \right.} \\ {\left\{ \begin{array}{c} a \lt 0 \\ x \in \varnothing \end{array} \right.} \end{array} \right. \Rightarrow {\left\{ \begin{array}{c} a \ge 0 \\ \left[ \begin{array}{cc} {\left\{ \begin{array}{c} x \lt a \\ x \ge 0 \end{array} \right.} \\ {\left\{ \begin{array}{c} -x \lt a \\ x \lt 0 \end{array} \right.} \end{array} \right. \end{array} \right.} \iff {\left\{ \begin{array}{c} a \ge 0 \\ \left[ \begin{array}{cc} 0 \le x \lt a \\ {\left\{ \begin{array}{c} x \gt -a \\ x \lt 0 \end{array} \right.} \end{array} \right. \end{array} \right.} \iff {\left\{ \begin{array}{c} a \ge 0 \\ \left[ \begin{array}{cc} 0 \le x \lt a \\ -a \lt x \lt 0 \end{array} \right. \end{array} \right.} \iff {\left\{ \begin{array}{c} a \ge 0 \\ -a \lt x \lt a \end{array} \right.} $$

Например:

$ |x| \lt 5 \iff -5 \lt x \lt 5 или x \in (-5;5) $

$ |x| \lt -3 \iff x \in \varnothing$ - решений нет

Рассмотрим неравенство:

$$ |x| \gt a \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} x \gt a \\ x \ge 0 \end{array} \right.} \\ {\left\{ \begin{array}{c} -x \gt a \\ x \lt 0 \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} x \gt a \\ x \ge 0 \end{array} \right.} \\ {\left\{ \begin{array}{c} x \lt -a \\ x \lt 0 \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} a \ge 0 \\ \left[ \begin{array}{cc} x \gt a \\ x \lt -a \end{array} \right. \end{array} \right.} \\ {\left\{ \begin{array}{c} a \lt 0 \\ \left[ \begin{array}{cc} x \ge 0 \\ x \lt 0 \end{array} \right. \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} a \ge 0 \\ x \lt -a \cup x \gt a \end{array} \right.} \\ {\left\{ \begin{array}{c} a \lt 0 \\ x \in \Bbb R \end{array} \right.} \end{array} \right. $$

Например:

$|x| \gt 5 \iff x \lt -5 \cup x \gt 5$ или $x \in (-\infty;-5) \cup (5;+\infty)$

$|x| \gt -3 \iff x \in \Bbb R$ - любое число

Примеры

Пример 1. Решите неравенство:

$а) |x+7| \lt 3$

$|x+7| \lt 3 \iff -3 \lt x+7 \lt 3 \iff -3-7 \lt x \lt 3-7 \iff -10 \lt x \lt -4 $

$ x \in (-10;-4) $

$ б) |x-3| \lt -1 $

Модуль не может быть меньше отрицательного числа:

$x \in \varnothing$, решений нет

$ в) |2x+5| \gt 3 $

$ |2x+5| \gt 3 \iff \left[ \begin{array}{cc} 2x+5 \lt -3 \\ 2x+5 \gt 3 \end{array} \right. \iff \left[ \begin{array}{cc} 2x \lt -8 \\ 2x \gt -2 \end{array} \right. \iff \left[ \begin{array}{cc} x \lt -4 \\ x \gt -1 \end{array} \right. \iff x \lt -4 \cup x \gt -1 $

$x \in (-\infty;-4) \cup (-1;+\infty)$

$ г) |3x+7| \gt -1 $

Модуль всегда больше отрицательного числа:

$x \in \Bbb R$, любое число

Пример 2. Решите двойное неравенство:

$ 1 \lt |5x-4| \lt 11 $

Способ 1

$ 1 \lt |5x-4| \lt 11 \iff {\left\{ \begin{array}{c} |5x-4| \gt 1 \\ |5x-4| \lt 11 \end{array} \right.} \iff {\left\{ \begin{array}{c} \left[ \begin{array}{cc} 5x-4 \lt -1 \\ 5x-4 \gt 1 \end{array} \right. \\ -11 \lt 5x-4 \lt 11 \end{array} \right.} \iff {\left\{ \begin{array}{c} \left[ \begin{array}{cc} 5x \lt 3 \\ 5x \gt 5 \end{array} \right. \\ -7 \lt 5x \lt 15 \end{array} \right.} \iff $

$$ \iff {\left\{ \begin{array}{c} \left[ \begin{array}{cc} x \lt 0,6 \\ x \gt 1 \end{array} \right. \\ -1,4 \lt x \lt 3 \end{array} \right.} \iff {\left\{ \begin{array}{c} x \lt 0,6 \cup x \gt 1 \\ -1,4 \lt x \lt 3 \end{array} \right.} \iff -1,4 \lt x \lt 0,6 \cup 1 \lt x \lt 3 $$

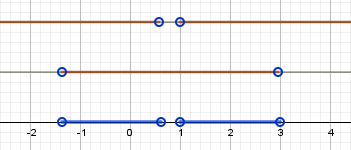
Способ 2

$ 1 \lt |5x-4| \lt 11 \iff \left[ \begin{array}{cc} -11 \lt 5x-4 \lt -1 \\ 1 \lt 5x-4 \lt 11 \end{array} \right. \iff \left[ \begin{array}{cc} -7 \lt 5x \lt 3 \\ 5 \lt 5x \lt 15 \end{array} \right. \iff \left[ \begin{array}{cc} -1,4 \lt x \lt 0,6 \\ 1 \lt x \lt 3 \end{array} \right. $

Ответ: $x \in (-1,4;0,6) \cup (1;3)$

Пример 3. Найдите все целые решения неравенства:

а)$ |x^2+4| \lt 15 $

$$ |x^2+4| \lt 15 \iff -15 \lt x^2+4 \lt 15 \iff -19 \lt x^2 \lt 11 \iff 0 ≤ x^2 \lt 11 $$

Целые решения:

$x \in \{0; \pm 1; \pm 2 \pm 3 \}$

б*) $ |x^2+4x| \lt 5 $

$$ |x^2+4x| \lt 5 \iff -5 \lt x^2+4x \lt 5 \iff {\left\{ \begin{array}{c} x^2+4x \gt -5 \\ x^2+4x \lt 5 \end{array} \right.} \iff {\left\{ \begin{array}{c} x^2+4x+5 \gt 0 \\ x^2+4x-5 \lt 0 \end{array} \right.} $$

В первой параболе $D \lt 0$, координаты вершины (точка минимума):

$x_0 = - \frac{b}{2a} = - \frac{4}{2} = -2, y_0 = 4-8+5 = 1 \gt 0$ - парабола всегда положительна

Первое неравенство выполняется при любом $x \in \Bbb R$.

Решаем второе неравенство:

$$ x^2+4x-5 \lt 0 \iff (x+5)(x-1) \lt 0 \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} x+5 \gt 0 \\ x-1 \lt 0 \end{array} \right.} \\ {\left\{ \begin{array}{c} x+5 \lt 0 \\ x-1 \gt 0 \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} x \gt -5 \\ x \lt 1 \end{array} \right.} \\ {\left\{ \begin{array}{c} x \lt -5 \\ x \gt 1 \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} -5 \lt x \lt 1 \\ x \in \varnothing \end{array} \right. $$

Получаем: $-5 \lt x \lt 1 $

Целые решения из найденного интервала:

$ x \in \{-4;-3;-2;-1;0\} $

Пример 4. Решите неравенство: $x^2+3|x|-4 \lt 0$

Замена переменных: $ {\left\{ \begin{array}{c} t = |x| \\ t^2+3t-4 \lt 0 \end{array} \right.} $

Решаем: $t^2+3t-4 \lt 0 \iff (t+4)(t-1) \lt 0 \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} t+4 \gt 0 \\ t-1 \lt 0 \end{array} \right.} \\ {\left\{ \begin{array}{c} t+4 \lt 0 \\ t-1 \gt 0 \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} t \gt -4 \\ t \lt 1 \end{array} \right.} \\ {\left\{ \begin{array}{c} t \lt -4 \\ t \gt 1 \end{array} \right.} \end{array} \right. \iff$

$\iff \left[ \begin{array}{cc} -4 \lt t \lt 1 \\ t \in \varnothing \end{array} \right. \iff -4 \lt t \lt 1$

Возвращаемся к исходной переменной:

$ -4\lt |x|\lt 1 \iff |x|\lt 1 \iff -1\lt x\lt 1 $

Ответ: $x \in (-1;1)$