Понятие алгебраической дроби. Основное свойство

Определение алгебраической дроби

Чтобы дать определение алгебраической дроби, необходимо повторить, что такое алгебраическое выражение (см. §1 справочника для 7 класса) и многочлен (см. §14 справочника для 7 класса).

Алгебраическая дробь, как и другие алгебраические выражения, может быть рациональной или иррациональной. Напомним, что в иррациональных выражениях извлекаются корня из переменных (или переменные возводятся в степень с дробным показателем). В рациональных выражениях корни и дробные степени или вообще не извлекаются или извлекаются только из чисел.

Например: Дробь $\frac{x+5}{x-4}$ существует при условии x≠4. Допустимые значения переменной $\{x| x \in \Bbb R, x \neq 4 \} $.

Дробь $\frac{y}{y^2-9}$ существует при условии y≠±3. Допустимые значения переменной $ \{ y| y \in \Bbb R, y \neq \pm 3 \}$.

Основное свойство алгебраической дроби

Это свойство аналогично основному свойству обычной числовой дроби: мы можем одновременно умножать или делить числитель и знаменатель на любое выражение, сокращать на общий множитель, если он существует. Например:

$$ \frac{2x+3y}{4x^2-9y^2} = \frac{2x+3y}{(2x+3y)(2x-3y)} = \frac{1}{2x-3y} $$

$$ \frac{a^3-8}{a-2} = \frac{(a-2)(a^2+2a+4)}{a-2} = a^2+2a+4 $$

Приведение алгебраических дробей к общему знаменателю

Основное свойство алгебраических дробей позволяет приводить их к общему знаменателю и упрощать сложные выражения:

$$ \frac{1^{(x+1)}}{x-1} - \frac{1}{x^2-1} - \frac{1^{(x-1)}}{x+1} = \frac{x+1-1-(x-1)}{(x-1)(x+1)} = \frac{1}{x^2-1} $$

Например: привести к общему знаменателю $\frac{1}{xy^2}, \frac{x}{y}, \frac{-4}{x}$

Шаг 1. Наименьшее общее кратное: $xy^2$

Шаг 2. Дополнительные множители

$$ \frac{1}{xy^2}, \frac{x^{xy}}{y}, -\frac{4^{y2}}{x}$$

Шаг 3. Результат:

$$ \frac{1}{xy^2}, \frac{x^2 y}{xy^2}, -\frac{4y^2}{xy^2} $$

Перемена знака у члена дроби

Из основного свойства дроби следует, что одновременное умножение числителя и знаменателя на (-1) не изменит дробь:

$$ \frac{x}{y} = \frac{-x}{-y} $$

Дробь также не изменится, если провести следующие перемены знаков:

$$ \frac{x}{y} = \frac{-x}{y} = -\frac{x}{-y} $$

Ещё несколько полезных формул, связанных с переменой знаков:

$$ \frac{a-b}{b-a} = -1, \frac{(a-b)^2}{(b-a)^2} = 1, \frac{1}{a-b} = -\frac{1}{b-a}, \frac{1}{(a-b)^2} = \frac{1}{(b-a)^2} $$

Примеры

Пример 1. Найдите допустимые значения переменных, входящих в дробь:

а)$ \frac{5}{a^2-4}$

$ a^2-4 \neq 0 \iff (a-2)(a+2) \neq 0 \iff a \neq \pm 2$

$\{a| a \in \Bbb R, a \neq \pm 2\}$ - все действительные числа, кроме $\pm 2$

б)$ \frac{7x+y}{3x-1}$

$ 3x-1 \neq 0 \iff x \neq \frac{1}{3}$

$\{x|x \in \Bbb R, x \neq \frac{1}{3}\}$ - все действительные числа, кроме $\frac{1}{3}$

в)$ \frac{k^2-1}{k+1}$

$k+1 \neq 0 \iff k \neq -1 $

$\{k|k \in \Bbb R, k \neq -1\}$ - все действительные числа, кроме -1

Обратите внимание: несмотря на то, что дробь сокращается $\frac{k^2-1}{k+1} = \frac{(k+1)(k-1)}{k+1} = k-1$ требование $k \neq -1$ сохраняется.

г) $ \frac{5}{x^2+6x+9}$

$x^2+6x+9 \neq 0 \iff (x+3)^2 \neq 0 \iff x \neq -3 $

$ \{x|x \in \Bbb R, x \neq -3\}$ - все действительные числа, кроме -3

д)*$ \frac{1}{x-\frac{4}{x}} $

$$ x- \frac{4}{x} \neq 0 \iff \frac{x^2-4}{x} \neq 0 \iff {\left\{ \begin{array}{c} x^2-4 \neq 0 \\ x \neq 0 \end{array} \right.} \iff x \neq {0; \pm2}$$

$\{x|x \in \Bbb R, x \neq {0;\pm2}\}$ - все действительные числа, кроме $0,\pm2$

е)*$ \frac{5}{y^2-3|y|} $

$ y^2-3|y| \neq 0 \iff |y|(|y|-3) \neq 0 \iff {\left\{ \begin{array}{c} |y| \neq 0 \\ |y| \neq 3 \end{array} \right.} \iff y \neq {0; \pm3} $

$\{y|y \in \Bbb R, y \neq {0; \pm3} \}$ - все действительные числа, кроме $0, \pm3$

Пример 2. Сократите дроби:

а) $$ \frac{a^2-9}{2a+6} = \frac{(a-3)(a+3)}{2(a+3)} = \frac{a-3}{2}$$

б)$$ \frac{x^2+2x+1}{x^2-1} = \frac{(x+1)^2}{(x+1)(x-1)} = \frac{x+1}{x-1}$$

в) $$ \frac{12x^2-8xy}{3xy-2y^2} = \frac{4x(3x-2y)}{y(3x-2y)} = \frac{4x}{y} $$

г) $$ \frac{b+5}{b^3-125} = \frac{b+5}{(b+5)(b^2-5b+25)} = \frac{1}{b^2-5b+25} $$

Пример 3. Упростите выражение:

а) $$ \frac{a-b}{(b-a)^2} = \frac{a-b}{(a-b)^2} = \frac{1}{a-b}$$

б) $$ \frac{(-a-b)^2}{a+b} = \frac{(-1)^2 (a+b)^2}{a+b} = a+b $$

в) $$ \frac{(-a-b)^2}{(a+b)^2} = \frac{(a+b)^2}{(a+b)^2} = 1 $$

г) $$ \frac{(a-b)^2}{b-a} = \frac{(b-a)^2}{b-a} = b-a $$

Пример 4. Постройте график функции:

(О графике линейной функции – см. §38 справочника для 7 класса)

$а) y(x) = \frac{x^2-4}{2x+4}$

$$ y(x) = \frac{(x-2)(x+2)}{2(x+2)} = {\left\{ \begin{array}{c} \frac{x-2}{2} \\ x \neq -2 \end{array} \right.} $$

График – прямая y(x) = 0,5x-1, кроме точки (-2;-2), т.к. $x \neq -2$.

$б) y(x) = \frac{x^3-16x}{x^2-16}-2x+1$

$$ y(x) = \frac{x(x^2-16)}{x^2-16}-2x+1 = {\left\{ \begin{array}{c} -x+1 \\ x \neq \pm 4 \end{array} \right.} $$

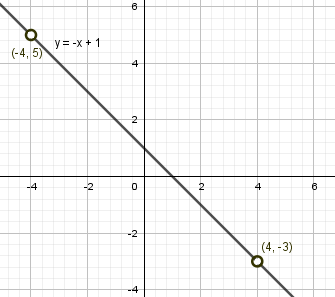
График – прямая y(x) = -x+1, кроме точек (-4;5) и (4;-3), т.к. $x \neq \pm 4$.