Главная Справочник Алгебра 8 класс Пересечение и объединение числовых промежутков

Пересечение и объединение числовых промежутков

Пример 1. Изобразите множества и их объединения на числовой прямой:

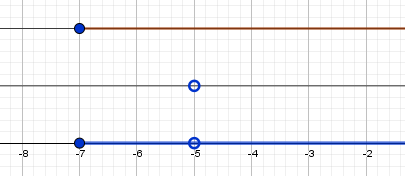
$ а) x \lt 1 \cup x \ge 3 $

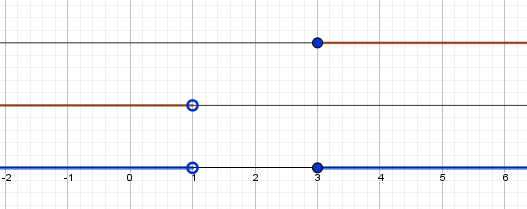
Пример 1 a)

$ б) -1 \lt x \lt 2 \cup 0 \lt x \lt 5 \iff -1 \lt x \lt 5$

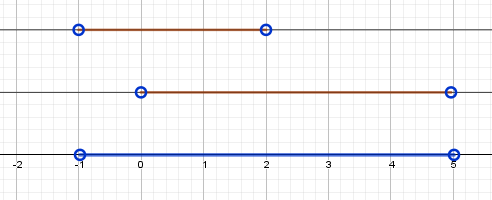
Пример 1 б)

$ в) x \gt 3 \cup x \lt 5 \iff x \in \Bbb R $ - вся числовая прямая

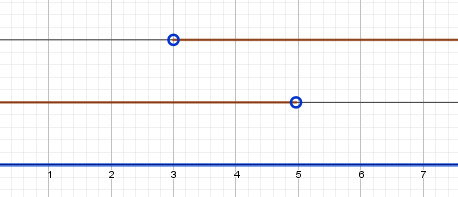
Пример 1 в)

$ г) -2 \lt x \lt 0 \cup 0 \lt x \lt 2 $

Пример 1 г)

Пример 2. Изобразите множества и их пересечения на числовой прямой:

$ а) x \lt 3 \cap x \ge 1 \iff 1 \le x \lt 3 $

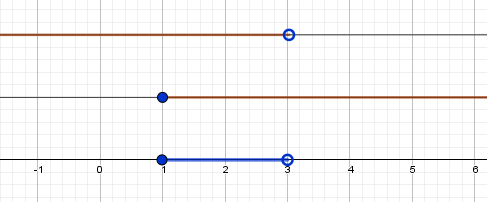
Пример 2. a)

$ б) -1 \lt x \lt 2 \cap 0 \le x \lt 5 \iff 0 \le x \lt 2$

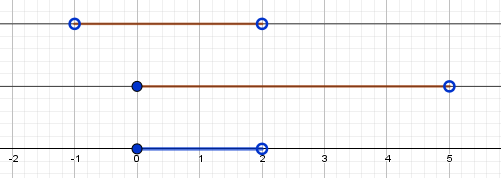
Пример 2. б)

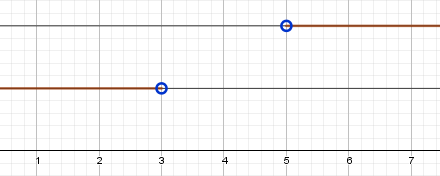
$ в) x \gt 5 \cap x \lt 3 \iff x \in \varnothing $ - вся числовая прямая

Пример 2. в)

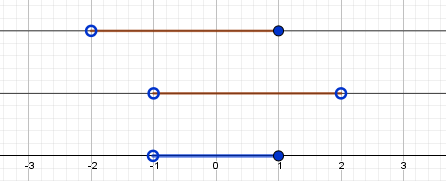
$ г) -2 \lt x \le 1 \cap -1 \lt x \lt 2 \iff -1 \lt x \le 1 $

Пример 2. г)

Пример 3. Найдите множество значений переменной, при которых выражение имеет смысл:

$ а) \sqrt x+ \sqrt{4-x}$

$ {\left\{ \begin{array}{c} x \ge 0 \\ 4-x \ge 0 \end{array} \right.} $

$ {\left\{ \begin{array}{c} x \ge 0 \\ x \le 4 \end{array} \right.} $

$ 0 \le x \le 4 $

$ x \in [0;4] $

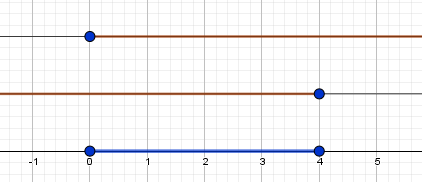
Пример 3. a)

$ б) \sqrt{x-3}+ \frac{1}{x-4} $

$ {\left\{ \begin{array}{c} x-3 \ge 0 \\ x \neq 4 \end{array} \right.} $

$ x \in [3;4) \cup (4;+ \infty) $

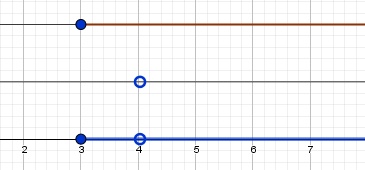
Пример 3. б)

$ в) \sqrt{2-x} + \frac{1}{\sqrt{x-4}}$

$ {\left\{ \begin{array}{c} 2-x \ge 0 \\ x-4 \gt 0 \end{array} \right.} $

$ {\left\{ \begin{array}{c} x \le 2 \\ x \gt 4 \end{array} \right.} $

$ x \in \varnothing$ - нет решений

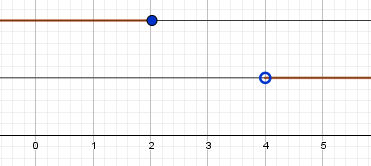
Пример 3. в)

$ г) \frac{1}{x+5} - \frac{1}{\sqrt{7+x}} $

$ {\left\{ \begin{array}{c} 7+x \ge 0 \\ x \neq -5 \end{array} \right.} $

$ {\left\{ \begin{array}{c} x \ge -7 \\ x \neq -5 \end{array} \right.} $

$ x \in [-7;-5) \cup (-5;+\infty) $

Пример 3. г)