Общий алгоритм построения графика функции с помощью преобразований

Алгоритм построения графика функции с помощью преобразований

На входе функция

$$y = af(kx+b)+c, \quad a \neq 0 , \quad k \neq 0$$

которая базируется на исходной функции y=f(x).

Шаг 1. Выполнить преобразования аргумента:

• 1.1. С коэффициентом k - растяжение (сжатие) по оси OX

  (см. §47 данного справочника)

• 1.2. С параметром b – сдвиг влево/вправо по оси OX

  (см. §48 данного справочника)

Шаг 2. Выполнить преобразования функции:

• 2.1. С коэффициентом a - растяжение (сжатие) по оси OY

  см. §47 данного справочника)

• 2.2. С параметром c – сдвиг вверх/вниз по оси OY

  (см. §48 данного справочника)

Примеры

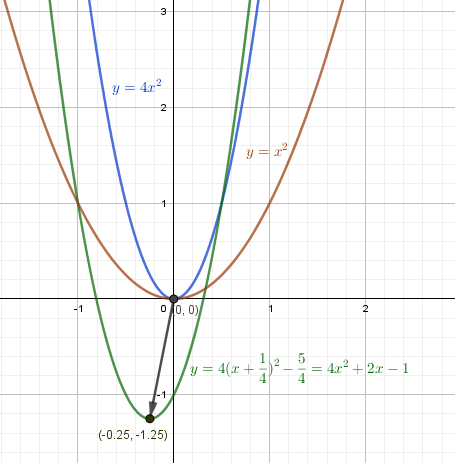
Пример 1. Постройте график функции $y = 4x^2+2x-1$

Функция – квадратный трёхчлен ( см. §29 данного справочника)

Строим параболу. Выделяем полный квадрат

$$ y = \Biggl((2x)^2+2 \cdot 2x \cdot \frac{1}{2} + \left(\frac{1}{2}\right)^2 \Biggr) -1-\left(\frac{1}{2}\right)^2 = \left(2x+ \frac{1}{2}\right)^2- \frac{5}{4} = 4 \left(x+ \frac{1}{4} \right)^2- \frac{5}{4} $$

Коэффициент 2 сжимает функцию $y = x^2$ в два раза по оси OX в $y = (2x)^2 = 4x^2$

Параметр $\frac{1}{4}$ сдвигает вершину на $\frac{1}{4}$ влево.

Параметр $-\frac{5}{4}$ опускает вершину на $\frac{5}{4}$ вниз.

Получаем параллельный перенос вершины $y = (2x)^2$ из (0;0) в $(-\frac{1}{4}; -\frac{5}{4})$.

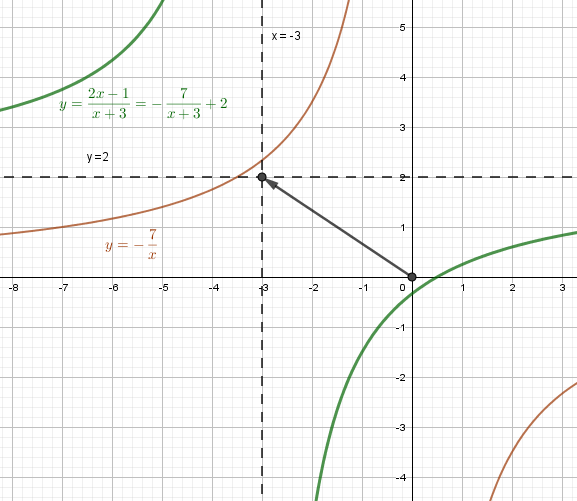
Пример 2. Постройте график функции $y = \frac{2x-1}{x+3} $

Функция – дробно-линейная (см. §49 данного справочника)

Выделяем целую часть:

$$ y = \frac{2x-1}{x+3} = \frac{2x+6-7}{x+3} = \frac{2(x+3)-7}{x+3} = - \frac{7}{x+3} +2 $$

Базовая функция $y = -\frac{7}{x}$

Асимптоты x = -3, y = 2

Получаем: