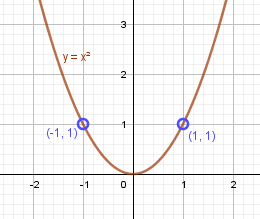
Функция y=x² и её график. Парабола
График функции y=x²
Составим таблицу для расчёта значений функции $y = x^2$:
|
x |
-3 |
-2,5 |
-2 |
-1,5 |
-1 |
-0,5 |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
|
$ y = x^2$ |
9 |
6,25 |
4 |
2,25 |
1 |
0,25 |
0 |
0,25 |
1 |
2,25 |
4 |
6,25 |
9 |
Отметим полученные точки на координатной плоскости и соединим их кривой:

Полученный график называют параболой. Точка (0;0) - это вершина параболы. Вершина делит график на левую и правую части, которые называют ветвями параболы.
Свойства параболы y=x²
1. Область определения $x \in (- \infty;+ \infty)$ - все действительные числа.
2. Область значений $y \in [0;+ \infty)$ - все неотрицательные действительные числа.
3. Функция убывает при $x \lt 0$, функция возрастает при $x \gt 0$.
4. Наименьшее значение функции y = 0 - в вершине параболы при x = 0. Вершина параболы совпадает с началом координат.
5. Все точки на ветвях параболы лежат выше оси абсцисс, для них $y \gt 0$.
6. График параболы симметричен относительно оси ординат, противоположным значениям аргумента соответствует одно и то же значение функции:
$$ (-x)^2 = x^2 \Rightarrow y(-x) = y(x) $$
В таких случаях говорят, что функция чётная.
Примечание:
Если использовать запись для множеств и их элементов (см.§8 данного справочника), то область определения можно записать как $\{x|x \in \Bbb R\}$, а область значений $\{y|y \ge 0, y \in \Bbb R\}$.
Примеры
Пример 1. Решите графически уравнение:
а) $x^2 = 4x$
$y = x^2$
y = 2x
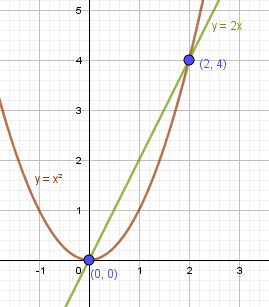
Ответ: $x_1 = 0, x_2 = 2$
б) $x^2 = \frac{4}{x}$
$y = x^2$
$y = \frac{8}{x}$

Ответ: x = 2
в) $x^2 = -2x+3$
$y = x^2$
y = -2x+3

Ответ: $x_1 = -3, x_2 = 1$
г) $x^2 = 4$
$y = x^2$
y = 4

Ответ: $x_1 = -2, x_2 = 2$
Пример 2. Постройте график функции:
а) $y = \frac{x^3+2x^2}{x+2} $
$$ y = \frac{x^3+2x^2}{x+2} = \frac{x^2 (x+2)}{x+2} \iff {\left\{ \begin{array}{c} y = x^2 \\ x \neq -2 \end{array} \right.} $$
График – это функция $y = x^2$, кроме одной точки с $x \neq -2$.
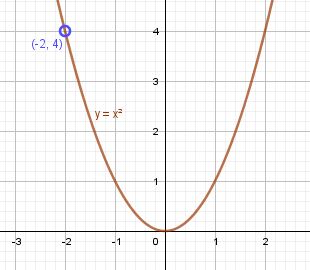
б)$ y = \frac{x^2-x^4}{1-x^2}$
$$ y = \frac{x^2-x^4}{1-x^2} = \frac{x^2 (1-x^2 )}{1-x^2} \iff {\left\{ \begin{array}{c} y = x^2 \\ x \neq \pm 1 \end{array} \right.} $$
График – это функция $y = x^2$, кроме двух точек с $ x \neq \pm 1 $.