Способы решения линейных диофантовых уравнений с двумя переменными
Рассмотрим способы решения уравнений вида $ax + by = c$ с целыми коэффициентами $a\mathbb{\in Z,\ }b\mathbb{\in Z}$, целым свободным членом $c\mathbb{\in Z}$ в целых числах $x\mathbb{\in Z,}y\mathbb{\in Z}$.
Такие уравнения называются диофантовыми.
Пусть нам необходимо решить уравнение
| $6x+7y=59$, $x\mathbb{\in Z,}$ $y\mathbb{\in Z}$ | (1) |
Способ 1. Строгое получение общего решения выделением целой части в дробном выражении
Выразим \(x\) через \(y,\) выделим целую часть в полученной дроби
\[x = \frac{59 - 7y}{6} = \frac{60 - 1 - 6y - y}{6} = 10 - y - \frac{1 + y}{6}\]
Чтобы \(x\) был целым, \((1 + y)\) должно быть кратно 6
\(1 + y = 6k,\ \)где \(k\mathbb{\in Z}\) - любое целое число. Тогда
\[x = 10 - y - \frac{6k}{6} = 10 - y - k \Longleftrightarrow y = 10 - x - k\]
С другой стороны, \(y = \frac{59 - 6x}{7}\). Получаем уравнение для \(x\)
\[\frac{59 - 6x}{7} = 10 - x - k\]
\[59 - 6x = 70 - 7x - 7k\]
\[x = 11 - 7k\]
Тогда
\[y = 10 - (11 - 7k) - k = - 1 + 6k\]
Общее решение
| \[\left\{ \begin{matrix} x = 11 - 7k \\ y = - 1 + 6k \\ \end{matrix} \right.\ ,\ \ k\mathbb{\in Z}\ \] |
Множество способов позволяют подобрать частное решение уравнения (1), и затем записать общее решение. Чтобы найти шаг, на который изменяются x и y, действуем по следующему алгоритму.
Допустим, мы подобрали частное решение \((x_{0},y_{0})\). Тогда
\[6x_{0} + 7y_{0} = 59\ |:(6 \cdot 7 = 42)\]
\[\frac{x_{0}}{7} + \frac{y_{0}}{6} = \frac{59}{42}\]
Если мы хотим из частного решения получить общее решение, то x должен изменяться с шагом 7m в одну сторону (например, уменьшения) y - с шагом 6m в другую сторону. Действительно
\[\frac{x_{0} - 7m}{7} + \frac{y_{0} + 6m}{6} = \frac{x_{0}}{7} - m + \frac{y_{0}}{6} + m = \frac{x_{0}}{7} + \frac{y_{0}}{6} = \frac{59}{72}\]
Т.е., для любого найденного частного решения \(\left( x_{0},y_{0} \right)\ \)уравнения (1) общее решение имеет вид
\[\left\{ \begin{matrix} x = x_{0} - 7m \\ y = y_{0} + 6m \\ \end{matrix} \right.\ \]
где \(m\mathbb{\in Z}\) - любое целое число.
Рассмотрим некоторые из способов подбора частного решения.
Способ 2. Подбор частного решения по соотношению Безу
Т.к. 6 и 7 - взаимно простые числа, по соотношению Безу существуют такие целые \(a\ и\ b\), что
\[6a + 7b = 1\]
Элементарным подбором находим
\[6 \cdot ( - 1) + 7 \cdot 1 = 1\]
Чтобы получить уравнение (1), умножаем на 59
\[6 \cdot ( - 59) + 7 \cdot 59 = 59\]
Таким образом, получаем частное решение
\[x_{0} = - 59,\ \ y_{0} = 59\]
Серия решений определяется с тем де шагом
| \[\left\{ \begin{matrix} x = - 59 - 7m \\ y = 59 + 6m \\ \end{matrix} \right.\ ,\ \ m\mathbb{\in Z}\ \] |
Если сравнить решения, полученные Способом 2 и Способом 1, во втором случае \(x\ и\ y\) сдвинуты на 10 шагов. Для \(m = k + 10\)
\[\left\{ \begin{matrix} x = - 59 - 7(k + 10) = 11 - 7k \\ y = 59 + 6(k + 10) = - 1 + 6k \\ \end{matrix} \right.\ ,\ \ k\mathbb{\in Z}\]
Получаем предыдущее решение.
Способ 3. Подбор частного решения по дроби
Т. к. \(x = \frac{59 - 7y}{6} = 10 - y - \frac{1 + y}{6}\), решаем уравнение
\[\frac{1 + y}{6} = 1 \Longleftrightarrow y = 6 - 1 = 5\]
Тогда \(x = \frac{59 - 7 \cdot 5}{6} = 4\)
Получаем частное решение
\[x_{0} = 4,\ \ y_{0} = 5\]Записываем общее решение
| \[\left\{ \begin{matrix} x = 4 - 7m \\ y = 5 + 6m \\ \end{matrix} \right.\ ,\ \ m\mathbb{\in Z}\ \] |
Если сравнить решения, полученные Способом 3 и Способом 1, в третьем случае x и y сдвинуты на 1 шаг. Для \(m = k - 1\)
\[\left\{ \begin{matrix} x = 4 - 7(k - 1) = 11 - 7k \\ y = 5 + 6(k - 1) = - 1 + 6k \\ \end{matrix} \right.\ ,\ \ k\mathbb{\in Z}\]
Получаем предыдущее решение.
Способ 4. Подбор частного решения по кругу с секторами
По соотношению Безу существуют такие целые \(a\ и\ b\), что
\[6a + 7b = 1\]
Разделим уравнение на больший коэффициент
\[6a + 7b = 1\ |:7,\ \ \frac{6}{7}a + b = \frac{1}{7},\ \ b = \frac{1}{7} - \frac{6}{7}a = 1 + \frac{6}{7}( - a)\]
Разбиваем круг на 7 равных секторов, определяем одну из точек на окружности как начало отсчёта. Определяем движение по часовой стрелке как положительное направление.
Сдвигаемся по часовой стрелке на \(\frac{1}{7}\) от начала отсчета.
Теперь от точки \(\frac{1}{7}\) ходим по кругу по часовой или против часовой стрелки на \(\frac{6}{7}a\) (по шесть точек за шаг) так, чтобы попасть в начало отсчета. И считаем количество шагов \(a\). Если двигаемся по часовой стрелке, то \(a < 0;\) если против часовой стрелки, то \(a > 0\), т.к. коэффициент при \(a\) отрицательный.
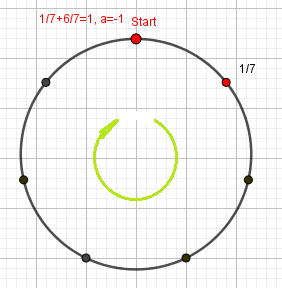 4а |
Если пойдем по часовой стрелке, то уже после первого шага (через 6 точек) окажемся в начале отсчета. Значит, \(a_{0} = - 1\). Тогда \(b_{0} = \frac{1}{7} + \frac{6}{7} = 1\) Получаем уравнение \[6 \cdot ( - 1) + 7 \cdot 1 = 1\] Далее - решение аналогично способу 2. Ответ
|
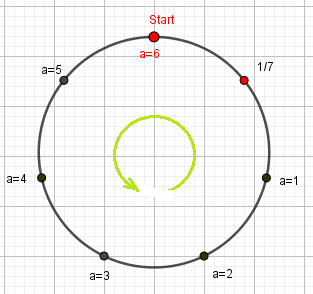 4б |
Если пойдем против часовой стрелки, то окажемся на старте через 6 шагов. \[a_{0} = 6\] \[b_{0} = \frac{1}{7} - 6 \cdot \frac{6}{7} = - \frac{35}{7} = - 5\] Получаем уравнение \[6 \cdot 6 + 7 \cdot ( - 5) = 1\] Чтобы получить уравнение (1), умножаем на 59 \[6 \cdot (6 \cdot 59) + 7 \cdot ( - 5 \cdot 59) = 59\] Найдено частное решение \[x_{0} = 6 \cdot 59 = 354\] \[y_{0} = - 5 \cdot 59 = - 295\] Ответ
|
Если сравнить решения, полученные Способом 4б и Способом 1, в последнем случае \(x\ и\ y\) сдвинуты на 49 шагов. Для \(m = k + 49\)
\[\left\{ \begin{matrix} x = 354 - 7(k + 49) = 11 - 7k \\ y = - 295 + 6(k + 49) = - 1 + 6k \\ \end{matrix} \right.\ ,\ \ k\mathbb{\in Z}\]
Получаем предыдущее решение.


