Прямоугольная система координат на плоскости
Координатная плоскость
Две взаимно перпендикулярные прямые с выбранными направлениями и единицей длины называются осями координат и образуют прямоугольную систему координат на плоскости.
Плоскость, на которой выбрана система координат, называют координатной плоскостью.

Прямые углы, образованные осями координат, называют координатными углами (или квадрантами).
Их нумеруют так, как показано на рисунке слева.
Любую точку на координатной плоскости можно задать с помощью двух координат: абсциссы x и ординаты y.

График функции
Графиком функции называется множество точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.
Ниже представлены графики функций, формулы для которых найдены в примере 1 §34 данного справочника.
а) $S = a^2$
$ a \ge 0$ – сторона квадрата (см),
S- площадь ($см^2$)
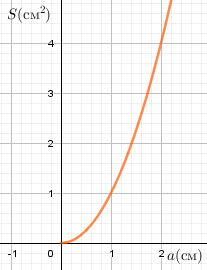
б) P = 2(a+5)
$a \ge 0$ – одна из сторон прямоугольника (см),
P – периметр (см)

в) S=1,1d
$d \ge 0$ - сумма депозита (тыс.руб.),
S - конечная сумма к выплате (тыс.руб.)
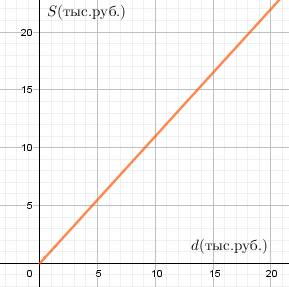
г) s = 10+40t
$t \ge 0$ – время (ч),
s - расстояние (км)
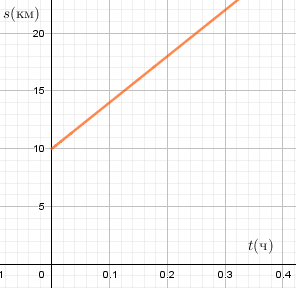
Как видно из представленных графиков, по осям могут откладываться совершенно разные величины, в разном масштабе.
Большую роль при построении графиков играет область определения функции. В данном случае все аргументы – время, длина, вложенные деньги – неотрицательны ($\ge 0$).
Внимание!
Иллюстрируя с помощью графиков различные явления, хорошо продумывайте единицы измерения и масштаб по каждой из координатных осей.
Не забывайте указывать единицы измерения и значения делений на осях.
Примеры
Пример 1. Вспомните определение функции (см. §34 данного справочника) и скажите, какая из кривых может быть графиком функции, какая – не может, и почему?
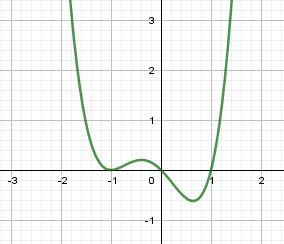
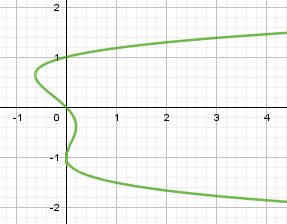
По определению функции каждому аргументу соответствует единственное значение функции.
На кривой слева каждому x соответствует единственный y. Поэтому кривая слева – график функции.
На кривой справа каждому значению x (кроме минимального слева) соответствуют два и больше значений y: например при x = 0, y = $\{0; \pm 1\}$ – три значения y. Поэтому кривая справа не является графиком функции.
Пример 2. Известно, что тормозной путь автомобиля, движущегося со скоростью v, равен $s = \frac{v^2}{2μg}$, где g ≈ 10 $\frac{м}{с^2}$ - ускорение свободного падения, μ – коэффициент сцепления шин с дорогой. В разных погодных условиях μ равен:
Сухой асфальт
Мокрый асфальт
Гололёд
0,7
0,4
0,1
Постройте кривые зависимости тормозного пути (в метрах) от скорости в начале торможения (в м/с) в разных погодных условиях.
Найдите, чему равен тормозной путь при начальной скорости v = 54 $\frac{км}{ч}$ = 15 $\frac{м}{с}$ в каждом из трёх случаев.
Рассчитаем параметр 2μg для каждого случая:
Сухой асфальт
Мокрый асфальт
Гололёд
$s_1 = \frac{v^2}{14}$
$s_2 = \frac{v^2}{8}$
$s_3 = \frac{v^2}{2}$
Составим таблицу для построения графиков:
|
v, м/с |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
|
$s_1$,м |
0 |
0,29 |
1,14 |
2,57 |
4,57 |
7,14 |
10,29 |
14,00 |
18,29 |
23,14 |
|
$s_2$,м |
0 |
0,5 |
2 |
4,5 |
8 |
12,5 |
18 |
24,5 |
32 |
40,5 |
|
$s_3$, м |
0 |
2 |
8 |
18 |
32 |
50 |
72 |
98 |
128 |
162 |
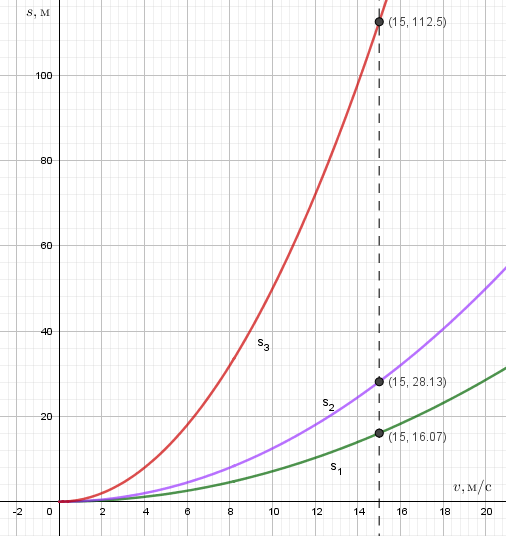
Тормозной путь при v = 15 $\frac{м}{с}$
Сухой асфальт
Мокрый асфальт
Гололёд
16,07 м
28,13 м
112,5 м
Будьте осторожны на дорогах!


