Линейное уравнение с двумя переменными и его график
График линейного уравнения с двумя переменными
В линейном уравнении с двумя переменными ax+by=c , a и b называют коэффициентами при переменных, c - свободным членом.
Действительно:
$$ ax+by = c \iff y = - \frac{a}{b} x+ \frac{c}{b} $$
Если сравним полученное уравнение $с y = kx+ \tilde b$ (см. §38 данного справочника), получаем:
$$ k = -\frac{a}{b} , \tilde b = \frac{c}{b}$$
Графиком $y = kx+ \tilde b$ является прямая, угловой коэффициент k определяет угол наклона, слагаемое $\tilde b$ – точку пересечения прямой с осью Y (см. §39 данного справочника).
Точки пересечения с осями координат:
${\left\{ \begin{array}{c} x = 0 \\ y = \frac{c}{b}\end{array} \right.}, {\left\{ \begin{array}{c} x = \frac{c}{a} \\ y = 0\end{array} \right.}$

Внимание!
График линейной функции ax+by=c с ненулевыми коэффициентами очень удобно чертить по двум точкам пересечения с осями координат: точка на оси X ( $\frac{c}{a}$;0) и точка на оси Y (0; $\frac{c}{b}$)
Равенство нулю коэффициентов при переменных:
$0x+2y = 4 \Rightarrow y = 2$

График – прямая, параллельная оси Х.
$3x+0y = 3 \Rightarrow x = 1$

График – прямая, параллельная оси У.
a = 0, b = 0, c = 0
a = 0, b = 0, $c \neq 0$
0x+0y = 0
x, $y \in \Bbb R$ - любое действительное число.
График – вся координатная плоскость
0x+0y = 5
Решений нет.
График – пустое множество.
Взаимное расположение графиков двух уравнений
$$ a_1 x+b_1 y = c_1 и a_2 x+b_2 y = c_2 $$

Прямые пересекаются

Прямые параллельны

Прямые совпадают
Примеры
Пример 1. Постройте график линейного уравнения по двум точкам пересечения с осями.
а) 2x-y = 6
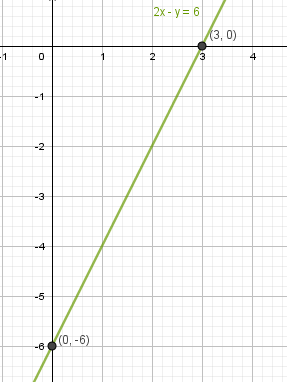
б) 1,5x+y = 3

в) x+y = -2
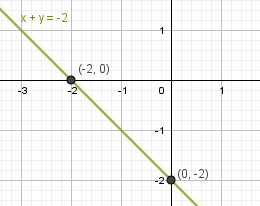
г) x-3y = 6
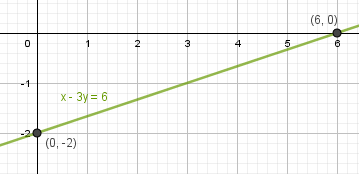
Пример 2. Постройте в одной координатной плоскости графики, найдите точку пересечения:
а) x+2y = 4 и x-2y = 4
Точка пересечения (4;0)

б) x+y = 4 и x-y = -1
Точка пересечения (1,5;2,5)



