Закон больших чисел и центральная предельная теорема
п.1. Теорема Бернулли
Т.е., при большом количестве испытаний частота события стремится к его вероятности и перестает быть случайной.
Например, если число бросаний монеты \(n\rightarrow\infty\), то отношение \(\frac{k_n}{n}\rightarrow\frac12\), число выпадения орлов в этом пределе равно половине всех испытаний.
Теорема Бернулли – это частный случай закона больших чисел.
п.2. Неравенство Чебышева
Неравенство Чебышева дает оценку верхней границы для вероятности отклонения величины от её среднего значения; или оценку нижней границы вероятности того, что величина попадет в ε-окрестность её среднего значения.
Что интересно, распределение величины x при этом может быть неизвестно.
Достаточно знать \(D(x)\).
Например:
Пусть дисперсия случайной величины равна \(D(x)=1,5\). Оценим вероятность того, что случайная величина не отклонится от среднего значения больше, чем на \(\varepsilon=2\).
Ищем оценку: \(P(|x-M(x)|\lt\varepsilon)\geq 1-\frac{D(x)}{\varepsilon^2}\)
\(P(|x-M(x)|\lt 0,1)\geq 1-\frac{1,5}{2^2}=1-\frac38=\frac58=0,625\)
\(P\geq 0,625\)
п.3. Неравенство Маркова
Pаспределение величины x при этом может быть неизвестно.
Достаточно знать \(M(x)\).
Например:
Пусть в среднем ученики опаздывают на 2 минуты. Какова вероятность, что ученик опоздает более чем на 10 минут?
В данном случае \(\varepsilon=10,\ M(x)=2\). Получаем оценку вероятности:
\(P(x\geq \varepsilon)\leq \frac{M(x)}{\varepsilon}\)
\(P(x\geq 10)\leq \frac{2}{10}=0,2\)
\(P\leq 0,2\)
п.4. Закон больших чисел
Под законом больших чисел в широком смысле понимается общий принцип, согласно которому, по формулировке А.Н. Колмогорова, совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.
Т.е., при большом числе случайных величин их средняя величина перестает быть случайной и может быть предсказана с большой степенью определенности.
Под законом больших чисел в узком смысле понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа опытов к определенным постоянным, неслучайным величинам.
Если последовательность \(x_1,x_2,…,x_n\) является независимыми случайными величинами с мат. ожиданием \(M(x)\) и ограниченной дисперсией \(D(x)\), то для любого малого \(\varepsilon\gt 0\) справедливо: $$ \lim_{n\rightarrow\infty}P\left(\left|\frac1n\sum_{i=1}^n x_i-M(x)\right|\lt\varepsilon\right)=1 $$
В более широкой формулировке (для зависимых случайных величин и разных мат.ожиданий):
Если для последовательности случайных величин \(x_1,x_2,…,x_n\) $$ \lim_{n\rightarrow\infty}\frac{1}{n^2}D \left(\sum_{i=0}^n x_i\right)=0 $$ то среднее арифметическое наблюдаемых значений сходится к среднему арифметическому их мат.ожиданий: $$ \lim_{n\rightarrow\infty}P\left(\left|\frac1n\sum_{i=1}^n x_i-\frac1n\sum_{i=1}^n M(x)\right|\lt\varepsilon\right)=1 $$
п.5. Стандартное нормальное распределение
Наиболее простым случаем нормального распределения является стандартное нормальное распределение N(0;1) со средней \(\mu=0\) и дисперсией \(\sigma^2=1\).
Плотность распределения в этом случае: $$ \varphi(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} $$ В MS Excel для плотности стандартного нормального распределения используется встроенная функция НОРМРАСП(x;0;1;0).
График плотности распределения N(0;1):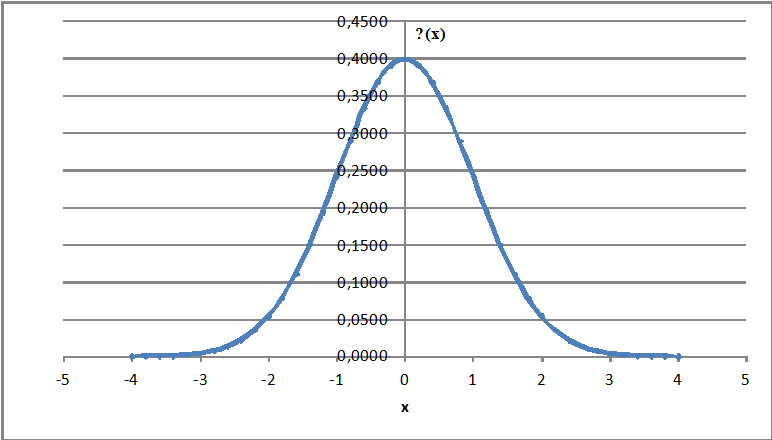
Функция распределения N(0;1): $$ F_0(x)=\int_{-\infty}^x \varphi(x)dx=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^x e^{=\frac{x^2}2}dx $$ В MS Excel для функции стандартного нормального распределения используется встроенная функция НОРМРАСП(x;0;1;1).
График функции распределения N(0;1):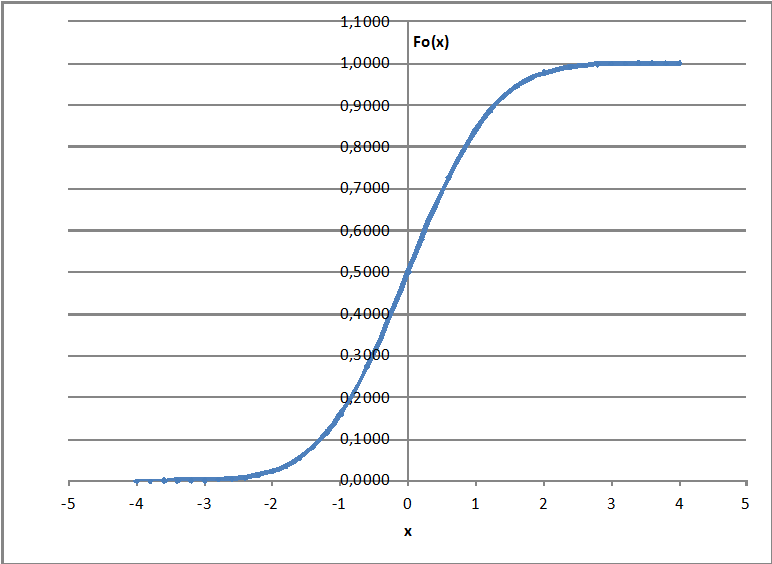
Исторически сложилось так, что для расчетов часто используется функция Лапласа: $$ Ф(x)=F_0(x)-\frac12 $$ 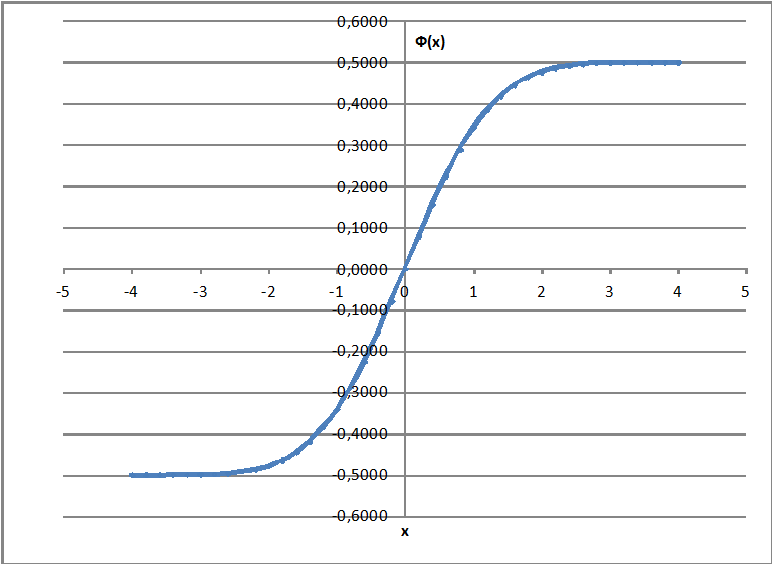
Её преимуществом является нечетность: \(Φ(-x)=-Φ(x).\)
Т.е., если у вас под рукой нет MS Excel, но есть таблица, то там, скорее всего, будет функция Лапласа \(Φ(x)\) для \(x\geq 0\), а не функция распределения \(F_0(x)\) для \(x\in\mathbb{R}\).
п.6. Центральная предельная теорема
Законы больших чисел не учитывают формы распределения случайных величин.
Центральная предельная теорема устанавливает условия, при которых распределение случайных величин стремится к нормальному.
Частными случаями ЦПТ являются теоремы Муавра-Лапласа.
При большом числе испытаний по схеме Бернулли распределение вероятностей стремится к нормальному. Вероятность того, что событие наступит в точности k раз, может быть вычислена по формуле: $$ P(X=k)\approx\frac{1}{\sqrt{npq}}\varphi(x),\ \ \text{где}\ x=\frac{k-np}{\sqrt{npq}} $$
Например:
Вероятность рождения мальчика равна \(p=0,51\). Найдем вероятность того, что среди 100 новорожденных окажется ровно 50 мальчиков.
По условию: \(n=100;\ k=50\)
Тогда: \(\mu=np=100\cdot 0,51=51\)
\(\sigma=\sqrt{npq}=\sqrt{100\cdot 0,51\cdot 0,49}=\sqrt{24,99}\)
\(x=\frac{k-\mu}{\sigma}=\frac{50-51}{\sqrt{24,99}}\approx -0,20004\)
Используя функцию MS Excel НОРМРАСП(x;0;1;0), получаем:
\(\varphi(x)\approx 0,3910\)
\(P(50)\approx \frac{0,3910}{\sqrt{24,99}}\approx 0,0782\)
При большом числе испытаний по схеме Бернулли распределение вероятностей стремится к нормальному. Вероятность того, что событие наступит от \(k_1\) до \(k_2\) раз, может быть вычислена по формуле: \begin{gather*} P(k_1\leq X\leq k_2)\approx Ф\left(\frac{k_2-np}{\sqrt{npq}}\right)-Ф\left(\frac{k_1-np}{\sqrt{npq}}\right)=\\ =F_0\left(\frac{k_2-np}{\sqrt{npq}}\right)-F_0\left(\frac{k_1-np}{\sqrt{npq}}\right) \end{gather*}
Очевидно, что разность двух значений функций Лапласа равна разности двух значений функций распределения.
Если у вас под рукой MS EXCEL, используйте НОРМРАСП(x;0;1;1), т.е. функцию распределения \(F_0(x)\).
Если у вас под рукой таблицы, используйте \(Φ(x)\), т.е. функцию Лапласа и её нечетность.
Например:
Найдем вероятность того, что при подбрасывании монеты 500 раз орел выпадет от 240 до 255 раз.
По условию: \(n=500;\ k_1=240;\ k_2=255\)
Для подбрасывания монеты \(p=\frac12\)
Тогда: \(\mu=np=500\cdot\frac12=250\)
\(\sigma=\sqrt{npq}=\sqrt{500\cdot \frac12\cdot \frac12}=5\sqrt{5}\)
\(x_1=\frac{k_1-\mu}{\sigma}=\frac{240-250}{5\sqrt{5}}=-\frac{10}{5\sqrt{5}}=-\frac{2}{\sqrt{5}}\)
\(x_2=\frac{k_2-\mu}{\sigma}=\frac{255-250}{5\sqrt{5}}=\frac{5}{5\sqrt{5}}=\frac{1}{\sqrt{5}}\)
Используя функцию MS Excel НОРМРАСП(x;0;1;1), получаем:
\(P(240\leq X\leq 255)\approx F_0(x_2)-F_0(x_1)=0,6727-0,1855=0,4871\)
п.7. Примеры
Пример 1. Ежегодная потребность школы в электроэнергии равна 400 кВт·ч. Какой расход электроэнергии в будний день можно наблюдать с вероятностью не менее 0,8?
Будних дней в течение года 250.
Среднее потребление электроэнергии в будний день: \(M(x)=\frac{400}{250}=1,6\) кВт—ч/день
По неравенству Маркова:
\(P(x\lt\varepsilon)\geq 1-\frac{M(x)}{\varepsilon}=0,8\)
\(\frac{M(x)}{\varepsilon}=0,2\) \(\varepsilon=\frac{M(x)}{0,2}=\frac{1,6}{0,2}=8\)
Откуда \(x\lt 8\) кВт·ч/день
Ответ: с вероятностью 0,8 ежедневный расход не будет превышать 8 кВт·ч/день
Пример 2. Дисперсия потребления электроэнергии школой в будний день составляет \(D(x)=7\) (кВт·ч/день)2. Какой расход электроэнергии в будний день можно наблюдать с вероятностью не менее 0,8 при среднем потреблении \(M(x)=1,6\) кВт·ч/день?
По неравенству Чебышева:
\(P(|x-M(x)|\lt\varepsilon)\geq 1-\frac{D(x)}{\varepsilon^2}\)
\(P(|x-1,6|\lt\varepsilon)\geq 1-\frac{7}{\varepsilon^2}=0,8\)
\(\frac{7}{\varepsilon^2}=0,2\)
\(\varepsilon=\sqrt{\frac{7}{0,2}}=\sqrt{35}\approx 5,9\)
Интервал энергопотребления: \(M(x)-\varepsilon\lt x\lt M(x)+\varepsilon\)
\(1,6-5,9\lt x\lt 1,6+5,9\)
Потребление может быть только положительным \(x\gt 0\).
Получаем: \(0\lt x\lt 7,5\)
Ответ: с вероятностью 0,8 ежедневный расход находится в интервале \(0\lt x\lt 7,5\) кВт·ч/день
Пример 3. Страховая компания заключила 50000 договоров. Вероятность страхового случая по каждому из них в течение года равна 2%. Найти вероятность того, что таких случаев будет:
а) ровно 950;
б) не более 1000;
в) сколько случаев будет с вероятностью 0,9?
a) По условию: \(n=50000;\ p=0,02;\ k=950\)
Тогда: \(\mu=np=50000\cdot 0,02=1000\)
\(\sigma=\sqrt{npq}=\sqrt{50000\cdot 0,02\cdot 9,98}=\sqrt{980}=14\sqrt{5}\)
\(x=\frac{k-\mu}{\sigma}=\frac{950-1000}{14\sqrt{5}}=-\frac{5\sqrt{5}}{7}\)
Используя функцию MS Excel НОРМРАСП(x;0;1;0), получаем:
\(\varphi(x)\approx 0,1114\)
\(P(950)\approx\frac{0,1114}{14\sqrt{5}}\approx 0,0036\)
б) \(k_1=0;\ k_2=1000\)
\(x_1=\frac{k_1-\mu}{\sigma}=\frac{0-1000}{14\sqrt{5}}=-\frac{100\sqrt{5}}{7}\)
\(x_2=\frac{k_2-\mu}{\sigma}=\frac{1000-1000}{14\sqrt{5}}=0\)
Используя свойства функции распределения, получаем:
\(P(0\leq x\leq 1000)=F_0(0)-F_0\left(-\frac{100\sqrt{5}}{7}\right)\approx 0,5-0=0,5\)
в) По неравенству Чебышева:
\(P(|x-M(x)|\lt\varepsilon)\geq 1-\frac{D(x)}{\varepsilon^2}\)
\(M(x)=\mu=1000;\ D(x)=\sigma^2=980\)
\(P(|x-1000|\lt\varepsilon)\geq 1-\frac{980}{\varepsilon^2}=0,9\)
\(\frac{980}{\varepsilon^2}=0,1\)
\(\varepsilon-\sqrt{\frac{980}{0,1}}=\sqrt{9800}=70\sqrt{2}\)
Интервал страховых случаев: \(M(x)-\varepsilon\lt x\lt M(x)+\varepsilon\)
\(1000-70\sqrt{2}\lt x\lt 1000 +70\sqrt{2}\)
\(901\lt x\lt 1099\)
С вероятностью 0,9 страховых случаев будет от 901 до 1099.


