Главная Справочник Алгебра 10-11 класс Тангенс и котангенс на единичной числовой окружности

Тангенс и котангенс на единичной числовой окружности

Тангенс и котангенс острого угла в прямоугольном треугольнике
Базовые формулы тригонометрии
Тангенс и котангенс угла на числовой окружности
Знаки тангенса и котангенса
Тангенсы и котангенсы углов $\frac{\pi k}{2}$
Тангенсы и котангенсы углов $\frac{\pi}{4}+\frac{\pi k}{2}$
Тангенсы и котангенсы углов $\frac{\pi}{6}+\frac{\pi k}{2}$
Тангенсы и котангенсы углов $\frac{\pi}{3}+\frac{\pi k}{2}$
Примеры

п.1. Тангенс и котангенс острого угла в прямоугольном треугольнике

Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему.
tgα = $\frac{a}{b} $
Котангенс острого угла в в прямоугольном треугольнике равен отношению прилежащего катета к противолежащему.
ctgα = $\frac{b}{a} $

Например:

B ΔABC, ∠C = 90°, a = 2, b = 4. Найдем тангенс и котангенс ∠A. $$ tgA=\frac{a}{b}=\frac{2}{4}=\frac{1}{2},\ \ ctgA=\frac{b}{a}=\frac{4}{2}=2 $$

п.2. Базовые формулы тригонометрии

На данном этапе изучения тригонометрии получаем четыре базовых формулы:

\begin{gather*} sin^2\alpha+cos^2\alpha=1,\ \ tg\alpha\cdot ctg\alpha=1\\ tg\alpha=\frac{sin\alpha}{cos\alpha},\ \ ctg\alpha=\frac{cos\alpha}{sin\alpha} \end{gather*}

п.3. Тангенс и котангенс угла на числовой окружности

Построим вертикальную касательную к числовой окружности в точке A(1;0).
Продолжим луч OM до пересечения с касательной, обозначим точку пересечения E.
По построению: \begin{gather*} \begin{cases} \angle MKO=\angle EAO=90^{\circ}\\ \angle EOA - \text{общий (по двум углам)} \end{cases} \Rightarrow \Delta MKO\sim \Delta EAO\Rightarrow\\ \Rightarrow\frac{MK}{OK}=\frac{EA}{OA}=\frac{EA}{1}=EA\\ \Rightarrow EA=\frac{sin\alpha}{cos\alpha}=tg\alpha \end{gather*} Таким образом, построенная вертикальная касательная является числовой прямой, на которой находятся тангенсы.

Ось тангенсов это вертикальная касательная к числовой окружности в точке (1;0), на которой расположены тангенсы соответствующих углов.

Построим горизонтальную касательную к числовой окружности в точке B(0;0).
Продолжим луч OM до пересечения с касательной, обозначим точку пересечения E.
По построению: \begin{gather*} \begin{cases} OK || BE\\ OE - \text{наклонная} \end{cases} \Rightarrow \angle BEO=\angle KOE=\alpha \end{gather*} как накрест лежащие углы. \begin{gather*} \begin{cases} \angle MKO=\angle EBO=90^{\circ}\\ \angle KOM=\angle BEO \end{cases} \Rightarrow \text{(по двум углам)}\\ \Delta MKO\sim \Delta OBE\Rightarrow\\ \Rightarrow\frac{OK}{EB}=\frac{MK}{OB}=\frac{MK}{1}=MK\\ \Rightarrow EB=\frac{OK}{MK}=\frac{cos\alpha}{sin\alpha}=ctg\alpha \end{gather*} Таким образом, построенная горизонтальная касательная является числовой прямой, на которой находятся котангенсы.

Ось котангенсов это горизонтальная касательная к числовой окружности в точке (0;1), на которой расположены котангенсы соответствующих углов.

п.4. Знаки тангенса и котангенса

Знаки синусов и косинусов – см. §2 данного справочника.
Тангенс является отношением синуса к косинусу, поэтому его знаки будут чередоваться при переходе от одной четверти к другой.
Котангенс является тригонометрической функцией, обратной тангенсу, поэтому его знаки будут совпадать со знаками тангенса.

\begin{gather*} tg\alpha\gt 0\ \text{и}\ ctg\alpha\gt 0,\ \ \text{если}\ 0\lt\alpha\lt\frac\pi2\cup\ \pi\lt\alpha\lt\frac{3\pi}{2}\\ tg\alpha\lt 0\ \text{и}\ ctg\alpha\lt 0,\ \ \text{если}\ \frac{\pi}{2}\lt\alpha\lt\pi\cup\ \frac{3\pi}{2}\lt\alpha\lt2\pi \end{gather*}

п.5. Тангенсы и котангенсы углов$\frac{\pi k}{2}$

Синусы и косинусы углов πk/2 – см. §2 данного справочника

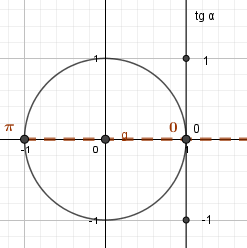Углам 0 и π соответствует 0 на оси тангенсов.	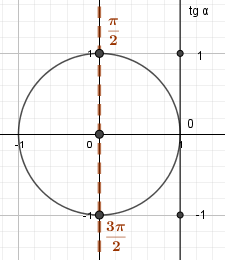Для углов $\frac\pi2$ и $\frac{3\pi}{2}$ проекций на ось тангенсов нет, т.к. соответствующие лучи параллельны и с этой прямой не пересекаются.
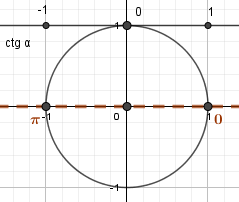Для углов 0 и π проекций на ось котангенсов нет, т.к. соответствующие лучи параллельны и с этой прямой не пересекаются.	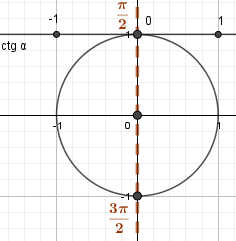Углам $\frac\pi2$ и $\frac{3\pi}{2}$ соответствует 0 на оси котангенсов.

α	0°	90°	180°	270°
α	0	π/2	π	3π/2
tgα	0	+∞	0	–∞
ctgα	+∞	0	–∞	0

п.6. Тангенсы и котангенсы углов $\frac{\pi}{4}+\frac{\pi k}{2}$

Синусы и косинусы углов π/4 + πk/2 – см. §2 данного справочника

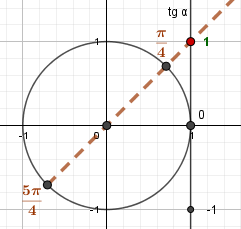Углам $\frac\pi4$ и $\frac{5\pi}{4}$ соответствует 1 на оси тангенсов.	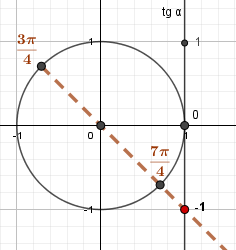Углам $\frac{3\pi}{4}$ и $\frac{7\pi}{4}$ соответствует -1 на оси тангенсов.
Углам $\frac{\pi}{4}$ и $\frac{5\pi}{4}$ соответствует 1 на оси котангенсов.	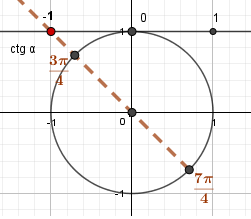Углам $\frac{3\pi}{4}$ и $\frac{7\pi}{4}$ соответствует -1 на оси котангенсов.

α	45°	135°	225°	315°
α	π/4	3π/4	5π/4	7π/4
tgα	1	–1	1	–1
ctgα	1	–1	1	–1

п.7.Тангенсы и котангенсы углов $\frac{\pi}{6}+\frac{\pi k}{2}$

Синусы и косинусы углов π/6 + πk/2 – см. §2 данного справочника

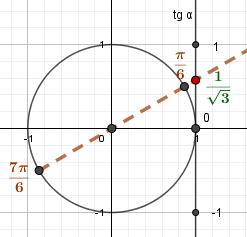Углам $\frac{\pi}{6}$ и $\frac{7\pi}{6}$ соответствует $\frac{1}{\sqrt{3}}$ на оси тангенсов.	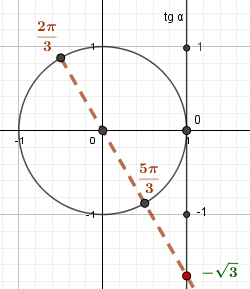Углам $\frac{2\pi}{3}$ и $\frac{5\pi}{3}$ соответствует $-\sqrt{3}$ на оси тангенсов.
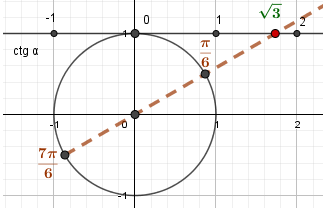Углам $\frac{\pi}{6}$ и $\frac{7\pi}{6}$ соответствует $\sqrt{3}$ на оси котангенсов.	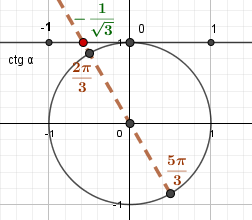Углам $\frac{2\pi}{3}$ и $\frac{5\pi}{3}$ соответствует $\left(-\frac{1}{\sqrt{3}}\right)$ на оси котангенсов.

α	30°	120°	210°	300°
α	π/6	2π/3	7π/6	5π/3
tgα	$\frac{1}{\sqrt{3}}$	$-\sqrt{3}$	$\frac{1}{\sqrt{3}}$	$-\sqrt{3}$
ctgα	$\sqrt{3}$	$-\frac{1}{\sqrt{3}}$	$\sqrt{3}$	$-\frac{1}{\sqrt{3}}$

п.8. Тангенсы и котангенсы углов $\frac{\pi}{3}+\frac{\pi k}{2}$

Синусы и косинусы углов π/3 + πk/2 – см. §2 данного справочника

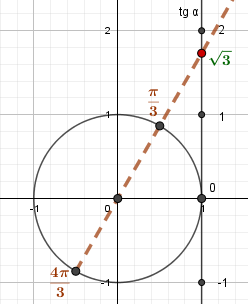Углам $\frac{\pi}{3}$ и $\frac{4\pi}{3}$ соответствует $\sqrt{3}$ на оси тангенсов.	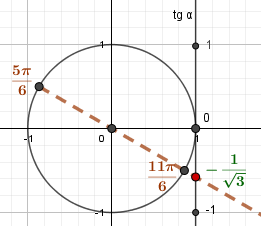Углам $\frac{5\pi}{6}$ и $\frac{11\pi}{6}$ соответствует $\left(-\frac{1}{\sqrt{3}}\right)$ на оси тангенсов.
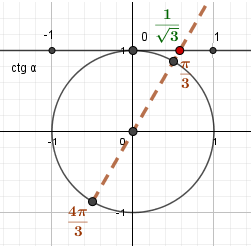Углам $\frac{\pi}{3}$ и $\frac{4\pi}{3}$ соответствует $\frac{1}{\sqrt{3}}$ на оси котангенсов.	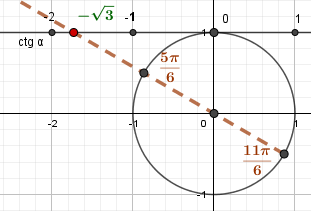Углам $\frac{5\pi}{6}$ и $\frac{11\pi}{6}$ соответствует $\left(-\sqrt{3}\right)$ на оси котангенсов.

α	60°	150°	240°	330°
α	π/3	5π/6	4π/3	11π/6
tgα	$\sqrt{3}$	$-\frac{1}{\sqrt{3}}$	$\sqrt{3}$	$-\frac{1}{\sqrt{3}}$
ctgα	$\frac{1}{\sqrt{3}}$	$-\sqrt{3}$	$\frac{1}{\sqrt{3}}$	$-\sqrt{3}$

п.9. Примеры

Пример 1.
а) Найдите тангенс угла α, если известно, что $sin\alpha=0,8,\ \frac\pi2 \lt \alpha \lt \pi$
Угол находится во второй четверти, значит, косинус отрицательный:
$cos\alpha=-\sqrt{1-sin^2\alpha}=-\sqrt{1-0,8^2}=-\sqrt{0,36}=-0,6$
Тангенс: $tg\alpha=\frac{sin\alpha}{cos\alpha}= \frac{0,8}{-0,6}= - \frac43= - 1\frac13$
б) Найдите котангенс угла, если известно, что $cos\alpha=\frac{5}{13},\ -\frac\pi2 \lt \alpha \lt 0$
Угол находится в четвертой четверти, значит синус отрицательный:
$sin\alpha=-\sqrt{1-cos^2\alpha}=-\sqrt{1-\frac{5}{13}^2}=-\sqrt{\frac{144}{169}}=-\frac{12}{13}$
Котангенс: $ctg\alpha=\frac{cos\alpha}{sin\alpha}=\frac{5}{13}:\left(-\frac{12}{13}\right)=-\frac{5}{12}$

Пример 2. Сравните числа
а) sin20° и tg120°
Угол 20° находится в 1-й четверти, поэтому sin⁡20° > 0
Угол 120° находится в 2-й четверти, поэтому tg120° < 0
Получаем: tg120° < 0 < sin20°
sin⁡20° > tg120°.

б) tg140° и ctg190°
Угол 140° находится во 2-й четверти, поэтому tg140° < 0
Угол 190° находится в 3-й четверти, поэтому ctg190° > 0
Получаем: tg140° < 0 < ctg190°
tg140° < ctg190°.

в) $sin45^{\circ};\ cos135^{\circ};\ tg135^{\circ};\ ctg45^{\circ};\ 0;\ \frac12;\ 2$
$sin45^{\circ}=\frac{\sqrt{2}}{2}\gt \frac12$
$cos135^{\circ}=-\frac{\sqrt{2}}{2}\lt 0$
$tg135^{\circ}=-1\lt-\frac{\sqrt{2}}{2}$
$ctg45^{\circ}=1$
Получаем ряд: $-1\lt-\frac{\sqrt{2}}{2}\lt0\frac12\lt\frac{\sqrt{2}}{2}\lt 2$ $$ tg135^{\circ}\lt cos135^{\circ}\lt 0\lt\frac12\lt sin45^{\circ}\lt ctg45^{\circ}\lt 2 $$

Пример 3. Запишите числа по возрастанию
а) sin60°; cos60°; tg60°; ctg60°; 0; 1; 2
$sin60^{\circ}=\frac{\sqrt{3}}{2}\lt 1$
$cos60^{\circ}=\frac12\lt\frac{\sqrt{3}}{2}$
$tg60^{\circ}=\sqrt{3}\gt 1$
$ctg60^{\circ}=\frac{1}{\sqrt{3}}$
Сравним $\frac{1}{\sqrt{3}}$ и $\frac{\sqrt{3}}{2}$. Для квадратов этих чисел $\frac13\lt\frac34\Rightarrow\frac{1}{\sqrt{3}}\lt\frac{\sqrt{3}}{2}$
Сравним $\frac{1}{\sqrt{3}}$ и $\frac12$. Для квадратов этих чисел $\frac13\gt\frac14\Rightarrow \frac{1}{\sqrt{3}}\gt\frac12$
Получаем ряд: $0\lt \frac12\lt\frac{1}{\sqrt{3}}\lt\frac{\sqrt{3}}{2}\lt 1\lt \sqrt{3}\lt 2$ $$ 0\lt cos60^{\circ}\lt ctg60^{\circ}\lt sin60^{\circ}\lt 1\lt tg60^{\circ}\lt 2 $$
б) sin45°; cos135°; tg135°; ctg45°; 0; $\frac12$; 2
$sin45^{\circ}=\frac{\sqrt{2}}{2}\gt \frac12$
$cos135^{\circ}=-\frac{\sqrt{2}}{2}\lt 0$
$tg135^{\circ}=-1\lt-\frac{\sqrt{2}}{2}$
$ctg45^{\circ}=1$
Получаем ряд: $-1\lt-\frac{\sqrt{2}}{2}\lt 0\lt \frac12\lt\frac{\sqrt{2}}{2}\lt 1\lt 2$ $$ tg135^{\circ}\lt cos135^{\circ}\lt 0\lt\frac12\lt sin45^{\circ}\lt ctg45^{\circ}\lt 2 $$

Рейтинг пользователей

за неделю

за неделю
один месяц
три месяца

Помогай другим

Отвечай на вопросы и получай ценные призы каждую неделю

См. подробности

Углам \(\frac\pi4\) и \(\frac{5\pi}{4}\) соответствует 1 на оси тангенсов.	Углам \(\frac{3\pi}{4}\) и \(\frac{7\pi}{4}\) соответствует -1 на оси тангенсов.
Углам \(\frac{\pi}{4}\) и \(\frac{5\pi}{4}\) соответствует 1 на оси котангенсов.	Углам \(\frac{3\pi}{4}\) и \(\frac{7\pi}{4}\) соответствует -1 на оси котангенсов.

Углам \(\frac{\pi}{6}\) и \(\frac{7\pi}{6}\) соответствует \(\frac{1}{\sqrt{3}}\) на оси тангенсов.	Углам \(\frac{2\pi}{3}\) и \(\frac{5\pi}{3}\) соответствует \(-\sqrt{3}\) на оси тангенсов.
Углам \(\frac{\pi}{6}\) и \(\frac{7\pi}{6}\) соответствует \(\sqrt{3}\) на оси котангенсов.	Углам \(\frac{2\pi}{3}\) и \(\frac{5\pi}{3}\) соответствует \(\left(-\frac{1}{\sqrt{3}}\right)\) на оси котангенсов.

Углам \(\frac{\pi}{3}\) и \(\frac{4\pi}{3}\) соответствует \(\sqrt{3}\) на оси тангенсов.	Углам \(\frac{5\pi}{6}\) и \(\frac{11\pi}{6}\) соответствует \(\left(-\frac{1}{\sqrt{3}}\right)\) на оси тангенсов.
Углам \(\frac{\pi}{3}\) и \(\frac{4\pi}{3}\) соответствует \(\frac{1}{\sqrt{3}}\) на оси котангенсов.	Углам \(\frac{5\pi}{6}\) и \(\frac{11\pi}{6}\) соответствует \(\left(-\sqrt{3}\right)\) на оси котангенсов.

Тангенс и котангенс на единичной числовой окружности

п.1. Тангенс и котангенс острого угла в прямоугольном треугольнике

п.2. Базовые формулы тригонометрии

п.3. Тангенс и котангенс угла на числовой окружности

п.4. Знаки тангенса и котангенса

п.5. Тангенсы и котангенсы углов\(\frac{\pi k}{2}\)

п.6. Тангенсы и котангенсы углов \(\frac{\pi}{4}+\frac{\pi k}{2}\)

п.7.Тангенсы и котангенсы углов \(\frac{\pi}{6}+\frac{\pi k}{2}\)

п.8. Тангенсы и котангенсы углов \(\frac{\pi}{3}+\frac{\pi k}{2}\)

п.9. Примеры

Рейтинг пользователей

Углам 0 и π соответствует 0 на оси тангенсов.	Для углов \(\frac\pi2\) и \(\frac{3\pi}{2}\) проекций на ось тангенсов нет, т.к. соответствующие лучи параллельны и с этой прямой не пересекаются.
Для углов 0 и π проекций на ось котангенсов нет, т.к. соответствующие лучи параллельны и с этой прямой не пересекаются.	Углам \(\frac\pi2\) и \(\frac{3\pi}{2}\) соответствует 0 на оси котангенсов.