Синус и косинус на единичной числовой окружности
- Синус и косинус острого угла в прямоугольном треугольнике
- Основное тригонометрическое тождество
- Синус и косинус угла на числовой окружности
- Знаки синусов и косинусов
- Синусы и косинусы углов πk/2
- Синусы и косинусы углов π/4+πk/2
- Синусы и косинусы углов π/6+πk/2
- Синусы и косинусы углов π/3+πk/2
- Примеры
п.1. Синус и косинус острого угла в прямоугольном треугольнике
 |
Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе. sinα=$\frac{a}{c} $ Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе. cosα=$\frac{b}{c} $ |
B ΔABC, ∠C = 90°, a = 2, b = 4. Найдем синус и косинус ∠A.
По теореме Пифагора гипотенуза равна \(c=\sqrt{a^2+b^2}=\sqrt{2^2+4^2}=2\sqrt{5}\)
Получаем: $$ sinA=\frac{a}{c}=\frac{2}{2\sqrt{5}}=\frac{1}{\sqrt{5}},\ \ cosA=\frac{b}{c}=\frac{4}{2\sqrt{5}}=\frac{2}{\sqrt{5}} $$
п.2. Основное тригонометрическое тождество
Из теоремы Пифагора следует: $$ a^2+b^2=c^2\Rightarrow \frac{a^2+b^2}{c^2}=1\Rightarrow\left(\frac{a}{c}\right)^2+\left(\frac{b}{c}\right)^2=1\Rightarrow sin^2\alpha+cos^2\alpha=1 $$
п.3. Синус и косинус угла на числовой окружности
 |
Числовая окружность расположена в декартовой прямоугольной системе координат. Отметим на числовой окружности точку M, где луч OM составляет с положительным направлением оси OX угол α. Найдем координаты точки M. Рассмотрим ΔMOK. ∠MKO=90°, ∠MOK=α OM=1 – гипотенуза По определению синуса и косинуса острого угла в прямоугольном треугольнике получаем: \begin{gather*} cos\alpha=\frac{OK}{OM}=\frac{x}{1}=x\\ sin\alpha=\frac{MK}{OM}=\frac{y}{1}=y \end{gather*} |
Уравнение числовой окружности по определению: x2 + y2 = 1
Откуда снова получаем основное тригонометрическое тождество:
п.4. Знаки синусов и косинусов
| Знак косинуса - это знак координаты x для точки на числовой окружности | Знак синуса - это знак координаты y для точки на числовой окружности |
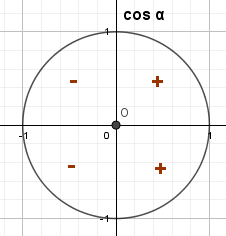 |
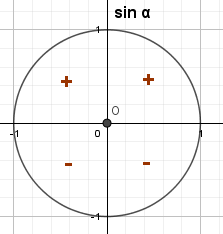 |
| \begin{gather*} cos\alpha\gt 0,\ \ \text{если}\ -\frac{\pi}{2}\lt\alpha \lt \frac{\pi}{2}\\ cos\alpha\lt 0,\ \ \text{если}\ \frac{\pi}{2}\lt\alpha\lt \frac{3\pi}{2} \end{gather*} | \begin{gather*} sin\alpha\gt 0,\ \ \text{если}\ 0\lt \alpha \lt \pi\\ sin\alpha\lt 0,\ \ \text{если}\ \pi\lt \alpha \lt 2\pi \end{gather*} |
п.5. Синусы и косинусы углов \(\frac{\pi k}{2}\)
 |
Базовыми точками на числовой окружности для углов, кратных прямому углу (углы \(\frac{\pi k}{2}\)), будут четыре точки: 0°, 90°, 180°, 270° \(\left(0,\ \frac{\pi}{2},\ \pi,\ \frac{3\pi}{2}\right)\). Все остальные точки (например, 360°, 900° или –540°) будут отличаться от базовых точек на один или несколько полных периодов 2πk, т.е. будут совпадать с ними на окружности. Синусы и косинусы для совпадающих точек равны. Косинус – это координата x, синус – координата y. |
| α | 0° | 90° | 180° | 270° | |
| 0 | π/2 | π | 3π/2 | ||
| x | cosα | 1 | 0 | –1 | 0 |
| y | sinα | 0 | 1 | 0 | –1 |
п.6. Синусы и косинусы углов \(\frac{\pi}{4}+\frac{\pi k}{2}\)
 |
Базовыми точками на числовой окружности для угла 45° и всех отстоящих от него на углы, кратные прямому (углы \(\frac{\pi}{4}+\frac{\pi k}{2}\)), будут четыре точки: 45°, 135°, 225°, 315° \(\left(\frac{\pi}{4},\ \frac{3\pi}{4},\ \frac{5\pi}{4},\ \frac{7\pi}{4}\right)\). Все остальные точки (например, 405°, 945° или –585°) будут отличаться от базовых точек на один или несколько полных периодов 2πk, т.е. будут совпадать с ними на окружности. Синусы и косинусы для совпадающих точек равны. Косинус – это координата x, синус – координата y. |
Как видно из чертежа, для этих углов синус и косинус по модулю равны и отличаются только по знаку. Найдем модуль из тригонометрического тождества.
Обозначим для угла \(45^{\circ} sin45^{\circ}=cos45^{\circ}=m\gt 0.\) Тогда
$$ sin^2 45^{\circ}+cos^2 45^{\circ}=1\Rightarrow m^2+m^2=1\Rightarrow 2m^2=1\Rightarrow m^2=\frac12 \overset{m\gt 0}{\Rightarrow} m=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2} $$ Все исследуемые точки на числовой окружности будут иметь пару координат \(\frac{\sqrt{2}}{2}\ \text{и}\ \frac{\sqrt{2}}{2}\), только с разными знаками.
| α | 45° | 135° | 225° | 315° | |
| π/4 | 3π/4 | 5π/4 | 7π/4 | ||
| x | cosα | \(\frac{\sqrt{2}}{2}\) | \(-\frac{\sqrt{2}}{2}\) | \(-\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{2}}{2}\) |
| y | sinα | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(-\frac{\sqrt{2}}{2}\) | \(-\frac{\sqrt{2}}{2}\) |
п.7. Синусы и косинусы углов π/6+πk/2
 |
Базовыми точками на числовой окружности для угла 30° и всех отстоящих от него на углы, кратные прямому (углы \(\frac{\pi}{6}+\frac{\pi k}{2}\)), будут четыре точки: 30°, 120°, 210°, 300° \(\left(\frac{\pi}{6},\ \frac{2\pi}{3},\ \frac{7\pi}{6},\ \frac{5\pi}{3}\right)\). Все остальные точки (например, 390°, 960° или –420°) будут отличаться от базовых точек на один или несколько полных периодов 2πk, т.е. будут совпадать с ними на окружности. Синусы и косинусы для совпадающих точек равны. Косинус – это координата x, синус – координата y. |
Известно, что \(sin 30^{\circ}=\frac12\). Тогда из основного тригонометрического тождества: $$ cos30^{\circ}=\sqrt{1-sin^230^{\circ}}=\sqrt{1-\frac14}=\frac{\sqrt{3}}{2}. $$ Все исследуемые точки на числовой окружности будут иметь пару координат из чисел \(\frac12\ \text{и}\ \frac{\sqrt{3}}{2}\) в разном порядке и с разными знаками. Чтобы различать их «на глаз», заметим, что \(\frac{\sqrt{3}}{2}\approx 0,87\gt\frac12\). Т.е, отрезок короче будет равен по модулю \(\frac12\), а длиннее \(\frac{\sqrt{3}}{2}\).
| α | 30° | 120° | 210° | 300° | |
| π/6 | 2π/3 | 7π/6 | 5π/3 | ||
| x | cosα | \(\frac{\sqrt{3}}{2}\) | \(-\frac12\) | \(-\frac{\sqrt{3}}{2}\) | \(\frac12\) |
| y | sinα | \(\frac12\) | \(\frac{\sqrt{3}}{2}\) | \(-\frac12\) | \(-\frac{\sqrt{3}}{2}\) |
п.8. Синусы и косинусы углов π/3+πk/2
 |
Базовыми точками на числовой окружности для угла 60° и всех отстоящих от него на углы, кратные прямому (углы \(\frac{\pi}{3}+\frac{\pi k}{2}\)), будут четыре точки: 60°, 150°, 240°, 330° \(\left(\frac{\pi}{3},\ \frac{5\pi}{6},\ \frac{4\pi}{3},\ \frac{11\pi}{6}\right)\). Все остальные точки (например, 390°, 960° или –420°) будут отличаться от базовых точек на один или несколько полных периодов 2πk, т.е. будут совпадать с ними на окружности. Синусы и косинусы для совпадающих точек равны. Косинус – это координата x, синус – координата y. |
Известно, что \(cos60^{\circ}=sin 30^{\circ}=\frac12\). Тогда из основного тригонометрического тождества: $$ sin60^{\circ}=\sqrt{1-cos^2 60^{\circ}}=\sqrt{1-\frac14}=\frac{\sqrt{3}}{2}. $$ Все исследуемые точки на числовой окружности будут иметь пару координат из чисел \(\frac12\ \text{и}\ \frac{\sqrt{3}}{2}\) в разном порядке и с разными знаками. Чтобы различать их «на глаз», заметим, что \(\frac{\sqrt{3}}{2}\approx 0,87\gt\frac12\). Т.е, отрезок короче будет равен по модулю \(\frac12\), а длиннее \(\frac{\sqrt{3}}{2}\).
| α | 60° | 150° | 240° | 330° | |
| π/3 | 5π/6 | 4π/3 | 11π/6 | ||
| x | cosα | \(\frac12\) | \(-\frac{\sqrt{3}}{2}\) | \(-\frac12\) | \(\frac{\sqrt{3}}{2}\) |
| y | sinα | \(\frac{\sqrt{3}}{2}\) | \(\frac12\) | \(-\frac{\sqrt{3}}{2}\) | \(-\frac12\) |
п.9. Примеры
Пример 1.
а) Найдите косинус угла α, если известно, что \(sin\alpha=0,8,\ \frac\pi2 \lt \alpha \lt \pi\)
Угол находится во второй четверти, значит, косинус отрицательный:
\(cos\alpha=-\sqrt{1-sin^2\alpha}=-\sqrt{1-0,8^2}=-\sqrt{0,36}=-0,6\)
б) Найдите синус угла, если известно, что \(cos\alpha=\frac{5}{13},\ -\frac\pi2 \lt \alpha \lt 0\)
Угол находится в четвертой четверти, значит синус отрицательный:
\(sin\alpha=-\sqrt{1-cos^2\alpha}=-\sqrt{1-\frac{5}{13}^2}=-\sqrt{\frac{144}{169}}=-\frac{12}{13}\)
Пример 2. Сравните числа
а) sin10° и sin320°
Угол 10° находится в 1-й четверти, sin10° > 0
Угол 320° находится в 4-й четверти, sin320° < 0
Получаем: sin320° < 0 < sin10°
sin10° > sin320°.
б) cos115° и sin85°
Угол 85° находится в 1-й четверти, sin85° > 0
Угол 115° находится во 2-й четверти, cos115° < 0
Получаем: cos115° < 0 < sin85°
cos115° < sin85°.
в) \(sin\frac{8\pi}{7}\) и \(cos\frac{11\pi}{25}\)
\(\pi\lt \frac{8\pi}{7}\lt \frac{3\pi}{2}\Rightarrow\) угол \(\frac{8\pi}{7}\) находится в 3-й четверти, \(sin\frac{8\pi}{7}\lt 0\)
\(0\lt \frac{11\pi}{25}\lt \frac{\pi}{2}\Rightarrow\) угол \(\frac{11\pi}{25}\) находится в 1-й четверти, \(cos\frac{11\pi}{25}\gt 0\)
Получаем: \(sin\frac{8\pi}{7} \lt 0\lt cos\frac{11\pi}{25}\)
\(sin\frac{8\pi}{7}\lt cos\frac{11\pi}{25}\)
Пример 3. Заданы точки на числовой окружности. Найдите их координаты
\begin{gather*} a)\ M\left(\frac{5\pi}{6}\right)\\ \frac{5\pi}{6}=5\cdot \frac\pi6=5\cdot30^{\circ}=150^{\circ} \end{gather*}  Косинус – длинный отрицательный \((-\frac{\sqrt{3}}{2})\) Синус – короткий положительный \(\left(\frac12\right)\) \begin{gather*} x=cos\frac{5\pi}{6}=-\frac{\sqrt{3}}{2}\\ y=sin\frac{5\pi}{6}=\frac12 \end{gather*} |
\begin{gather*} б)\ M\left(-\frac{2\pi}{3}\right)\\ -\frac{2\pi}{3}=-2\cdot \frac\pi3=-2\cdot 60^{\circ}=-120^{\circ} \end{gather*} 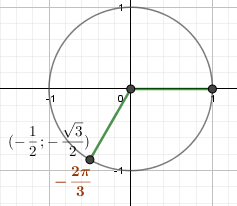 Косинус – короткий отрицательный \(\left(-\frac12\right)\) Синус – длинный отрицательный \((-\frac{\sqrt{3}}{2})\) \begin{gather*} x=cos\left(-\frac{2\pi}{3}\right)=-\frac12\\ y=sin\left(-\frac{2\pi}{3}\right)=-\frac{\sqrt{3}}{2} \end{gather*} |
\begin{gather*} в)\ M\left(\frac{5\pi}{2}\right)\\ \frac{5\pi}{2}=\left(2+\frac12\right)\pi=2\pi+\frac\pi2\rightarrow\frac\pi2=90^{\circ} \end{gather*} 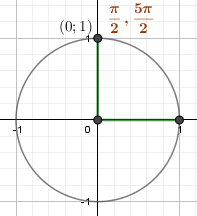 \begin{gather*} x=cos\frac{5\pi}{2}=cos\frac\pi2=0\\ y=sin\frac{5\pi}{2}=sin\frac\pi2=1 \end{gather*} \begin{gather*} x=cos\frac{5\pi}{2}=cos\frac\pi2=0\\ y=sin\frac{5\pi}{2}=sin\frac\pi2=1 \end{gather*} |
\begin{gather*} г)\ M\left(-\frac{16\pi}{3}\right)\\ -\frac{16\pi}{3}=\frac{-18+2}{3}\pi=-6\pi+\frac{2\pi}{3}\rightarrow\frac{2\pi}{3}= 120^{\circ} \end{gather*} 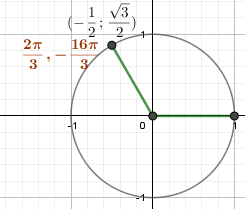 Косинус – короткий отрицательный \(\left(-\frac12\right)\) Синус – длинный положительный \(\left(\frac{\sqrt{3}}{2}\right)\) \begin{gather*} x=cos\left(-\frac{16\pi}{3}\right)=cos\frac{2\pi}{3}=-\frac12\\ y=sin\left(-\frac{16\pi}{3}\right)=sin\frac{2\pi}{3}=\frac{\sqrt{3}}{2} \end{gather*} |
Пример 4. Найти sint,cost для данных t.
\(a)\ t=\frac{13\pi}{4}\)
 |
Отнимем полный оборот: \(\frac{13\pi}{4}-2\pi=\frac{13-8}{4}\pi=\frac{5\pi}{4}\) Угол кратный \(\frac\pi4\), его синус и косинус по модулю равны \(\frac{\sqrt{2}}{2}\), знаки определяются расположением угла. \(\pi\lt\frac{5\pi}{4}\lt\frac{3\pi}{2}\Rightarrow\) угол находится в 3-й четверти, синус и косинус отрицательные. Получаем: \begin{gather*} sin\frac{13\pi}{4}=sin\frac{5\pi}{4}=-\frac{\sqrt{2}}{2}\\ cos\frac{13\pi}{4}=cos\frac{5\pi}{4}=-\frac{\sqrt{2}}{2} \end{gather*} |
\(б)\ t=\frac{11\pi}{2}\)
 |
Отнимем 2 полных оборота: \(\frac{11\pi}{2}-2\cdot 2\pi=\frac{11-8}{2}\pi=\frac{3\pi}{2}\) Угол кратный \(\frac\pi2\), находится на оси Y, в нижней точке числовой окружности. Получаем: \begin{gather*} sin\frac{11\pi}{2}=sin\frac{3\pi}{2}=-1\\ cos\frac{11\pi}{2}=cos\frac{3\pi}{2}=0 \end{gather*} |
\(в)\ t=\frac{17\pi}{6}\)
 |
Отнимем полный оборот: \(\frac{17\pi}{6}-2\pi=\frac{17-12}{6}\pi=\frac{5\pi}{6}\) Угол типа \(\frac\pi6\), в котором синус и косинус – это пара из \(\frac12\) и \(\frac{\sqrt{3}}{2}\), фактическое значение определяется по чертежу, исходя из того, что \(\frac{\sqrt{3}}{2}\approx 0,87\gt\frac12\). Знаки определяются по расположению угла в четверти: \(\frac\pi2\lt\frac{5\pi}{6}\lt\pi\Rightarrow\) угол находится во 2-й четверти. Из чертежа получаем: Косинус – длинный отрицательный Синус – короткий положительный Таким образом: \begin{gather*} sin\frac{17\pi}{6}=sin\frac{5\pi}{6}=\frac12\\ cos\frac{17\pi}{6}=cos\frac{5\pi}{6}=-\frac{\sqrt{3}}{2} \end{gather*} |
\(г)\ t=-\frac{4\pi}{3}\)
 |
Добавим полный оборот: \(-\frac{4\pi}{3}+2\pi=\frac{-4+6}{3}\pi=\frac{2\pi}{3}\) Угол типа \(\frac\pi3\), в котором синус и косинус – это пара из \(\frac12\) и \(\frac{\sqrt{3}}{2}\), фактическое значение определяется по чертежу, исходя из того, что \(\frac{\sqrt{3}}{2}\approx 0,87\gt\frac12\). Знаки определяются по расположению угла в четверти: \(\frac\pi2\lt\frac{2\pi}{3}\lt\pi\Rightarrow\) угол находится во 2-й четверти. Из чертежа получаем: Косинус – короткий отрицательный Синус – длинный положительный Таким образом: \begin{gather*} sin\left(-\frac{4\pi}{3}\right)=sin\frac{2\pi}{3}=\frac{\sqrt{3}}{2}\\ cos\left(-\frac{4\pi}{3}\right)=cos\frac{2\pi}{3}=-\frac12 \end{gather*} |


