Решение тригонометрических неравенств и систем

п.1. Примеры

Пример 1. Решите неравенства:
a) \(ctg\left(\frac{3\pi}{2}+\frac x3\right)-\frac{1}{\sqrt{3}}\leq 0\)
По формуле приведения \(ctg\left(\frac{3\pi}{2}+\frac x3\right)=-tg\frac x3\)
Получаем:
\(-tg\frac x3-\frac{1}{\sqrt{3}}\leq 0\Rightarrow tg\frac x3\geq \frac{1}{\sqrt{3}}\)
\(arctg\frac{1}{\sqrt{3}}+\pi k\leq\frac x3\lt\frac\pi2+\pi k\)
\(3\cdot\frac\pi6+3\pi k\leq x\lt\frac{3\pi}{2}+3\pi k\)
\(\frac\pi2+3\pi k\leq x\lt\frac{3\pi}{2}+3\pi k\)

Ответ: \(\left.\left[\frac\pi2+3\pi k;\ \frac{3\pi}{2}+3\pi k\right.\right) \)

б) \(tg\left(2x+\frac\pi4\right)+1\geq 0\)
\(tg\left(2x+\frac\pi4\right)\geq -1\)
\(-\frac\pi4+\pi k\leq 2x+\frac\pi4\lt\frac\pi2+\pi k\)
\(-\frac\pi2+\pi k\leq 2x\lt\frac\pi4+\pi k\)
\(-\frac\pi4+\frac{\pi k}{2}\leq x\lt\frac\pi8+\frac{\pi k}{2}\)
Ответ: \(\left.\left[-\frac\pi4+\frac{\pi k}{2};\ \frac\pi8+\frac{\pi k}{2}\right.\right) \)

в) \(3cos2x\leq 1\) \begin{gather*} cos2x\leq\frac13\\ arccos\frac13+2\pi k\leq 2x\leq 2\pi-arccos\frac13+2\pi k\\ \frac12 arccos\frac13+\pi k\leq x\leq \pi-\frac12 arccos\frac13+\pi k \end{gather*} Ответ: \(\left[ \frac12 arccos\frac13+\pi k;\ \pi-\frac12 arccos\frac13+\pi k\right] \)

г) \(cos^2x-2cosx\gt 0\)
\(cosx(cosx-2)\gt 0\)
\(cosx-2\lt 0\) при любом \(x\). Делим неравенство на отрицательную скобку, получаем:
\(cosx\lt 0\)
\(\frac\pi2+2\pi k\lt x\lt\frac{3\pi}{2}+2\pi k\)
Ответ: \(\left(\frac\pi2+2\pi k;\ \frac{3\pi}{2}+2\pi k\right) \)

Пример 2*. Решите неравенства:

a) \(\frac12\lt sinx\leq \frac{\sqrt{2}}{2}\) Ответ: $$ \left.\left(\frac\pi6+2\pi k;\ \frac\pi4+2\pi k\right.\right]\cup \left.\left[\frac{3\pi}{4}+2\pi k;\ \frac{5\pi}{6}+2\pi k\right.\right) $$

б) \(sin2x+\sqrt{3}cos2x\geq 1\) Вводим вспомогательный угол, умножаем на \(\frac12\) \begin{gather*} \frac12 sin2x+\frac{\sqrt{3}}{2}cos2x\geq\frac12\\ sin\frac\pi6 sin2x+cos\frac\pi6 cos2x\geq\frac12\\ cos\left(2x-\frac\pi6\right)\geq\frac12\\ -\frac{\pi}{3}+2\pi k\leq 2x-\frac\pi6\leq \frac\pi3+2\pi k\\ -\frac\pi6+2\pi k\leq 2x\leq \frac\pi2+2\pi k\\ -\frac{\pi}{12}+\pi k\leq x \leq \frac\pi4+\pi k \end{gather*} Ответ: $$ \left[-\frac{\pi}{12}+\pi k;\ \frac\pi4+\pi k\right] $$

в) \(tg^2x-\left(1+\sqrt{3}\right)tg x+\sqrt{3}\lt 0\)
\(tg^2x-tgx-\sqrt{3}tgx+\sqrt{3}\lt 0\)
\(tgx(tgx-1)-\sqrt{3}(tgx-1)\lt 0\)
\((tgx-\sqrt{3})(tgx-1)\lt 0\)
\(1\lt tgx\lt \sqrt{3}\)
\(arctg1+\pi k\lt x\lt arctg\sqrt{3}+\pi k\)
\(\frac\pi4+\pi k\lt x\lt\frac\pi6+\pi k\)
Ответ: \(\left(\frac\pi4+\pi k;\ \frac\pi6+\pi k\right)\)

г) \(\sqrt{5-2sinx}\geq 6sinx-1\)
Замена: \(t=sinx,\ -1\leq t\leq 1\)
Методы решения иррациональных неравенств – см. §11 справочника для 9 класса. \begin{gather*} \begin{cases} \sqrt{5-2t}\geq 6t-1\\ -1\leq t\leq 1 \end{cases} \Rightarrow \begin{cases} \left[ \begin{array}{l l} \begin{cases} 6t-1\lt 0\\ 5-2t\geq 0 \end{cases} \\ \begin{cases} 6t-1\geq 0\\ 5-2t\geq (6t-1)^2 \end{cases} \end{array} \right. \\ -1\leq t\leq 1 \end{cases} \Rightarrow \begin{cases} \left[ \begin{array}{l l} \begin{cases} t\lt\frac16\\ t\leq\frac52 \end{cases} \\ \begin{cases} t\geq\frac16\\ 5-2t\geq 36t^2-12t+1 \end{cases} \end{array} \right. \\ -1\leq t\leq 1 \end{cases} \Rightarrow \\ \Rightarrow \begin{cases} \left[ \begin{array}{l l} t\lt\frac16 \\ \begin{cases} t\geq\frac16\\ 18t^2-5t-2\leq 0 \end{cases} \end{array} \right. \\ -1\leq t\leq 1 \end{cases} \Rightarrow \begin{cases} \left[ \begin{array}{l l} t\lt\frac16 \\ \begin{cases} t\geq\frac16\\ (9t+2)(2t-1)\leq 0 \end{cases} \end{array} \right. \\ -1\leq t\leq 1 \end{cases} \Rightarrow \begin{cases} \left[ \begin{array}{l l} t\lt\frac16 \\ \begin{cases} t\geq\frac16\\ -\frac29\leq t\leq \frac12 \end{cases} \end{array} \right. \\ -1\leq t\leq 1 \end{cases} \Rightarrow \\ \Rightarrow \begin{cases} \left[ \begin{array}{l l} t\lt\frac16 \\ \frac16\leq t\leq\frac12 \end{array} \right. \\ -1\leq t\leq 1 \end{cases} \Rightarrow \begin{cases} t\leq\frac12 \\ -1\leq t\leq 1 \end{cases} \Rightarrow -1\leq t\leq\frac12 \end{gather*} Возвращаемся к исходной переменной: $$ -1\leq sinx\leq\frac12 \Rightarrow sinx\leq\frac12\Rightarrow -\frac{7\pi}{6}+2\pi k\leq x\leq \frac\pi6+2\pi k $$
Ответ: \(\left[-\frac{7\pi}{6}+2\pi k;\ \frac\pi6+2\pi k\right]\)

Пример 3*. Решите системы:
a) \begin{gather*} \begin{cases} sin^2x+sin^2x=sin^2 3x\\ cosx\lt-\frac12 \end{cases} \end{gather*} Решаем уравнение: \begin{gather*} sin^2 2x=sin^2 3x-sin^2x=(sin3x+sinx)(sin3x-sinx)\\ sin^22x=2sin2xcosx\cdot 2sinxcos2x=sin2x\cdot(2sinxcosx)\cdot 2cos2x\\ sin^22x=sin^22x\cdot 2cos2x\\ sin^22x(1-2cos2x)=0\\ \left[ \begin{array}{l l} sin^22x=0\\ 1-2cos2x=0 \end{array} \right. \Rightarrow \left[ \begin{array}{l l} \frac{1-cos4x}{2}=0\\ cos2x=\frac12 \end{array} \right. \Rightarrow \left[ \begin{array}{l l} cos4x=1\\ 2x=\pm\frac\pi3+2\pi k \end{array} \right. \Rightarrow \left[ \begin{array}{l l} 4x=2\pi k\\ x=\pm\frac\pi6+\pi k \end{array} \right. \Rightarrow\\ \Rightarrow \left[ \begin{array}{l l} x=\frac{\pi k}{2} \\ x=\pm\frac\pi6+\pi k \end{array} \right. \end{gather*}

Отмечаем полученные решения на числовой окружности, задаем дугу \(cosx\lt-\frac12\), отбираем решения, попавшие на дугу. Получаем три базовых точки \(\pm\frac{5\pi}{6},\pi\). С учетом полного периода 2πk записываем всё множество решений.

Ответ: \(\left\{\pm\frac{5\pi}{6}+2\pi k,\ \pi+2\pi k\right\}\)

б) \begin{gather*} \begin{cases} 2sin^2x-sinx+sin3x\lt 1\\ cosx\gt 0 \end{cases} \end{gather*} Разность синусов: \(sin⁡3x-sin⁡x=2sin⁡xcos⁡2x\)
В первом неравенстве получаем: \begin{gather*} 2sin^2x+2sinxcos2x\lt 1\\ 2sinxcos2x\lt 1-2sin^2x\\ 2sinxcos2x\lt cos2x\\ cos2x(2sinx-1)\lt 1\\ \left[ \begin{array}{l l} \begin{cases} cos2x\gt 0\\ 2sinx-1\lt 0 \end{cases} \\ \begin{cases} cos2x\lt 0\\ 2sinx-1\gt 0 \end{cases} \end{array} \right. \Rightarrow \left[ \begin{array}{l l} \begin{cases} -\frac\pi2+2\pi k\lt 2x\lt\frac\pi2+2\pi k\\ sinx\lt\frac12 \end{cases} \\ \begin{cases} \frac\pi2+2\pi k\lt 2x\lt\frac{3\pi}{2}+2\pi k\\ sinx\gt\frac12 \end{cases} \end{array} \right. \Rightarrow \left[ \begin{array}{l l} \begin{cases} -\frac\pi4+\pi k\lt x\lt\frac\pi4+\pi k\\ sinx\lt\frac12 \end{cases} \\ \begin{cases} \frac\pi4+\pi k\lt x\lt\frac{3\pi}{4}+\pi k\\ sinx\gt\frac12 \end{cases} \end{array} \right. \end{gather*}

$$ \begin{cases} \frac\pi4+\pi k\lt x\lt\frac{\pi}{4}+\pi k\\ sinx\lt\frac12 \end{cases} $$ 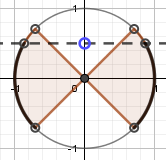$$ \left(-\frac\pi4;\ \frac\pi6\right)\cup \left(\frac{5\pi}{6};\ \frac{5\pi}{4}\right) $$ С полным периодом \(2\pi k\)

$$ \begin{cases} \frac\pi4+\pi k\lt x\lt\frac{3\pi}{4}+\pi k\\ sinx\gt\frac12 \end{cases} $$ $$ \left(\frac\pi4;\ \frac{3\pi}{4}\right) $$ С полным периодом \(2\pi k\)

Учитываем второе неравенство, \(cosx\gt 0\). Отбираем только решения справа от оси \(Y\).
Получаем: \(\left(-\frac\pi4;\frac\pi6\right)\cup\left(\frac\pi4;\frac\pi2\right)\)
Ответ: \(\left(-\frac\pi4+2\pi k;\ \frac\pi6+2\pi k\right)\cup \left(\frac\pi4+2\pi k;\ \frac\pi2+2\pi k\right)\)