Проверка статистических гипотез
п.1. Понятие о статистической гипотезе
Прежде всего, мы формулируем «рабочую» гипотезу. Желательно это делать не на основе полученных данных, а исходя из природы и свойств исследуемого явления.
Затем формулируется нулевая гипотеза \(H_0\), отвергающая нашу рабочую гипотезу.
Наша рабочая гипотеза при этом называется альтернативной гипотезой \(H_1\).
Получаем, что \(H_0=\overline{H_1}\), т.е. нулевая и альтернативная гипотеза вместе составляют полную группу несовместных событий.
В результате проверки гипотезы возможны 4 исхода:
| Верная гипотеза | |||
| \(H_0\) | \(H_1\) | ||
| Принятая гипотеза | \(H_0\) | True Negative \(H_0\) принята верно |
False Negative \(H_0\) принята неверно Ошибка 2-го рода |
| \(H_1\) | False Positive \(H_0\) отвергнута неверно \(H_1\) принята неверно Ошибка 1-го рода |
True Positive \(H_0\) отвергнута верно \(H_1\) принята верно |
|
Ошибка 1-го рода – «ложная тревога».
Ошибка 2-го рода – «пропуск события».
Например:
К врачу обращается человек с некоторой жалобой.
Гипотеза \(H_1\) - человек болен, гипотеза \(H_0\) - человек здоров.
True Negative – здорового человека признают здоровым
True Positive – больного человека признают больным
False Positive – здорового человека признают больным – «ложная тревога»
False Negative – больного человека признают здоровым – «пропуск события»
Уровень значимости при проверке гипотезы
В статистике разработано множество критериев: критерии согласия, критерии нормальности, критерии сдвига, критерии выбросов и т.д.
Требуемый уровень значимости α задает критическое значение для статистического теста.
Например:
Уровень значимости α=0,05 означает, что допускается не более чем 5%-ая вероятность ошибки.
Обобщив практический опыт, можно сформулировать следующие рекомендации для оценки p и выбора критического значения α:
| Уровень значимости \(p\) |
Решение о гипотезе \(H_0\) | Вывод для гипотезы \(H_1\) |
| \(p\gt 0,1\) | \(H_0\) не может быть отклонена | Статистически достоверные доказательства не обнаружены |
| \(0,5\lt p\leq 0,1\) | Истинность \(H_0\) сомнительна, неопределенность | Доказательства обнаружены на уровне статистической тенденции |
| \(0,01\lt p\leq 0,05\) | Отклонение \(H_0\), значимость | Обнаружены статистически достоверные (значимые) доказательства |
| \(p\leq 0,01\) | Отклонение \(H_0\), высокая значимость | Доказательства обнаружены на высоком уровне значимости |
Здесь под «доказательствами» мы понимаем результаты наблюдений, свидетельствующие в пользу гипотезы \(H_1\).
Традиционно уровень значимости α=0,05 выбирается для небольших выборок, в которых велика вероятность ошибки 2-го рода. Для выборок с \(n\geq 100\) критический уровень снижают до α=0,01.
п.3. Критическая область
Требуемый уровень значимости α, который задается исследователем, определяет границу попадания в критическую область при верной нулевой гипотезе.
Различают 3 вида критических областей
Двусторонняя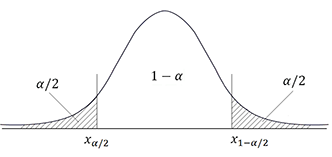 $$ \left(-\infty;\chi_{\alpha/2}\right)\cup\left(\chi_{1-\alpha/2};+\infty\right) $$ |
||
Левосторонняя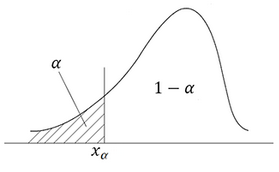 $$ \left(-\infty;\chi_{\alpha}\right) $$ |
Правосторонняя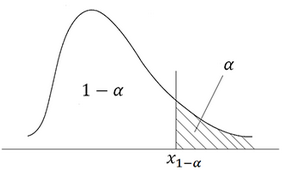 $$ \left(\chi_{1-\alpha};+\infty\right) $$ |
|
Критическая область на чертежах заштрихована.
\(K_{кр}=\chi_{f(\alpha)}\) определяют границы критической области в зависимости от α.
Если эмпирическое значение критерия попадает в критическую область, гипотезу \(H_0\) отклоняют.
Пусть \(K*\) - эмпирическое значение критерия. Тогда:
\(|K|\gt K_{кр}\) – гипотеза \(H_0\) отклоняется
\(|K|\leq K_{кр}\) – гипотеза \(H_0\) не отклоняется
п.4. Простая гипотеза и критерии согласия
Простая гипотеза состоит в предположении, что неизвестная функция \(F(t)\) является совершенно конкретным вероятностным распределением на множестве \(X\).
Например: 
Глядя на полученные данные эксперимента (синие точки), можно выдвинуть следующую простую гипотезу:
\(H_0\): данные являются выборкой из равномерного распределения на отрезке [-1;1]
К критериям согласия относятся:
- Критерий Колмогорова-Смирнова;
- Критерий \(X^2\) Пирсона;
- Критерий \(\omega^2\) Смирнова-Крамера-фон Мизеса
п.5. Критерий согласия \(X^2\) Пирсона
Пусть \(\left\{t_1,t_2,…,t_n\right\}\) - независимые случайные величины, подчиняющиеся стандартному нормальному распределению N(0;1) (см. §63 данного справочника)
Тогда сумма квадратов этих величин: $$ x=t_1^2+t_2^2+⋯+t_n^2 $$ является случайной величиной, которая имеет распределение \(X^2\) с n степенями свободы.
График плотности распределения \(X^2\) при разных n имеет вид: 
С увеличением n распределение \(X^2\) стремится к нормальному (согласно центральной предельной теореме – см. §64 данного справочника).
Если мы:
1) выдвигаем простую гипотезу \(H_0\) о том, что полученные данные являются выборкой из некоторого закона распределения \(f(x)\);
2) выбираем в качестве теста проверки гипотезы \(H_0\) критерий Пирсона, -
тогда определение критической области будет основано на распределении \(X^2\).
Заметим, что выдвижение основной гипотезы в качестве \(H_0\) при проведении этого теста исторически сложилось.
В этом случае критическая область правосторонняя.
Мы задаем уровень значимости α и находим критическое значение
\(X_{кр}^2=X^2(\alpha,k-r-1)\), где k - число вариант в исследуемом ряду, r – число параметров предполагаемого распределения.
Для этого есть специальные таблицы.
Или используем функцию ХИ2ОБР(α,k-r-1) в MS Excel (она сразу считает нужный нам правый хвост). Например, при r=0 (для равномерного распределения):
Пусть нам дан вариационный ряд с экспериментальными частотами \(f_i,\ i=\overline{1,k}\).
Пусть наша гипотеза \(H_0\) –данные являются выборкой из закона распределения с известной плотностью распределения \(p(x)\).
Тогда соответствующие «теоретические частоты» \(m_i=Ap(x_i)\), где \(x_i\) – значения вариант данного ряда, A – коэффициент, который в общем случае зависит от ряда (дискретный или непрерывный).
Находим значение статистического теста: $$ X_e^2=\sum_{j=1}^k\frac{(f_i-m_i)^2}{m_i} $$ Если эмпирическое значение \(X_e^2\) окажется в критической области, гипотеза \(H_0\) отвергается.
\(X_e^2\geq X_{кр}^2\) - закон распределения не подходит (гипотеза \(H_0\) не принимается)
\(X_e^2\lt X_{кр}^2\) - закон распределения подходит (гипотеза \(H_0\) принимается)
Например:
В эксперименте 60 раз подбрасывают игральный кубик и получают следующие результаты:
| Очки, \(x_i\) | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота, \(f_i\) | 8 | 12 | 13 | 7 | 12 | 8 |
Не является ли кубик фальшивым?
Если кубик не фальшивый, то справедлива гипотеза \(H_0\) - частота выпадений очков подчиняется равномерному распределению: $$ p_i=\frac16,\ \ i=\overline{1,6} $$ При N=60 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_i\cdot N=\frac16\cdot 60=10 $$ по 10 раз.
Строим расчетную таблицу:
| \(x_i\) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| \(f_i\) | 8 | 12 | 13 | 7 | 12 | 8 | 60 |
| \(m_i\) | 10 | 10 | 10 | 10 | 10 | 10 | 60 |
| \(f_i-m_i\) | -2 | 2 | 3 | -3 | 2 | -2 | - |
| \(\frac{(f_i-m_i)^2}{m_i}\) | 0,4 | 0,4 | 0,9 | 0,9 | 0,4 | 0,4 | 3,4 |
Значение теста: $$ X_e^2=3,4 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение:
$$ X_{кр}^2\approx 11,1 $$ Получается, что: $$ X_e^2\lt X_{кр}^2 $$ На уровне значимости α=0,05 принимается гипотеза \(H_0\) про равномерное распределение.
Значит, с вероятностью 95% кубик не фальшивый.
п.6. Примеры
Пример 1. В эксперименте 72 раза подбрасывают игральный кубик и получают следующие результаты:
| Очки, \(x_i\) | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота, \(f_i\) | 8 | 12 | 13 | 7 | 10 | 22 |
Не является ли кубик фальшивым?
Если кубик не фальшивый, то справедлива гипотеза \(H_0\) - частота выпадений очков подчиняется равномерному распределению: $$ p_i=\frac16,\ \ i=\overline{1,6} $$ При N=72 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_i\cdot N=\frac16\cdot 72=12 $$ по 12 раз.
Строим расчетную таблицу:
| \(x_i\) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| \(f_i\) | 8 | 12 | 13 | 7 | 10 | 22 | 72 |
| \(m_i\) | 12 | 12 | 12 | 12 | 12 | 12 | 72 |
| \(f_i-m_i\) | -4 | 0 | 1 | -5 | -2 | 10 | - |
| \(\frac{(f_i-m_i)^2}{m_i}\) | 1,333 | 0,000 | 0,083 | 2,083 | 0,333 | 8,333 | 12,167 |
Значение теста: $$ X_e^2=12,167 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение:
$$ X_{кр}^2\approx 11,1 $$ Получается, что: $$ X_e^2\gt X_{кр}^2 $$ На уровне значимости α=0,05 гипотеза \(H_0\) про равномерное распределение не принимается.
Значит, с вероятностью 95% кубик фальшивый.
Пример 2. Во время Второй мировой войны Лондон подвергался частым бомбардировкам. Чтобы улучшить организацию обороны, город разделили на 576 прямоугольных участков, 24 ряда по 24 прямоугольника.
В течение некоторого времени были получены следующие данные по количеству попаданий на участки:
| Число попаданий, \(x_i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Количество участков, \(f_i\) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 |
Проверялась гипотеза \(H_0\) - стрельба случайна.
Если стрельба случайна, то попадание на участок должно иметь распределение, подчиняющееся «закону редких событий» - закону Пуассона с плотностью вероятности: $$ p(k)=\frac{\lambda^k}{k!}e^{-\lambda} $$ где \(k\) - число попаданий. Чтобы получить значение \(\lambda\), нужно посчитать математическое ожидание данного распределения.
Составим расчетную таблицу:
| \(x_i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| \(x_if_i\) | 0 | 211 | 186 | 105 | 28 | 0 | 0 | 7 | 537 |
$$ \lambda\approx M(x)=\frac{\sum x_if_i}{N}=\frac{537}{576}\approx 0,932 $$ Тогда теоретические частоты будут равны: $$ m_i=N\cdot p(k) $$ Получаем:
| \(x_i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| \(p_i\) | 0,39365 | 0,36700 | 0,17107 | 0,05316 | 0,01239 | 0,00231 | 0,00036 | 0,00005 | 0,99999 |
| \(m_i\) | 226,7 | 211,4 | 98,5 | 30,6 | 7,1 | 1,3 | 0,2 | 0,0 | 576,0 |
| \(f_i-m_i\) | 2,3 | -0,4 | -5,5 | 4,4 | -0,1 | -1,3 | -0,2 | 1,0 | - |
| \(\frac{(f_i-m_i)^2}{m_i}\) (результат) | 0,02 | 0,00 | 0,31 | 0,63 | 0,00 | 1,33 | 0,21 | 34,34 | 36,84 |
Значение теста: \(X_e^2=36,84\)
Поскольку в ходе исследования мы нашли оценку для λ через подсчет выборочной средней, нужно уменьшить число степеней свободы на r=1, и критическое значение статистики искать для \(X_{кр}^2=X^2(\alpha,k-2)\).
Для уровня значимости α=0,05 и k=8, r=1 находим:
\(X_{кр}^2\approx 12,59\)
Получается, что: \(X_e^2\gt X_{кр}^2\)
Гипотеза \(H_0\) не принимается.
Стрельба не случайна.
Пример 3. В предыдущем примере объединили события x={4;5;6;7} с редким числом попаданий:
| Число попаданий, \(x_i\) | 0 | 1 | 2 | 3 | 4-7 |
| Количество участков, \(f_i\) | 229 | 211 | 93 | 35 | 8 |
Проверялась гипотеза \(H_0\) - стрельба случайна.
Для последней объединенной варианты находим среднюю взвешенную: $$ x_5=\frac{4\cdot 7+5\cdot 0+6\cdot 0+7\cdot 1}{7+1}=4,375 $$ Найдем оценку λ.
| \(x_i\) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 8 | 576 |
| \(x_if_i\) | 0 | 211 | 186 | 105 | 35 | 537 |
$$ \lambda\approx M(x)=\frac{\sum x_if_i}{N}=\frac{537}{576}\approx 0,932 $$ Оценка не изменилась, что указывает на правильное определение средней для \(x_5\).
Строим расчетную таблицу для подсчета статистики:
| \(x_i\) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 8 | 576 |
| \(p_i\) | 0,3937 | 0,3670 | 0,1711 | 0,0532 | 0,0121 | 0,9970 |
| \(m_i\) | 226,7 | 211,4 | 98,5 | 30,6 | 7,0 | 574,2 |
| \(f_i-m_i\) | 2,3 | -0,4 | -5,5 | 4,4 | 1,0 | - |
| \(\frac{(f_i-m_i)^2}{m_i}\) | 0,02 | 0,00 | 0,31 | 0,63 | 0,16 | 1,12 |
Значение теста: \(X_e^2=1,12\)
Критическое значение статистики ищем в виде \(X_{кр}^2=X^2(\alpha,k-2)\), где α=0,05 и k=5, r=1
\(X_{кр}^2\approx 7,81\)
Получается, что: \(X_e^2\lt X_{кр}^2\)
Гипотеза \(H_0\) принимается.
Стрельба случайна.
И какой же ответ верный? Полученный в Примере 2 или в Примере 3?
Если посмотреть в расчетную таблицу для статистики \(X_e^2\) в Примере 2, основной вклад внесло слагаемое для \(x_i=7\). Оно равно 34,34 и поэтому сумма \(X_e^2=36,84\) в итоге велика. А в расчетной таблице Примера 3 такого выброса нет. Для объединенной варианты \(x_i=4,375\) слагаемое статистики равно 0,16 и сумма \(X_e^2=1,12\) в итоге мала.
Правильный ответ – в Примере 3.
Стрельба случайна.
