Применение интеграла в стереометрии: объемы тел и площади поверхностей вращения

п.1. Объем тела вращения

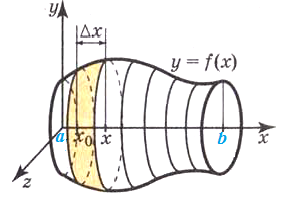Рассмотрим кривую \(y=f(x)\), определенную на отрезке \(a\leq x\leq b\), которая вращается вокруг оси OX. Объем цилиндра высотой \(dx\) и радиусом \(f(x)\), который описывает кривая, равен: $$ dV=\pi f^2(x)\cdot dx $$ Тогда объем всего тела вращения на отрезке [a;b]: $$ V=\int_{a}^{b}=dV=\pi\int_{a}^{b}f^2(x)dx $$

п.2. Длина дуги кривой \(y=f(x)\)

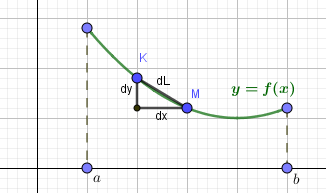Рассмотрим плоскую кривую \(y=f(x)\). Найдем длину дуги этой кривой на отрезке \(a\leq x\leq b\). Выберем на кривой точку \(K, a\leq x_K\leq b\) и рядом с ней точку \(M:\ x_M=x_K+dx\), где \(dx\) – бесконечно малое приращение. Найдем бесконечно малую длину дуги \(KM=dL\)

По теореме Пифагора: $$ dL=\sqrt{(dx)^2+(dy)^2}=dx\sqrt{1+\left(\frac{dy}{dx}\right)^2}=dx\sqrt{1+(y')^2}=dx\sqrt{1+(f'(x))^2} $$ Длина дуги на отрезке [a;b]: $$ L=\int_{a}^{b}dL=\int_{a}^{b}\sqrt{1+(f'(x))^2}dx $$

п.3. Площадь поверхности вращения

Рассмотрим кривую \(y=f(x)\), определенную на отрезке \(a\leq x\leq b\), которая вращается вокруг оси OX.

Площадь боковой поверхности бесконечно малого цилиндра c боковой поверхностью, описываемой дугой длиной \(dL=\sqrt{1+(f'x))^2}dx\), и радиусом \(f(x)\), равна: $$ dS=2\pi f(x)\cdot \sqrt{1+(f'(x))^2}dx $$ Тогда вся площадь поверхности на отрезке [a;b]: $$ S=\int_{a}^{b}dS=2\pi\int_{a}^{b}f(x)\sqrt{1+(f'(x))^2}dx $$

п.4. Примеры

Пример 1. Найдите объем тела, образованного вращением вокруг оси OX фигуры, ограниченной заданными линиями:
a) \(y=-x+2x,\ y=0\)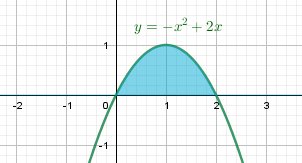

Объем тела вращения: \begin{gather*} V=\pi\int_{0}^{2}(-x^2+2x)^2dx=\pi\int_{0}^{2}\left(x(2-x)\right)^2dx=\pi\int_{0}^{2}\left(x^2(4-4x+x^2)\right)dx=\\ =\pi\int_{0}^{2}(4x^2-4x^3+x^4)dx=\pi\left(\frac{4x^3}{3}-x^4+\frac{x^5}{5}\right)|_{0}^{2}=\pi\left(\frac{32}{3}-16+\frac{32}{5}-0\right)=\frac{16}{15}\pi \end{gather*}
б) \(y=2x+1,\ x=1,\ x=4,\ y=0\)

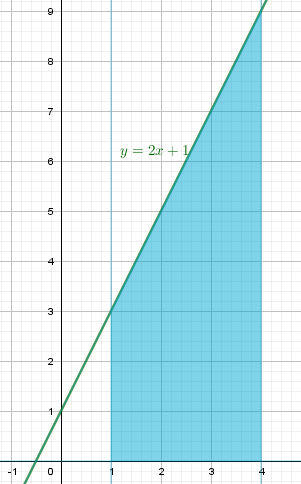Объем тела вращения: \begin{gather*} V=\pi\int_{1}^{4}(2x+1)^2dx=\\ =\pi\int_{1}^{4}(4x^2+4x+1)dx=\\ =\pi\left(\frac{4x^3}{3}+2x^2+x\right)|_{1}^{4}=\\ =\pi\left(\frac{256}{3}+32+4-\frac43-2-1\right)117\pi \end{gather*}

Ответ: a) \(\frac{16}{15}\pi\) б) \(117\pi\)

Пример 2*. Равносторонний треугольник со стороной 10 см вращается около внешней оси, параллельной стороне треугольника и отстоящей от нее на расстоянии, равной половине высоты треугольника. Найдите объем тела вращения.

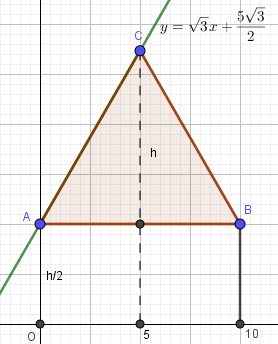Высота правильного треугольника: \(h=a sin⁡60^\circ=\frac{\sqrt{3}}{2}a\) При \(a=10\) высота \(h=5\sqrt{3}\). Координаты точки \(A(0;2,5\sqrt{3})\). Для точки \(C:\ x=5,\ y=\frac32 h=7,5\sqrt{3}\) Уравнение прямой AC: \begin{gather*} \frac{x-x_A}{x_C-x_A}=\frac{y-y_A}{y_C-y_A}\\ \frac{x-0}{5-0}=\frac{y-2,5\sqrt{3}}{y,5\sqrt{3}-2,5\sqrt{3}}\\ \frac{5\sqrt{3}x}{5}=y-2,5\sqrt{3}\\ y=\sqrt{3}x+\frac{5\sqrt{3}}{2} \end{gather*}

Объем всего внешнего тела вращения равен удвоенному объему тела, образованного при вращении прямой AC на интервале \(0\leq x\leq 5\): \begin{gather*} V_1=2\cdot \pi\int_{0}^{5}\left(\sqrt{3}x+\frac{5\sqrt{3}}{2}\right)^2dx=2\pi\int_{0}^{5}\left(\sqrt{3}\left(x+\frac52\right)\right)^2=6\pi\int_{0}^{5}\left(x^2+5x+\frac{25}{4}\right)dx=\\ =6\pi\left(\frac{x^3}{3}+\frac{5x^2}{2}+\frac{25}{4}x\right)|_{0}^{5}=6\pi\left(\frac{125}{3}+\frac{125}{2}+\frac{125}{4}-0\right)=\frac{1625}{2}\pi \end{gather*} Внутри образуется полый цилиндр объемом: \begin{gather*} V_2=\pi\cdot\left(\frac h2\right)^2\cdot 10=\pi\cdot\left(\frac{5\sqrt{3}}{2}\right)^2\cdot 10=\frac{375}{2}\pi \end{gather*} Итоговый объем: \begin{gather*} V=V_1-V_2=\frac{1625}{2}\pi-\frac{375}{2}\pi=625\pi \end{gather*} Ответ: \(625\pi\)

Пример 3. Найдите площадь поверхности вращения, образованной вращением вокруг оси OX фигуры, ограниченной заданными линиями:
a) \(y=\sqrt{9-x^2},\ y=0\)

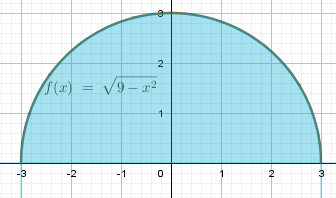Поверхностью вращения будет сфера. Найдем множитель длины дуги: $$ L=\sqrt{1+\left(f'(x)\right)^2} $$

\begin{gather*} f'(x)=\frac{1}{2\sqrt{9-x^2}}\cdot (9-x^2)'=\frac{x}{\sqrt{9-x^2}}\\ 1+\left(f'(x)\right)^2=1+\left(\frac{x}{\sqrt{9-x^2}}\right)^2=1+\frac{x^2}{9-x^2}=\frac{9-x^2+x^2}{9-x^2}=\frac{9}{9-x^2} \end{gather*} Площадь поверхности: \begin{gather*} S=2\pi\int_{-3}^{3}\sqrt{9-x^2}\cdot\sqrt{\frac{9}{9-x^2}}dx=2\pi\int_{-3}^{3}3dx=6\pi\cdot x|_{-3}^{3}=6\pi(3+3)=36\pi \end{gather*}

б) \(y=x+1,\ y=0,\ x=0,\ x=2\)

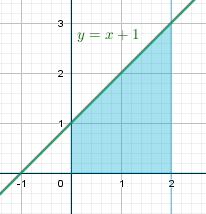Поверхностью вращения будет боковая поверхность усеченного конуса. Найдем множитель длины дуги: \( L=\sqrt{1+\left(f'(x)\right)^2}\) $$ f'(x)=1,\ 1+\left(f'(x)\right)^2=1+1=2,\ L=\sqrt{2} $$

Площадь поверхности: \begin{gather*} S=2\pi\int_{0}^{2}(x+1)\cdot\sqrt{2}dx=2\sqrt{2}\pi\int_{0}^{2}(x+1)dx=2\sqrt{2}\pi\left(\frac{x^2}{2}+x\right)|_{0}^{2}=\\ =2\sqrt{2}\pi(2+2-0)=8\sqrt{2}\pi \end{gather*}
Ответ: a) \(36\pi\) б) \(8\sqrt{2}\pi\)

Пример 4. Найдите путь, который пройдет тело от \(x_0=0\) до возвращения в исходную точку, если его траектория описывается уравнением \(x(t)=\sqrt{16-t^2}\).

Тело совершило разворот и вернулось в исходную точку. Найдем отрезок времени, на котором совершалось это движение. Решим уравнение: $$ \sqrt{16-t^2}=0\Rightarrow t^2=16\Rightarrow t=\pm 4 $$ Отрезок времени: \(t\in\left[-4;4\right]\). Находим путь – длину дуги траектории: \begin{gather*} s=\int_{-4}^{4}\sqrt{1+(x'(t))^2}dt\\ x'(t)=\frac{1}{2\sqrt{16-t^2}}\cdot (16-t^2)'=\frac{-2t}{2\sqrt{16-t^2}}=-\frac{t}{\sqrt{16-t^2}}\\ 1+(x'(t))^2=1+\left(-\frac{t}{\sqrt{16-t^2}}\right)^2=1+\frac{t^2}{16-t^2}=\frac{16-t^2+t^2}{16-t^2}=\frac{16}{16-t^2}\\ \sqrt{1+(x'(t))^2}=\frac{4}{\sqrt{16-t^2}}=\frac{4}{\sqrt{16\left(1-\left(\frac t4\right)^2\right)}}=\frac{4}{4\sqrt{1-\left(\frac t4\right)^2}}=\frac{1}{\sqrt{1-\left(\frac t4\right)^2}} \end{gather*} Используем табличный интеграл: \(\int\frac{1}{\sqrt{1-x^2}}=arcsinx+C\)
Множитель \(\frac14\) перед аргументом \(t\) даст 4 перед интегралом.
Получаем: \begin{gather*} s=\int_{-4}^{4}\frac{1}{\sqrt{1-\left(\frac t4\right)^2}}dt=4\cdot arcsin\left(\frac t4\right)|_{-4}^{4}=4(arcsin1-arcsin(-1))=\\ =4(arcsin1+arcsin1)=8arcsin1=8\cdot\frac\pi 2=4\pi \end{gather*} Ответ: \(4\pi\)

Примечание:

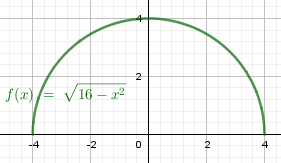Разумеется, все будет гораздо проще, если заметить, что тело движется по полуокружности радиусом 4. Длина полуокружности \(\frac L2=\pi R=4\pi\). Но на практике траектории гораздо сложней, и тогда уже без общей формулы не обойдёшься. И решение часто находится не аналитически, а с помощью численных методов.