Главная Справочник Алгебра 10-11 класс Предел функции

Предел функции

Предел функции в точке и на бесконечности
Свойства предела функции
Раскрытие неопределенностей $\left[\frac{\infty}{\infty}\right]$ и $\left[\infty-\infty\right]$
Раскрытие неопределенности $\left[\frac{0}{0}\right]$
Примеры

п.1. Предел функции в точке и на бесконечности

Понятие предела функции является обобщением понятия предела последовательности (см. §36 данного справочника). Определения предела функции в точке и на бесконечности даны в этом параграфе на « языке ε-δ» , в традиции, заложенной великим французским математиком Коши.

Число $a$ называют пределом функции $f(x)$ в точке $x_0$, если для любого $\varepsilon\gt 0$ найдется соответственное ему $\delta=\delta(\varepsilon)\gt 0$, такое, что для всех аргументов $x,\ 0\lt |x-x_0|\lt \delta$ выполняется неравенство $|f(x)-a|\lt\varepsilon$. \begin{gather*} \lim_{x\rightarrow x_0}f(x)=a\Leftrightarrow \forall \varepsilon \gt 0\ \exists\delta=\delta(\varepsilon)\gt 0: \forall x,\ 0\lt|x-x_0|\lt \delta\Rightarrow |f(x)-a|\lt \varepsilon \end{gather*}

Пусть функция $f(x)$ задана на множестве $\chi$, в котором для любого числа $\delta$ найдётся элемент, лежащий правее его. В этом случае число $a$ называют пределом функции $f(x)$ на плюс бесконечности, если для любого $\varepsilon\gt 0$ найдется соответственное ему $\delta=\delta(\varepsilon)\gt 0$, такое, что для всех аргументов, лежащих правее $\delta$, справедливо неравенство $|f(x)-a|\lt \varepsilon$. \begin{gather*} \lim_{x\rightarrow +\infty}f(x)=a\Leftrightarrow \forall \varepsilon \gt 0\ \exists\delta=\delta(\varepsilon)\gt 0:\ \forall x\in \chi, x\gt \delta\Rightarrow |f(x)-a|\lt \varepsilon \end{gather*}

Пусть функция $f(x)$ задана на множестве $\chi$, в котором для любого числа $\delta$ найдётся элемент, лежащий левее его. В этом случае число $a$ называют пределом функции $f(x)$ на минус бесконечности, если для любого $\varepsilon\gt 0$ найдется соответственное ему $\delta=\delta(\varepsilon)\gt 0$, такое, что для всех аргументов, лежащих левее $(-\delta)$, справедливо неравенство $|f(x)-a|\lt \varepsilon$. \begin{gather*} \lim_{x\rightarrow -\infty}f(x)=a\Leftrightarrow \forall \varepsilon \gt 0\ \exists\delta=\delta(\varepsilon)\gt 0:\ \forall x\in \chi, x\gt -\delta\Rightarrow |f(x)-a|\lt \varepsilon \end{gather*}

п.2. Свойства предела функции

1. Одна и та же функция в одной и той же точке может иметь только один предел: \begin{gather*} \left. \begin{array}{r} \lim_{x\rightarrow x_0}f(x)=a\\ \lim_{x\rightarrow x_0}f(x)=b \end{array} \right\} \Rightarrow a=b \end{gather*} 2. Если функция непрерывна, то её предел в точке $x_0$ совпадает со значением функции в этой точке: \begin{gather*} \lim_{x\rightarrow x_0}f(x)=f(x_0) \end{gather*} 3. Если функция «зажата» между двумя другими функциями, имеющими одинаковый предел $a$, то предел этой функции также равен $a$: \begin{gather*} \left. \begin{array}{r} g(x)\leq f(x)\leq h(x)\\ \lim_{x\rightarrow x_0}g(x)=a\\ \lim_{x\rightarrow x_0}h(x)=b \end{array} \right\} \Rightarrow \lim_{x\rightarrow x_0}f(x)=a \end{gather*} 4. Операция перехода к пределу сохраняет нестрогие неравенства: \begin{gather*} \left. \begin{array}{r} f(x)\leq g(x)\\ \lim_{x\rightarrow x_0}f(x)=a\\ \lim_{x\rightarrow x_0}g(x)=b \end{array} \right\} \Rightarrow a\leq b \end{gather*} 5. Переход к пределу для строгих неравенств в общем случае приводит к нестрогому неравенству: \begin{gather*} \left. \begin{array}{r} f(x)\lt g(x)\\ \lim_{x\rightarrow x_0}f(x)=a\\ \lim_{x\rightarrow x_0}g(x)=b \end{array} \right\} \Rightarrow a\leq b \end{gather*} 6. Предел суммы (разности, произведения, частного) равен сумме (разности, произведению, частному) пределов: \begin{gather*} \left. \begin{array}{r} \lim_{x\rightarrow x_0}f(x)=a\\ \lim_{x\rightarrow x_0}g(x)=b \end{array} \right\} \Rightarrow \lim_{x\rightarrow x_0}(f(x)\pm g(x))=a\pm b \\ \left. \begin{array}{r} \lim_{x\rightarrow x_0}f(x)=a\\ \lim_{x\rightarrow x_0}g(x)=b \end{array} \right\} \Rightarrow \lim_{x\rightarrow x_0}(f(x)\cdot g(x))=a\cdot b \\ \left. \begin{array}{r} \lim_{x\rightarrow x_0}f(x)=a\\ \lim_{x\rightarrow x_0}g(x)=b\ne 0 \end{array} \right\} \Rightarrow \lim_{x\rightarrow x_0}\left(\frac{f(x)}{g(x)}\right)=\frac ab \end{gather*}

п.3. Раскрытие неопределенностей $\left[\frac{\infty}{\infty}\right]$ и $\left[\infty-\infty\right]$

Для пределов функций правила раскрытия неопределенностей $\left[\frac{\infty}{\infty}\right]$ и $\left[\infty-\infty\right]$ аналогичны правилам для пределов последовательностей (см. §37 данного справочника).

Чтобы раскрыть неопределенность $\left[\frac{\infty}{\infty}\right]$ от частного двух многочленов $P_k(x)$ и $Q_p(x)$, нужно вынести за скобки x в максимальной степени $m=max(k,p)$.
В общем случае, это правило справедливо не только для целых, но и для рациональных, а также действительных степеней k и p.

Например:
Найдем предел $\lim_{x\rightarrow\infty}\frac{x^3+x^2-8}{1+3x^3}$ $$ \lim_{x\rightarrow\infty}\frac{x^3+x^2-8}{1+3x^3} =\left[\frac{\infty}{\infty}\right]= \lim_{x\rightarrow\infty}\frac{x^3\left(1+\frac 1x-\frac{8}{x^3}\right)}{x^3\left(\frac{1}{x^3}+3\right)} = \lim_{x\rightarrow\infty}\frac{1+\frac 1x-\frac{8}{x^3}}{\frac{1}{x^3}+3}= \frac{1+0-0}{0+3}=\frac13 $$ Ответ: $\frac13$

Чтобы раскрыть неопределенность вида $\left[\infty-\infty\right]$, рекомендуется умножить и разделить функцию от x под знаком предела на сопряженное выражение.

Например:
Найдем предел $\lim_{x\rightarrow\infty}(\sqrt{x-4}-\sqrt{x})$ \begin{gather*} \lim_{x\rightarrow\infty}(\sqrt{x-4}-\sqrt{x})= \left[\infty-\infty\right] =\lim_{x\rightarrow\infty}\frac{(\sqrt{x-4}-\sqrt{x})(\sqrt{x-4}+\sqrt{x})}{(\sqrt{x-4}+\sqrt{x})}=\\ =\lim_{x\rightarrow\infty}\frac{x-4-x}{\sqrt{x-4}+\sqrt{x}}=-4\cdot \lim_{x\rightarrow\infty}\frac{1}{\sqrt{x-4}+\sqrt{x}}= -4\cdot\frac{1}{\infty+\infty}=-4\cdot 0=0 \end{gather*} Ответ: 0

п.4. Раскрытие неопределенности $\left[\frac00\right]$

Чтобы раскрыть неопределенность $\left[\frac00\right]$ возникшую при $x\rightarrow x_0$ в рациональном дробном выражении, рекомендуется вынести в числителе и знаменателе множители $(x-x_0)$ и сократить их.

Например:
Найдем предел $\lim_{x\rightarrow 4}\frac{x^2-16}{x-6x+8}$ $$ \lim_{x\rightarrow 4}\frac{x^2-16}{x-6x+8}=\left[\frac00\right] =\lim_{x\rightarrow 4}\frac{(x-4)(x+4)}{(x-4)(x-2)}=\lim_{x\rightarrow 4}\frac{x+4}{x-2}=\frac{4+4}{4-2}=4 $$ Ответ: 4

Чтобы раскрыть неопределенность $\left[\frac00\right]$ возникшую при $x\rightarrow x_0$ в иррациональном дробном выражении, рекомендуется умножить числитель и знаменатель на сопряженное выражение, а затем вынести в числителе и знаменателе множители $(x-x_0)$ и сократить их.

Например:
Найдем предел $\lim_{x\rightarrow 1}\frac{\sqrt{1+5x}-3}{\sqrt{x}-1}$
\begin{gather*} \lim_{x\rightarrow 1}\frac{\sqrt{1+5x}-3}{\sqrt{x}-1} = \left[\frac00\right] =\lim_{x\rightarrow 1}\frac{(\sqrt{1+8x}-3)(\sqrt{1+8x}+3)(\sqrt{x}+1)}{(\sqrt{x}-1)(\sqrt{1+8x}+3)(\sqrt{x}+1)} =\\ =\lim_{x\rightarrow 1}\frac{(1+8x-3^2)(\sqrt{x}+1)}{(x-1)(\sqrt{1+8x}+3)} =\lim_{x\rightarrow 1}\frac{8(x-1)(\sqrt{x}+1)}{(x-1)(\sqrt{1+8x}+3)}=\\ =8\lim_{x\rightarrow 1}\frac{\sqrt{x}+1}{\sqrt{1+8x}+3}=8\cdot\frac{1+1}{3+3}=\frac83=2\frac23 \end{gather*} Ответ: $2\frac23$

п.5. Примеры

Пример 1. Докажите, используя определение предела функции в точке:
a) $ \lim_{x\rightarrow 1}(3x+1)=4 $

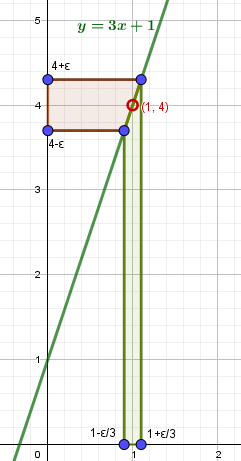Пусть $\varepsilon\gt 0$ – сколь угодно малое число.
Найдем множество значений x, для которых $|f(x)-a|\lt \varepsilon$.
Подставляем $f(x)=3x+1,\ a=4$: \begin{gather*} |(3x+1)-4|\lt\varepsilon\Rightarrow |3x-3|\lt\varepsilon\Rightarrow 3|x-1|\lt\varepsilon\\ |x-1|\lt\frac{\varepsilon}{3}\Rightarrow -\frac{\varepsilon}{3}\lt x-1\lt\frac{\varepsilon}{3}\\ 1-\frac{\varepsilon}{3}\lt x\lt 1+\frac{\varepsilon}{3} \end{gather*} Найдем $\delta$-окрестность для x: \begin{gather*} |x-x_0|\lt\delta\Rightarrow -\delta\lt x-x_0\lt\delta\\ -\frac{\varepsilon}{3}\lt x-1\lt\frac{\varepsilon}{3}\Rightarrow 0\lt |x-1|\lt\frac{\varepsilon}{3}\\ \delta(\varepsilon)=\frac{\varepsilon}{3} \end{gather*}

Например:

ε	0,1	0,01	0,001	0,0001	0,00001	0,000001
$\delta(\varepsilon)$	0,033	0,0033	0,00033	0,000033	3,3·10^-6	3,3·10^-7

Таким образом, для любого сколь угодно малого ε>0 мы находим $\delta(\varepsilon)=\frac{\varepsilon}{3}$, при этом из $0\lt|x-1|\lt\delta(\varepsilon)\Rightarrow |(3x+1)-4|\lt\varepsilon$.
Что и требовалось доказать.

б) $ \lim_{x\rightarrow 5}(x^2-1)=24 $

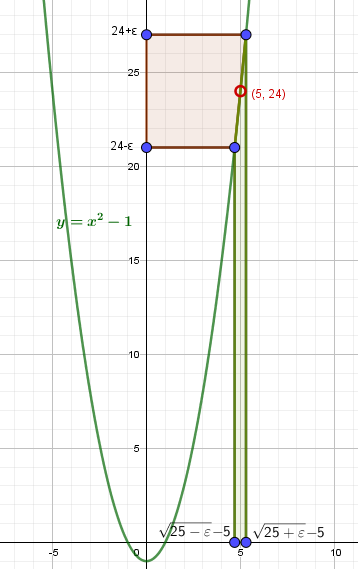Пусть $\varepsilon\gt 0$ – сколь угодно малое число.
Найдем множество значений x, для которых $|f(x)-a|\lt \varepsilon$.

Подставляем $f(x)=x^2-1,\ a=24$: \begin{gather*} |(x^2-1)-24|\lt\varepsilon\\ |x^2-25|\lt\varepsilon\\ -\varepsilon\lt x^2-25\lt\varepsilon\\ 25-\varepsilon\lt x^2\lt 25+\varepsilon\\ \sqrt{25-\varepsilon}\lt x\lt\sqrt{25+\varepsilon} \end{gather*} Найдем $\delta$-окрестность для x: \begin{gather*} |x-x_0|\lt\delta\Rightarrow -\delta\lt x-x_0\lt\delta\\ \sqrt{25-\varepsilon}-5\lt x-5\lt\sqrt{25+x}-5\\ -\delta_1\lt x-5\lt\delta_2\\ \delta_1=5-\sqrt{25-\varepsilon}\\ \delta_2=\sqrt{25+\varepsilon}-5 \end{gather*}

Выбираем в качестве $\delta(\varepsilon)$ меньшую оценку $\delta_2$: \begin{gather*} \delta(\varepsilon)=min(5-\sqrt{25-\varepsilon};\sqrt{25+\varepsilon}-5)=\delta_2=\sqrt{25+\varepsilon}-5\\ 0\lt|x-5|\lt\sqrt{25+\varepsilon}-5\\ \delta(\varepsilon)=\sqrt{25+\varepsilon}-5 \end{gather*} Например:

ε	0,1	0,01	0,001	0,0001	0,00001	0,000001
$\delta(\varepsilon)$	0,01	0,001	0,0001	0,00001	10^-6	10^-7

Таким образом, для любого сколь угодно малого ε>0 мы находим $\delta(\varepsilon)=\sqrt{25+\varepsilon}-5$, при этом из $0\lt|x-1|\lt\delta(\varepsilon)\Rightarrow |(x^2-1)-24|\lt\varepsilon$.
Что и требовалось доказать.

Пример 2. Найдите пределы функций, используя свойства пределов и правила раскрытия неопределенностей вида $\left[\frac{\infty}{\infty}\right],\ \left[\infty-\infty\right]$ и $\left[\frac00\right]$:
a) $ \lim_{x\rightarrow\infty}\frac{x^2-3x+2}{3x^2-5x-2} $ \begin{gather*} \lim_{x\rightarrow\infty}\frac{x^2-3x+2}{3x^2-5x-2}= \left[\frac{\infty}{\infty}\right] = \lim_{x\rightarrow\infty}\frac{x^2\left(1-\frac3x+\frac{2}{x^2}\right)}{x^2\left(3-\frac5x-\frac{2}{x^2}\right)} = \lim_{x\rightarrow\infty}\frac{1-\frac3x+\frac{2}{x^2}}{3-\frac5x-\frac{2}{2x}}=\frac{1-0+0}{3-0-0}=\frac13 \end{gather*} б) $ \lim_{x\rightarrow\infty}\frac{\sqrt[3]{x^3+1}+\sqrt{x^2-1}}{2x-7} $ \begin{gather*} \lim_{x\rightarrow\infty}\frac{\sqrt[3]{x^3+1}+\sqrt{x^2-1}}{2x-7}= \left[\frac{\infty}{\infty}\right] = \lim_{x\rightarrow\infty}\frac{x\left(\sqrt[3]{\frac{x^3}+1}{x^3}+\sqrt{\frac{x^2-1}{x^2}}\right)}{x\left(2-\frac7x\right)}= \\ =\lim_{x\rightarrow\infty}\frac{\sqrt[3]{1+\frac{1}{x^3}}+\sqrt{1-\frac{1}{x^2}}}{2-\frac7x}= \frac{\sqrt[3]{1+0}+\sqrt{1-0}}{2-0}=1 \end{gather*} в) $ \lim_{x\rightarrow\infty}(x\sqrt{x^2+2}-x^2) $ \begin{gather*} \lim_{x\rightarrow\infty}(x\sqrt{x^2+2}-x^2)=\left[\infty-\infty\right] = \lim_{x\rightarrow\infty}\frac{x(\sqrt{x^2+2}-x)(\sqrt{x^2+2}+x)}{(\sqrt{x^2+2}+x)}=\\ =\lim_{x\rightarrow\infty}\frac{\left((x^2+2)-x^2\right)}{\sqrt{x^2+2}+x}= \lim_{x\rightarrow\infty}\frac{2x}{x\left(\sqrt{\frac{x^2+2}{x^2}}+1\right)}= 2\lim_{x\rightarrow\infty}\frac{1}{\sqrt{1+\frac{2}{x^2}}+1}=\\ =2\cdot\frac{1}{\sqrt{1+0}+1}=1 \end{gather*} г) $ \lim_{x\rightarrow 2}\frac{x^2-3x+2}{3x^2-5x-2} $ \begin{gather*} \lim_{x\rightarrow 2}\frac{x^2-3x+2}{3x^2-5x-2}=\left[\frac00\right] = \lim_{x\rightarrow 2}\frac{(x-1)(x-2)}{(3x+1)(x-2)} =\lim_{x\rightarrow 2}\frac{(x-1)}{(3x+1)} = \frac{2-1}{6+1}=\frac17 \end{gather*} д) $ \lim_{x\rightarrow 6}\frac{2-\sqrt{x-2}}{x^2-36} $ \begin{gather*} \lim_{x\rightarrow 6}\frac{2-\sqrt{x-2}}{x^2-36}=\left[\frac00\right] = \lim_{x\rightarrow 6}\frac{(2-\sqrt{x-2})(2+\sqrt{x-2})}{(x^2-36)(2+\sqrt{x-2})}=\\ \lim_{x\rightarrow 6}\frac{2^2-(x-2)}{(x^2-36)(2+\sqrt{x-2})} = \lim_{x\rightarrow 6}\frac{6-x}{(x-6)(x+6)(2+\sqrt{x-2})} =\\ \lim_{x\rightarrow 6}\frac{1}{(x+6)(2+\sqrt{x-2})}= \frac{1}{(6+6)(2+2)} = \frac{1}{48} \end{gather*} Ответ: a) $\frac13$; б) 1; в) 1; г) $\frac17$; д) $\frac{1}{48}$

Рейтинг пользователей

за неделю

за неделю
один месяц
три месяца

Помогай другим

Отвечай на вопросы и получай ценные призы каждую неделю

См. подробности

Предел функции

п.1. Предел функции в точке и на бесконечности

п.2. Свойства предела функции

п.3. Раскрытие неопределенностей \(\left[\frac{\infty}{\infty}\right]\) и \(\left[\infty-\infty\right]\)

п.4. Раскрытие неопределенности \(\left[\frac00\right]\)

п.5. Примеры

Рейтинг пользователей