Показательные неравенства и системы
п.1. Определение показательного неравенства
Например:
\(5^{x^2+2}\gt 5^3,\ \ \left(\frac13\right)^{\sqrt{x-4}}\leq\frac{1}{\sqrt{3}}\)
Если \(0\lt a\lt 1\), то показательное неравенство \(a^{f(x)}\gt a^{g(x)}\) равносильно неравенству \(f(x)\lt g(x)\) (знак меняется на противоположный).
Например:
1) \(5^{x^2+2}\gt 5^3\Leftrightarrow x^2+2\gt 3\Leftrightarrow x^2\gt 1\Leftrightarrow x\lt -1\cup x\gt 1\)
Мы получили решение: \(x\in(-\infty;-1)\cup(1;+\infty)\)
2) \(\left(\frac13\right)^{\sqrt{x-4}}\leq\frac{1}{\sqrt{3}}\Leftrightarrow \left(\frac13\right)^{\sqrt{x-4}}\leq\left(\frac13\right)^{1/2}\Leftrightarrow \sqrt{x-4}\geq \frac12\Leftrightarrow \begin{cases} x-4\geq\frac14\\ x-4\geq 9 \end{cases} \Leftrightarrow x\geq 4\frac14 \)
Мы получили решение: \(x\in\left.\left[4\frac14; +\infty\right.\right)\)
п.2. Методы решения показательных неравенств
Для решения показательных неравенств применяются следующие методы:
1) переход от неравенства между \(a^{f(x)}\) и \(a^{g(x)}\) к равносильному неравенству между \(f(x)\) и \(g(x)\), где знаки определяются значением a (см. определение выше);
2) графический метод;
3) замена переменной.
п.3. Примеры
Пример 1. Решите неравенство:
a) \(\left(\frac18\right)^{-5x}\lt 32\)
\((2^{-3})^{-5x}\lt 2^5\)
\(2^{15x}\lt 2^5\)
\(15x\lt 5\)
\(x\lt \frac13\)
Ответ: \(x\in\left(-\infty;\frac13\right)\)
б) \(5^{\frac{x+2}{x-3}}\leq 5\)
\(\frac{x+2}{x-3}\leq 1\)
\(\frac{x+2}{x-3}-1\leq 0\)
\(\frac{x+2-(x-3)}{x-3}\leq 0\)
\(\frac{5}{3-x}\leq 0\)
\(x-3\lt 0\) (знаменатель не может быть равен 0)
\(x\lt 3\)
Ответ: \(x\in(-\infty;3)\)
в) \((0,64)^{0,5x^2-3}\geq\left(\frac54\right)^{-3}\)
\((0,8^2)^{0,5x^2-3}\geq \left(\frac45\right)^3\)
\(\left(\frac45\right)^{2(0,5x^2-3)}\geq\left(\frac45\right)^3\)
\(2(0,5x^2-3)\leq 3\)
\((x+3)(x-3)\leq 0\)
Решаем методом интервалов (см. §7 справочника для 9 класса)
\(-3\leq x\leq 3\)
Ответ: \(x\in[-3;3]\)
г) \(\sqrt{64}\cdot 4^{-6x^2}\geq 16^{4x}\)
\(4^{3\cdot\frac12}\cdot 4^{-6x^2}\leq 4^{2\cdot 4x}\)
\(4^{-6x^2+1,5}\leq 4^{8x}\)
\(-6x^2+1,5\leq 8x\)
\(6x^2+8x-1,5\geq 0\)
\(D=8^2-4\cdot 6\cdot (-1,5)=64+36=100\)
\(x=\frac{-8\pm 10}{12}= \left[ \begin{array}{l l} -1,5\\ \frac16 \end{array} \right. \)
\((x+1,5)\left(x-\frac16\right)\geq 0\)
\(x\leq -1,5\cup x\geq\frac16\)
Ответ: \(x\in\left.\left(-\infty;1,5\right.\right]\cup\left.\left[\frac16;+\infty\right.\right)\)
д) \(0,7^{\frac{x+7}{x^2-9}}\gt 1\)
\(0,7^{\frac{x+7}{x^2-9}}\gt 0,7^0\)
\(\frac{x+7}{x^2-9}\lt 0\)
\(\frac{x+7}{(x+3)(x-3)}\lt 0\)
\((x+1,5)\left(x-\frac16\right)\geq 0\)
\(x\lt-7\cup -3\lt x\lt 3\)
Ответ: \(x\in(-\infty;-7)\cup(-3;3)\)
e) \(9^{x+1}-2\cdot 3^x\lt 7\)
\(9\cdot 9^x-2\cdot 3^x\lt 7\)
Замена: \(t=3^x\gt 0\)
\( \begin{cases} 9t^2-2t-7\lt 0\\ t\gt 0 \end{cases} \Rightarrow \begin{cases} (9t+7)(t-1)\lt 0\\ t\gt 0 \end{cases} \Rightarrow \begin{cases} \left(t+\frac79\right)(t-1)\lt 0\\ t\gt 0 \end{cases} \)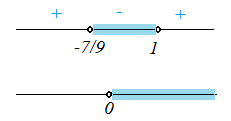
Получаем пересечение отрезка и луча: \(0\lt t\lt 1\)
Возвращаемся к исходной переменной: \(0\lt 3^x\lt 1\Rightarrow 3^x\lt 3^0\Rightarrow x\lt 0\)
Ответ: \(x\in(-\infty;0)\)
Пример 2*. Решите неравенство:
a) \(-3\leq 3^{x^2-8}-6\leq 3\)
\(-3+6\leq 3^{x^2-8}\leq 3+6\)
\(3\leq 3^{x^2-8}\leq 9\)
\(1\leq x^2-8\leq 2\)
\(9\leq x^2\leq 10\)
Берем корень с каждого члена неравенства, при этом \(\sqrt{x^2}=|x|\).
Получаем: \(3\leq |x|\leq\sqrt{10}\)
\(-\sqrt{10}\leq x\leq -3\cup 3\leq x\leq \sqrt{10}\)
Ответ: \(x\in[-\sqrt{10};-3]\cup[3;\sqrt{10}]\)
б) \(4^x-2^{2(x-1)}+8^{\frac23(x-2)}\gt 52\)
\(4^x-4^{x-1}+2^{3\cdot\frac23(x-2)}\gt 52\)
\(4^x-4^{x-1}+4^{x-2}\gt 52\)
\(4^x\left(1-\frac14+\frac{1}{16}\right)\gt 52\)
\(4^x\cdot\frac{13}{16}\gt 52\)
\(4^x\gt 4^x\)
\(x\gt 3\)
Ответ: \(x\in(3;+\infty)\)
в) \(\frac{2^x-8}{x^2-7x+10}\geq 0\)
Получаем совокупность систем: $$ \left[ \begin{array}{l l} \begin{cases} 2^x-8\geq 0\\ x^2-7x+10\lt 0 \end{cases} \\ \begin{cases} 2^x-8\leq 0\\ x^2-7x+10\gt 0 \end{cases} \end{array} \right. \Rightarrow \left[ \begin{array}{l l} \begin{cases} 2^x\geq 8\\ (x-2)(x-5)\lt 0 \end{cases} \\ \begin{cases} 2^x\leq 8\\ (x-2)(x-5)\gt 0 \end{cases} \end{array} \right. \Rightarrow \left[ \begin{array}{l l} \begin{cases} x\geq 3\\ (x-2)(x-5)\lt 0 \end{cases} \\ \begin{cases} x\leq 3\\ (x-2)(x-5)\gt 0 \end{cases} \end{array} \right. $$ 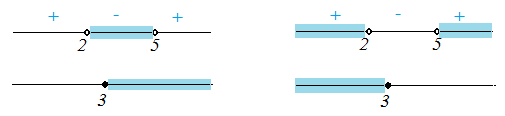
В системах (с фигурными скобками) ищем пересечение, в совокупности (квадратная скобка) ищем объединение. Получаем: \(3\leq x\lt 5\cup x\lt 2\)
По возрастанию: \(x\lt 2\cup 3\leq x\lt 5\)
Ответ: \(x\in(-\infty;2)\cup\left.\left[3;5\right.\right)\)
г) \(1\lt 3^{|x^2-x|}\lt 9\)
\(3^0\lt 3^{|x^2-x|}\lt 3^2\) $$ 0\lt |x^2-x|\lt 2\Rightarrow \begin{cases} |x^2-x|\gt 0\\ |x^2-x|\lt 2 \end{cases} \Rightarrow \begin{cases} x^2-x\ne 0\\ -2\lt x^2-x\lt 2 \end{cases} \Rightarrow \begin{cases} x(x-1)\ne 0\\ x^2-x+2\gt 0\\ x^2-x-2\lt 0 \end{cases} $$ Неравенство \(x^2-x+2\gt 0\) при \(D\lt 0\) выполняется для любого \(x\in\mathbb{R}\). $$ \begin{cases} x\ne {0;1}\\ D=-7\lt 0,\ x\in\mathbb{R}\\ (x-2)(x+1)\lt 0 \end{cases} \Rightarrow \begin{cases} x\ne {0;1}\\ (x-2)(x+1)\lt 0 \end{cases} $$ 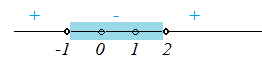
\(-1\lt x\lt 0\cup 0\lt x\lt 1\cup 1\lt x\lt 2\)
Ответ: \(x\in(-1;0)\cup (0;1)\cup (1;2)\)
д) \(2^{\sqrt{x}+1}-3^{\sqrt{x}}\gt 3^{\sqrt{x}-1}-2^{\sqrt{x}}\)
\(2^{\sqrt{x}+1}+2^{\sqrt{x}}\gt 3^{\sqrt{x}-1}+3^{\sqrt{x}}\)
\(2^{\sqrt{x}}(2+1)\gt 3^{\sqrt{x}}\left(\frac13+1\right)\)
\(\frac{2^{\sqrt{x}}}{3^{\sqrt{x}}}\gt \frac43 : 3\)
\(\left(\frac23\right)^{\sqrt{x}}\gt\left(\frac23\right)^2\)
\(\sqrt{x}\lt 2\)
\( \begin{cases} x\lt 4\\ x\geq 0 \end{cases} \Rightarrow 0\leq x\lt 4 \)
Ответ: \(x\in\left.\left[0;4\right.\right)\)
e) \((2x-1)^x\geq (2x-1)^{x^2-2}\)
ОДЗ: \(2x-1\gt 0\Rightarrow x\gt\frac12\)
1) Если \(2x-1=1\), то степень не важна.
Слева и справа будет получаться 1, равенство выполняется
\(2x-1=1\Rightarrow x=1\)
\(2)\ \begin{cases} 0\lt 2x-1\lt 1\\ x\leq x^2-2 \end{cases} \Rightarrow \begin{cases} 1\lt 2x\lt 2\\ x^2-x-2\geq 0 \end{cases} \Rightarrow \begin{cases} \frac12\lt x\lt 1\\ (x-2)(x+1)\geq 0 \end{cases} \)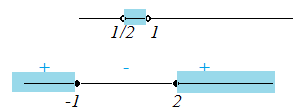
Решений нет, \(x\in\varnothing\)
\(3)\ \begin{cases} 2x-1\gt 1\\ x\geq x^2-2 \end{cases} \Rightarrow \begin{cases} x\gt 1\\ (x-2)(x+1)\leq 0 \end{cases} \)
\(1\lt x\leq 2\)
Получаем: \(x=1\cup 1\lt x\leq 2,\ \text{т.е.}\ 1\leq x\leq 2\)
Ответ: \(x\in[1;2]\)
Пример 3*. Решите систему. Найдите площадь полученной области допустимых значений.
\( \begin{cases} 2^x\cdot 4^y\leq 64\\ 3^x\cdot 81^y\geq 3^{10}\\ x\geq 1 \end{cases} \) $$ \begin{cases} 2^x\cdot 2^{2y}\leq 2^6\\ 3^x\cdot 3^{4y}\geq 3^{10}\\ x\geq 1 \end{cases} \Rightarrow \begin{cases} 2^{x+2y}\leq 2^6\\ 3^{x+4y}\geq 3^{10}\\ x\geq 1 \end{cases} \Rightarrow \begin{cases} x+2y\leq 6\\ x+4y\geq 10\\ x\geq 1 \end{cases} \Rightarrow \begin{cases} -x-2y\geq -6\\ x+4y\geq 10\\ x\geq 1 \end{cases} $$ Сумма первого и второго неравенств с одним знаком сохраняет неравенство:
\(2y\geq 4\Rightarrow y\geq 2\). Перепишем первое неравенство как \(y\leq -\frac12 x+6.\)
Получаем: \( \begin{cases} y\leq-\frac12 x+6\\ y\geq 2\\ x\geq 1 \end{cases} \)
Решаем графически: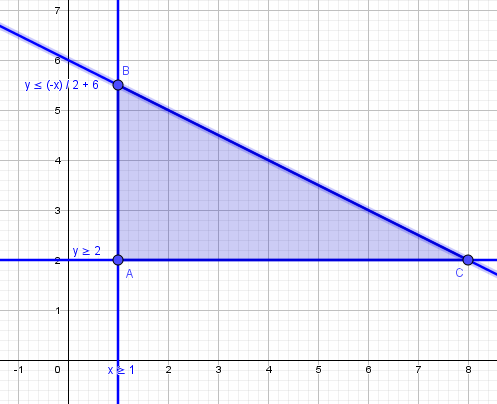
Область допустимых значений – треугольник ABC.
Его площадь: \(S=\frac12 AC\cdot AB=\frac12\cdot(8-1)\cdot(5,5-2)=12,25\)
Ответ: 12,25


