Определение, физический и геометрический смысл производной
п.1. Приращение аргумента и приращение функции
Приращением функции называют соответствующую разность $$ \triangle y=f(x)-f(x_0 )=f(x_0+\triangle x)-f(x_0) $$ Приращение функции может быть как положительным, так и отрицательным.
Например:
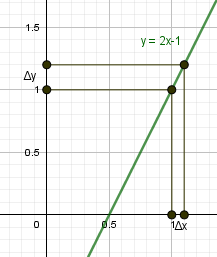 |
\begin{gather*} y=2x-1\\ x_0=1,\ x=1,1 \end{gather*} Найдем приращение аргумента и функции. \begin{gather*} \triangle x= x-x_0=1,1-1=0,1\gt 0\\ \\ f(x)=f(1,1)=2\cdot 1,1-1=1,2\\ f(x_0 )=f(1)=2\cdot 1-1=1\\ \triangle y=f(x)-f(x_0 )=1,2-1=0,2\gt 0 \end{gather*} |
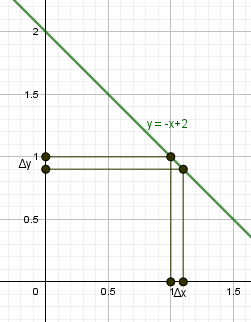 |
\begin{gather*} y=-x+2\\ x_0=1,\ x=1,1 \end{gather*} Найдем приращение аргумента и функции. \begin{gather*} \triangle x= x-x_0=1,1-1=0,1\gt 0\\ \\ f(x)=f(1,1)=-1,1+2=0,9\\ f(x_0 )=f(1)=-1+2=1\\ \triangle y=f(x)-f(x_0)=0,9-1=-0,1\lt 0 \end{gather*} |
п.2. Определение производной
Например:
Найдем производную функции \(f(x)=x^2-4\) в точке \(x_0=3\)
Значение функции в точке: \(f(x_0 )=3^2-4=5\)
Пусть \(\triangle x\) - некоторое приращение аргумента. Тогда: \begin{gather*} f(x)=f(x_0+\triangle x)=(x_0+\triangle x)^2-4=(3+\triangle x)^2-4=9+6\triangle x+\triangle x^2-4=\\ =5+6\triangle x+\triangle x^2 \end{gather*} Приращение функции: $$ \triangle y=f(x)-f(x_0)=5+6\triangle x+\triangle x^2-5=6\triangle x+\triangle x^2=\triangle x(6+\triangle x) $$ Производная: $$ f'(x_0)=\lim_{\triangle x\rightarrow 0}\frac{\triangle x}{\triangle y}=\lim_{\triangle x\rightarrow 0}\frac{\triangle x(6+\triangle x)}{\triangle x}=\lim_{\triangle x\rightarrow 0}(6+\triangle x)=6+0=6 $$ Ответ: 6
п.3. Физический смысл производной
Рассмотрим прямолинейное движение.
Пусть расстояние по прямой между городами \(\triangle x=\) 300 км поезд преодолевает за \(\triangle t=\)4 часа. Мы легко можем найти его среднюю скорость: $$ v_{cp}=\frac{\triangle x}{\triangle t},\ \ v_{cp}=\frac{300}{4}=75\ (\text{км/ч}) $$ Но поезд не едет все время с одной и той же скоростью: где-то ускоряется, где-то замедляется, где-то и вовсе останавливается.
Если мы захотим определить скорость как можно точнее, нам понадобится уменьшать интервалы времени и измерять соответствующий путь. Уменьшив время до «мгновений», мы получим «мгновенную скорость» для каждой точки траектории в каждый момент времени.
Мгновенная скорость равна первой производной от уравнения движения при \(t=t_0\).
Сравнивая определения мгновенной скорости и производной функции, мы можем сформулировать физический смысл производной:
Или, ближе к физике/химии/биологии:
п.4. Геометрический смысл производной
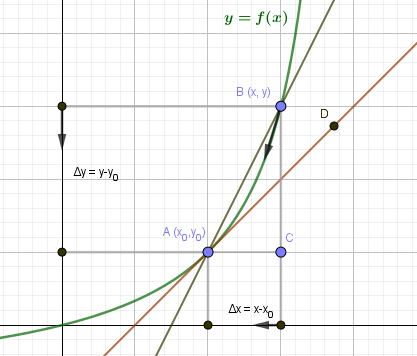
Пусть на плоскости задана кривая \(y=f(x)\).
Выберем на кривой две точки \(A(x_0,y_0)\) и \(B(x,y)\). Прямая AB будет секущей для кривой \(y=f(x)\). Угол наклона прямой AB определяется угловым коэффициентом: $$ k_{AB}=tg\angle A=\frac{BC}{AC}=\frac{\triangle y}{\triangle x} $$ Начнем движение точки B вдоль кривой по направлению к точке A. Приращение аргумента при этом будет уменьшаться: \(\triangle x=AC\rightarrow 0\). В тот момент, когда B совпадет с A, секущая AB превратится в касательную AD. Угловой коэффициент касательной: $$ k_{AD}=\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=y'(x_0) $$
Мы можем сформулировать геометрический смысл производной:
п.5. Алгоритм поиска значения производной в заданной точке
На входе: уравнение функции \(y=f(x)\), точка \(x_0\)
Шаг 1. Найти значение функции в заданной точке \(y_0=f(x_0)\).
Шаг 2. Задать приращение аргумента \(\triangle x=x-x_0\), найти приращение функции \(\triangle y=f(x)-f(x_0)=f(x_0+\triangle x)-f(x_0)\).
Шаг 3. Найти предел \(\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=f'(x_0)\)
На выходе: значение производной в точке \(x_0\)
Например:
Найдем значение производной в точке \(x_0=1\) для функции \(y=x^2-3\).
Значение функции в заданной точке: \(f(x_0)=1^2-3=-2\)
Пусть \(∆x\) - некоторое приращение аргумента. Тогда приращение функции: \begin{gather*} \triangle y=f(x_0+\triangle x)-f(x_0)=((1+\triangle x)^2-3)-(-2)=\\ =1+2\triangle x+(\triangle x)^2-1=2\triangle x+(\triangle x)^2=\triangle x(2+\triangle x) \end{gather*} Ищем предел: \begin{gather*} \lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{\triangle x(2+\triangle x)}{\triangle x}=\lim_{\triangle x\rightarrow 0}(2+\triangle x)=2+0=2 \end{gather*} Искомая производная в заданной точке: \(f'(1)=2\)
Ответ: 2
п.6. Алгоритм поиска уравнения производной
На входе: уравнение функции \(y=f(x)\)
Шаг 1. Задать приращение аргумента \(\triangle x\), найти выражение для приращения функции \(\triangle y=f(x+\triangle x)-f(x)\).
Шаг 2. Найти предел выражения \(\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=f'(x)\)
На выходе: уравнение производной \(y\ '=f'(x)\) в любой точке \(x\).
Например:
Найдем общее уравнение производной для функции \(y=x^2-3\).
Пусть \(∆x\) - некоторое приращение аргумента. Тогда приращение функции: \begin{gather*} \triangle y=f(x+\triangle x)-f(x)=((x+\triangle x)^2-3)-(x^2-3)=\\ =(x+\triangle x)^2-x^2=(x+\triangle x-x)(x+\triangle x+x)=\triangle x(2x+\triangle x) \end{gather*} Ищем предел: \begin{gather*} \lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{\triangle x(2x+\triangle x)}{\triangle x}=\lim_{\triangle x\rightarrow 0}(2x+\triangle x)=2x+0=2x \end{gather*} Ответ: уравнение производной \(y\ '=2x\)
п.7. Примеры
Пример 1. Пользуясь алгоритмом поиска значения производной в заданной точке, найдите:
a) \( f'(1),\ \text{если}\ f(x)=2x \)
По условию \(x_0=1\)
Значение функции в заданной точке: \(f(x_0 )=2\cdot 1=2\)
Пусть \(\triangle x\) - некоторое приращение аргумента. Тогда приращение функции: \begin{gather*} \triangle y=f(x_0+\triangle x)-f(x_0)=2(1+\triangle x)-2=2+2\triangle x-2=2\triangle x \end{gather*} Ищем предел: \begin{gather*} \lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{2\triangle x}{\triangle x}=2 \end{gather*} Искомая производная в заданной точке: \(f'(1)=2\)
б) \( f'(3),\ \text{если}\ f(x)=3x^2 \)
По условию \(x_0=3\)
Значение функции в заданной точке: \(f(x_0 )=3\cdot 3^2=27\)
Пусть \(\triangle x\) - некоторое приращение аргумента. Тогда приращение функции: \begin{gather*} \triangle y=f(x_0+\triangle x)-f(x_0)=3(3+\triangle x)^2-27=3(9+6\triangle x+(\triangle x)^2)-27=\\ =27+18\triangle x+3(\triangle x)^2-27=3\triangle x(6+\triangle x) \end{gather*} Ищем предел: \begin{gather*} \lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{3\triangle x(6+\triangle x)}{\triangle x}=3\lim_{\triangle x\rightarrow 0}(6+\triangle x)=3(6+0)=18 \end{gather*} Искомая производная в заданной точке: \(f'(3)=18\)
в) \( f'(-1),\ \text{если}\ f(x)=4x-1 \)
По условию \(x_0=-1\)
Значение функции в заданной точке: \(f(x_0)=4\cdot (-1)-1=-5\)
Пусть \(\triangle x\) - некоторое приращение аргумента. Тогда приращение функции: \begin{gather*} \triangle y=f(x_0+\triangle x)-f(x_0)=(4(-1+\triangle x)-1)-(-5)=-5+4\triangle x+5=4\triangle x \end{gather*} Ищем предел: \begin{gather*} \lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{4\triangle x}{\triangle x}=4 \end{gather*} Искомая производная в заданной точке: \(f'(-1)=4\)
г) \( f'(2),\ \text{если}\ f(x)=x^3 \)
По условию \(x_0=2\)
Значение функции в заданной точке: \(f(x_0)=2^3=8\)
Пусть \(\triangle x\) - некоторое приращение аргумента. Тогда приращение функции: \begin{gather*} \triangle y=f(x_0+\triangle x)-f(x_0)=(2+\triangle x)^3-8=\\ =2^3+3\cdot 2^2\cdot \triangle x+3\cdot 2\cdot (\triangle x)^2+(\triangle x)^3-8=\\ =12\triangle x+6(\triangle x)^2+(\triangle x)^3=\triangle x\cdot (12+6\triangle x+(\triangle x)^2 ) \end{gather*} Ищем предел: \begin{gather*} \lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{\triangle x\cdot(12+6\triangle x+(\triangle x)^2)}{\triangle x}=\lim_{\triangle x\rightarrow 0}(12+6\triangle x+(\triangle x)^2)=12+0+0=12 \end{gather*} Искомая производная в заданной точке: \(f'(2)=12\)
Ответ: а) 2; б) 18; в) 4; г) 12
Пример 2. Пользуясь алгоритмом поиска уравнения производной, найдите общее уравнение производной для функции \(y=f(x)\):
a) \( f(x)=C\), где C – постоянная величина
Пусть \(\triangle x\) - некоторое приращение аргумента. Тогда приращение функции: \begin{gather*} \triangle y=f(x+\triangle x)-f(x)=C-C=0 \end{gather*} Отношение \(\frac{\triangle y}{\triangle x}=\frac{0}{\triangle x}=0\)
Предел \(\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}0=0\)
Производная \(y\ '=C'=0\)
б) \( f(x)=x\)
Пусть \(\triangle x\) - некоторое приращение аргумента. Тогда приращение функции: \begin{gather*} \triangle y=f(x+\triangle x)-f(x)=x+\triangle x-x=\triangle x \end{gather*} Ищем предел: \(\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{\triangle x}{\triangle x}=\lim_{\triangle x\rightarrow 0}1=1\)
Производная \(x\ '=1\)
в) \( f(x)=x^2\)
Пусть \(\triangle x\) - некоторое приращение аргумента. Тогда приращение функции: \begin{gather*} \triangle y=f(x+\triangle x)-f(x)=(x+\triangle x)^2-x^2=(x+\triangle x-x)(x+\triangle x+x)=\triangle x(2x+\triangle x) \end{gather*} Ищем предел: \begin{gather*} \lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{\triangle x(2x+\triangle x)}{\triangle x}=\lim_{\triangle x\rightarrow 0}(2x+\triangle x)=2x+0=2x \end{gather*} Производная \((x^2)\ '=2x\)
г) \( f(x)=x^3\)
Пусть \(\triangle x\) - некоторое приращение аргумента. Тогда приращение функции: \begin{gather*} \triangle y=f(x+\triangle x)-f(x)=(x+\triangle x)^3-x^3=\\ =(x+\triangle x-x)((x+\triangle x)^2+x(x+\triangle x)+x^2)=\triangle x((x+\triangle x)^2+x(x+\triangle x)+x^2) \end{gather*} Ищем предел: \begin{gather*} \lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{\triangle x((x+\triangle x)^2+x(x+\triangle x)+x^2)}{\triangle x}=\\ =\lim_{\triangle x\rightarrow 0}((x+\triangle x)^2+x(x+\triangle x)+x^2)=(x+0)^2+x(x+0)+x^2=3x^2 \end{gather*} Производная \((x^3)\ '=3x^2\)
д) \( f(x)=\frac1x\)
Пусть \(\triangle x\) - некоторое приращение аргумента. Тогда приращение функции: \begin{gather*} \triangle y=f(x+\triangle x)-f(x)=\frac{1}{x+\triangle x}-\frac1x=\frac{x-(x+\triangle x)}{x(x+\triangle x)}=-\frac{\triangle x}{x(x+\triangle x)} \end{gather*} Ищем предел: \begin{gather*} \lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\left(-\frac{\triangle x}{\triangle x\cdot x(x+\triangle x)}\right)=-\lim_{\triangle x\rightarrow 0}\frac{1}{x(x+\triangle x)}=-\frac{1}{x(x+0)}=-\frac{1}{x^2} \end{gather*} Производная \(\left(\frac1x\right)\ '=-\frac{1}{x^2}\)
e) \( f(x)=kx+b\)
Пусть \(\triangle x\) - некоторое приращение аргумента. Тогда приращение функции: \begin{gather*} \triangle y=f(x+\triangle x)-f(x)=k(x+\triangle x)+b-kx-b=k\triangle x \end{gather*} Ищем предел: \begin{gather*} \lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{k\triangle x}{\triangle x}=\lim_{\triangle x\rightarrow 0}k=k \end{gather*} Производная \((kx+b)\ '=k\)
ж) \( f(x)=\sqrt{x}\)
Пусть \(\triangle x\) - некоторое приращение аргумента. Тогда приращение функции: \begin{gather*} \triangle y=f(x+\triangle x)-f(x)=\sqrt{x+\triangle x}-\sqrt{x} \end{gather*} Ищем предел, умножив числитель и знаменатель на сопряженное выражение: \begin{gather*} \lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{\sqrt{x+\triangle x}-\sqrt{x}}{\triangle x}= \lim_{\triangle x\rightarrow 0}\frac{(\sqrt{x+\triangle x}-\sqrt{x})(\sqrt{x+\triangle x}+\sqrt{x})}{\triangle x(\sqrt{x+\triangle x}+\sqrt{x})}=\\ =\lim_{\triangle x\rightarrow 0}\frac{x+\triangle x-x}{\triangle x(\sqrt{x+\triangle x}+\sqrt{x})}=\lim_{\triangle x\rightarrow 0}\frac{1}{(\sqrt{x+\triangle x}+\sqrt{x})}=\frac{1}{\sqrt{x+0}+\sqrt{x}}=\frac{1}{2\sqrt{x}} \end{gather*} Производная \((\sqrt{x})\ '=\frac{1}{2\sqrt{x}}\)


