Исследование функции на монотонность и экстремумы, выпуклость и точки перегиба
п.1. Производная функции и промежутки монотонности
Рассмотрим кусочно-непрерывную функцию: \( y= \begin{cases} x+1,\ \ x\leq 1\\ 2,\ \ 1\lt x\leq 4\\ 6-x,\ \ x\gt 4 \end{cases} \)
Эта функция интересна тем, что имеет промежуток возрастания при \(x\leq 1\), промежуток постоянства при \(1\lt x\leq 4\) и промежуток убывания при \(x\gt 4\).
Посмотрим, как ведет себя производная на каждом из промежутков, используя определение производной (см. §42 данного справочника).
Заметим, что в точках излома x=1 и x=4 функция определена и непрерывна, но её производная не существует.
При \(x\lt 1\): $$ \triangle y=(f(x_0+\triangle x)-f(x_0)=\left((x_0+\triangle x)+1\right)-(x_0+1)=\triangle x $$ Получается, что знаки \(\triangle y\) и \(\triangle x\) всегда совпадают, и их частное \(\frac{\triangle y}{\triangle x}=1\gt 0\) - всегда положительно. Поэтому и производная на промежутке возрастания функции положительна: $$ f'(x_0)=\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{\triangle x}{\triangle x}=\lim_{\triangle x\rightarrow 0}1=1\gt 0 $$ При \(1\lt x\lt 4\): $$ \triangle y=f(x_0+\triangle x)-f(x_0)=2-2=0 $$ Производная на промежутке постоянства равна нулю: $$ f'(x_0)=\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{0}{\triangle x}=\lim_{\triangle x\rightarrow 0}0=0 $$ При \(x\gt 4\): $$ \triangle y=f(x_0+\triangle x)-f(x_0)=\left(6-(x_0+\triangle x)\right)-(6-x_0)=-\triangle x $$ Знаки \(\triangle y\) и \(\triangle x\) всегда противоположны, и их частное \(\frac{\triangle y}{\triangle x}=-1\lt 0\) - всегда отрицательны. Поэтому и производная на промежутке убывания функции отрицательна: $$ f'(x_0)=\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{-\triangle x}{\triangle x}=\lim_{\triangle x\rightarrow 0}(-1)=-1\lt 0 $$ Полученные результаты можно обобщить для любой функции, поскольку всегда:
- на промежутках возрастания \(\frac{\triangle y}{\triangle x}\gt 0\) и \(f'(x)\gt 0,\)
- на промежутках постоянства \(\frac{\triangle y}{\triangle x}=0\) и \(f'(x)=0,\)
- на промежутках убывания \(\frac{\triangle y}{\triangle x}\lt 0\) и \(f'(x)\lt 0,\)
Верно и обратное утверждение:
Если в каждой точке некоторого промежутка производная функции \(y=f(x)\):
- положительна, то функция на этом промежутке возрастает;
- равна нулю, то функция на этом промежутке постоянна;
- отрицательна, то функция на этом промежутке убывает.
п.2. Критические точки
Например:
Найдем критические точки функции \(y=\frac{x^2-10x+16}{x^2}\)
Точка \(x=0\notin D\) не входит в ОДЗ функции, следовательно, производная в ней не существует и \(x=0\) – критическая точка.
Найдем точки, в которых производная равна 0.
Преобразуем выражение: \(\frac{x^2-10x+16}{x^2}=1-\frac{10}{x}+\frac{16}{x^2}\) \begin{gather*} y'=\left(1-\frac{10}{x}+\frac{16}{x^2}\right)=0+\frac{10}{x^2}-\frac{16\cdot 2}{x^3}=\frac{10x-32}{x^3}=\frac{10(x-3,2)}{x^3}\\ y'=0\ \text{при}\ x=3,2 \end{gather*} Ответ: x=0 и x=3,2
Напомним, что:
Точка \(x_0\) является точкой максимума функции \(y=f(x)\), если для всех \(x(x\ne x_0)\) из некоторой окрестности точки \(x_0\) выполняется неравенство \(f(x_0 )\gt f(x)\).
Все точки минимума и максимума функции \(y=f(x)\) образуют множество точек экстремума данной функции.
| Необходимое условие существования экстремума Точками экстремума функции могут быть только её критические точки. |
Т.е. все критические точки объявляются подозрительными на экстремум.
| Достаточное условие существования экстремума Точка \(x_0\) принадлежит промежутку непрерывности функции \(y=f(x)\) и при подходе к точке \(x_0\) слева и справа производные имеют разные знаки. |
Т.е., для всех точек, подозрительных на экстремум, которые лежат в промежутках непрерывности функции и для которых производные слева и справа имеют разные знаки, «подозрение подтверждается» - и такие точки признаются экстремумами.
Например:
Исследуем промежутки монотонности и найдем экстремумы функции \(y=\frac{x^2-10x+16}{x^2}\).
Выше мы уже нашли критические точки: \(x=0\) и \(x=3,2\).
Производная: \(y'=\frac{10(x-3,2}{x^3}\)
Определить знак производной на промежутке просто: нужно взять любое значение x из промежутка и подставить в производную. При этом не нужно точно считать, сколько получается; главное – понять, какой знак у каждой скобки/множителя.
Составим таблицу:
| \(x\) | \((-\infty;0)\) | 0 | (0;3,2) | 3,2 | \((3,2;+\infty)\) |
| \(f'(x)\) | >0 | не существует | <0 | 0 | >0 |
| \(f(x)\) | \(\nearrow\) | не существует | \(\searrow\) | min | \(\nearrow\) |
Вывод:
Функция возрастает при \(x\in(-\infty;0)\cup(3,2;+\infty)\)
Функция убывает при \(x\in(0;3,2)\)
Точка минимума \(x=3,2; y_{min}=f(3,2)=-\frac{9}{16}\)
п.3. Вторая производная, промежутки выпуклости и точки перегиба
Пусть функция \(y=f(x)\) является дифференцируемой на промежутке \(x\in(a;b)\), и её производная \(f'(x)\) также является дифференцируемой на этом же промежутке.
Тогда существует производная от производной: \(\left(f'(x)\right)'=f''(x)\), которую называют второй производной или производной второго порядка от функции \(y=f(x)\).
Например:
1) Найдем вторую производную для \(y=3x^4+2x^3+4x\)
\(f'(x)=3\cdot 4x+2\cdot 3x^2+4\cdot 1=12x^3+6x^2+4\)
\(f''(x)=12\cdot 3x^2+6\cdot 2x+0=36x^2+12x\)
2) Найдем вторую производную для \(y=\frac{x^2-10x+16}{x^2}\).
Первую мы уже нашли выше: \(f'(x)=\frac{10(x-3,2)}{x^3}=\frac{10}{x^2}-\frac{32}{x^3}\)
Получаем: \(f''(x)=\left(\frac{10}{32}-\frac{32}{x^3}\right)'=-\frac{10\cdot 2}{x^3}+\frac{32\cdot 3}{x^4}=\frac{-20x+96}{x^4}=-\frac{20(x-4,8)}{x^4}\)
Кривая \(y=f(x)\) называется выпуклой вниз на интервале \((a;b)\), если все точки, кроме точки касания \(x_0\), лежат над касательной, проведенной через любую точку \(x_0\in(a;b)\).
Точка кривой \(y=f(x)\), в которой меняется характер выпуклости, называется точкой перегиба.
Например:
 |
Точка A принадлежит промежутку, выпуклому вверх, т.к. все точки этого промежутка лежат под касательной, проведенной через A. Точка B принадлежит промежутку, выпуклому вниз, т.к. все точки этого промежутка лежат над касательной, проведенной через B. Точка C - точка перегиба. |
Если в каждой точке некоторого промежутка (a;b) вторая производная функции \(y=f(x)\):
|
| Необходимое условие существования точки перегиба Точками перегиба функции могут быть только её критические точки второго порядка. |
Т.е. все критические точки второго порядка объявляются подозрительными на перегиб.
| Достаточное условие существования точки перегиба Точка \(x_0\) принадлежит промежутку непрерывности первой производной \(f'(x)\) и при подходе к точке \(x_0\) слева и справа вторые производные имеют разные знаки. |
Т.е., для всех точек, подозрительных на перегиб, которые лежат в промежутках непрерывности первой производной и для которых вторые производные слева и справа имеют разные знаки, «подозрение подтверждается» - и такие точки признаются точками перегиба.
Например:
Продолжим исследование функции \(y=\frac{x^2-10x+16}{x^2}\) и найдем промежутки выпуклости и точки перегиба.
Вторая производная: \(f''(x)=\frac{-20(x-4,8)}{x^4}\)
Критические точки второго порядка: \(x=0\) и \(x=4,8\).
Составим таблицу:
| \(x\) | \((-\infty;0)\) | 0 | (0;4,8) | 4,8 | \((4,8;+\infty)\) |
| \(f''(x)\) | >0 | не существует | >0 | 0 | <0 |
| \(f(x)\) | \(\cup\) | не существует | \(\cup\) | перегиб | \(\cap\) |
Вывод:
Функция выпуклая вниз при \(x\in(-\infty;0)\cup(0;4,8)\)
Функция выпуклая вверх при \(x\in(4,8;+\infty)\)
Точка перегиба \(x=4,8;\ f(4,8)=\frac{7}{18}\)
п.4. Примеры
Пример 1. Найдите промежутки монотонности и точки экстремума функции:
a) \( y=2x^3-6x^2-18x+7 \)
ОДЗ: \(x\in\mathbb{R}\)
Первая производная: \begin{gather*} f'(x)=2\cdot 3x^2-6\cdot 2x-18\cdot 1+0=6x^2-12x-18=6(x^2-2x-3)=\\ =6(x-3)(x+1)\\ f'(x)=0\ \text{при} \left[ \begin{array}{l} x=3\\ x=-1 \end{array} \right. \end{gather*} Критические точки: \(x=-1\) и \(x=3\)
Составляем таблицу:
| \(x\) | \((-\infty;-1)\) | -1 | (-1;3) | 3 | \((3;+\infty)\) |
| \(f'(x)\) | >0 | 0 | <0 | 0 | >0 |
| \(f(x)\) | \(\nearrow\) | max | \(\searrow\) | min | \(\nearrow\) |
Вывод:
Функция возрастает при \(x\in(-\infty;-1)\cup(3;+\infty)\)
Функция убывает при \(x\in(-1;3)\)
Точка максимума \(x=-1;\ y_{max}=f(-1)=-2-6+18+7=17\)
Точка минимума \(x=3;\ y_{min}=f(3)=54-54-54+7=-47\)
б) \( y=\frac{x^2}{x^2-9} \)
ОДЗ: \(x^2-9=ne 0\Rightarrow x\ne\pm 3\)
Первая производная: \begin{gather*} f'(x)=\frac{2x(x^2-9)-x^2\cdot 2x}{(x^2-9)^2}=\frac{2x(x^2-9-x^2)}{(x^2-9)^2}=-\frac{18x}{(x^2-9)^2} \end{gather*} Критические точки: \(x=\left\{0;\pm 3\right\}\)
Составляем таблицу:
| \(x\) | \((-\infty;-3)\) | -3 | (-3;0) | 0 | \((0;3)\) | 3 | \((3+\infty)\) |
| \(f'(x)\) | >0 | не существует | >0 | 0 | <0 | не существует | <0 |
| \(f(x)\) | \(\nearrow\) | не существует | \(\nearrow\) | max | \(\searrow\) | не существует | \(\searrow\) |
Вывод:
Функция возрастает при \(x\in(-\infty;-3)\cup(-3;0)\)
Функция убывает при \(x\in(0;3)\cup(3;+\infty)\)
Точка максимума \(x=0;\ y_{max}=f(0)=0\)
в) \( y=\frac3x+\frac x3 \)
ОДЗ: \(x\ne 0\)
Первая производная: \begin{gather*} f'(x)=-\frac{3}{x^2}+\frac13=\frac{x^2-9}{3x^2}=\frac{(x+3)(x-3)}{3x^2}\\ f'(x)=0\ \text{при}\ x=\pm 3 \end{gather*} Критические точки: \(x=\left\{0;\pm 3\right\}\)
Составляем таблицу:
| \(x\) | \((-\infty;-3)\) | -3 | (-3;0) | 0 | \((0;3)\) | 3 | \((3+\infty)\) |
| \(f'(x)\) | >0 | 0 | <0 | \(\varnothing\) | <0 | 0 | >0 |
| \(f(x)\) | \(\nearrow\) | max | \(\searrow\) | \(\varnothing\) | \(\searrow\) | min | \(\nearrow\) |
Вывод:
Функция возрастает при \(x\in(-\infty;-3)\cup(-3;+\infty)\)
Функция убывает при \(x\in(-3;0)\cup(0;3)\)
Точка максимума \(x=-3;\ y_{max}=f(-3)=-1-1=-2\)
Точка минимума \(x=3;\ y_{min}=f(3)=1+1=2\)
г*) \( y=\frac{x^2}{8}-\ln(x^2-8) \)
ОДЗ: \(x^2-8\gt 0\Rightarrow x^2\gt 8\Rightarrow |x|\gt \sqrt{8}\Rightarrow x\lt -2\sqrt{2}\cup x\gt 2\sqrt{2}\)
Критические точки на границе ОДЗ: \(x=\pm 2\sqrt{2}\)
Первая производная: \begin{gather*} f'(x)=\frac{2x}{8}-\frac{2x}{x^2-8}=2x\left(\frac18-\frac{1}{x^2-8}\right)=\frac{2x(x^2-8-8)}{8(x^2-8)}=\frac{x(x^2-16)}{4(x^2-8)}=\\ =\frac{x(x+4)(x-4)}{4(x+2\sqrt{2})(x-2\sqrt{2})}\\ f'(x)=0\ \text{при}\ x=\left\{0;\pm 4\right\} \end{gather*} \(x=0\notin D\) – не входит в ОДЗ.
Критические точки: \(x=\left\{\pm2\sqrt{2};\pm 4\right\}\)
Составляем таблицу:
| \(x\) | \((-\infty;-4)\) | -4 | \((-4;-2\sqrt{2})\) | \(-2\sqrt{2}\) | \((-2\sqrt{2};2\sqrt{2})\) | \(2\sqrt{2}\) | \((2\sqrt{2};4)\) | 4 | \((4;+\infty)\) |
| \(f'(x)\) | <0 | 0 | >0 | \(\varnothing\) | \(\varnothing\) | \(\varnothing\) | <0 | 0 | >0 |
| \(f(x)\) | \(\searrow\) | min | \(\nearrow\) | \(\varnothing\) | \(\varnothing\) | \(\varnothing\) | \(\searrow\) | min | \(\nearrow\) |
Вывод:
Функция возрастает при \(x\in(-4;-2\sqrt{2})\cup(4;+\infty)\)
Функция убывает при \(x\in(-\infty;-4)\cup(2\sqrt{2};4)\)
Точка минимума $$ x=\pm 4;\ y_{min}=f(\pm 4)=\frac{16}{8}-\ln(16-8)=2-\ln 8=2-\ln 2^3=2-3\ln 2 $$
Пример 2. Найдите промежутки выпуклости и точки перегиба функции:
a) \( y=2x^3-6x^2-18x+7 \)
Первая производная: \begin{gather*} f'(x)=2\cdot 3x^2-6\cdot 2x-18\cdot 1+0=6x^2-12x-18 \end{gather*} Вторая производная: \begin{gather*} f''(x)=6\cdot 2x-12\cdot 1-0=12x-12=12(x-1)\\ f''(x)=0\ \text{при}\ x=1 \end{gather*} Критическая точка 2-го порядка: \(x=1\)
Составляем таблицу:
| \(x\) | \((-\infty;1)\) | 1 | \((1;+\infty)\) |
| \(f''(x)\) | <0 | 0 | >0 |
| \(f(x)\) | \(\cap\) | перегиб | \(\cup\) |
Вывод:
Функция выпуклая вверх при \(x\in(-\infty;1)\)
Функция выпуклая вниз при \(x\in(1;+\infty)\)
Точка перегиба \(x=1;\ f(1)=2-6-18+7=-15\)
б) \( y=\frac{x^2}{x^2-9} \)
ОДЗ: \(x^2-9\ne 0\Rightarrow x\ne \pm 3\)
Первая производная: \begin{gather*} f'(x)=\frac{2x(x^2-9)-x^2\cdot 2x}{(x^2-9)^2}=\frac{2x(x^2-9-x^2)}{(x^2-9)^2}=-\frac{18x}{(x^2-9)^2} \end{gather*} Вторая производная: \begin{gather*} f''(x)=-18\left(\frac{1\cdot (x^2-9)^2-x\cdot 2(x^2-9)\cdot 2x}{(x^2-9)^4}\right)=-18\left(\frac{(x^2-9)-4x^2}{(x^2-9)^3}\right)=\\ =-28\left(\frac{-3x^2-9}{(x^2-9)^3}\right)=\frac{54(x^2+3)}{(x^2-9)^3} \end{gather*} \( f''(x)=0\ \text{при}\ x=\in\varnothing\) - таких x нет.
Критические точки 2-го порядка: \(x=\left\{\pm 3\right\}\)
Составляем таблицу:
| \(x\) | \((-\infty;-3)\) | -3 | \((-3;3)\) | 3 | \((3;+\infty)\) |
| \(f''(x)\) | >0 | не существует | <0 | не существует | >0 |
| \(f(x)\) | \(\cup\) | не существует | \(\cap\) | не существует | \(\cup\) |
Вывод:
Функция выпуклая вверх при \(x\in(-3;3)\)
Функция выпуклая вниз при \(x\in(-\infty;-3)\cup(3;+\infty)\)
Точек перегиба нет.
в) \( y=\frac3x+\frac x3 \)
ОДЗ: \(x\ne 0\)
Первая производная: \begin{gather*} f'(x)= -\frac{3}{x^2}+\frac13=\frac{x^2-9}{3x^2} \end{gather*} Вторая производная: \begin{gather*} f''(x)=\frac13\left(1-\frac{9}{x^2}\right)'=\frac13\left(0+\frac{9\cdot 2}{x^3}\right)=\frac{6}{x^3} \end{gather*} Вторая производная нулей не имеет.
Критическая точка 2-го порядка: \(x=0\)
Составляем таблицу:
| \(x\) | \((-\infty;0)\) | 0 | \((0;+\infty)\) |
| \(f''(x)\) | <0 | \(\varnothing\) | >0 |
| \(f(x)\) | \(\cap\) | \(\varnothing\) | \(\cup\) |
Вывод:
Функция выпуклая вверх при \(x\in(-\infty;0)\)
Функция выпуклая вниз при \(x\in(0;+\infty)\)
Точек перегиба нет.
г*) \( y=\frac{x^2}{8}-\ln(x^2-8) \)
ОДЗ: \(x^2-8\gt 0\Rightarrow x^2\gt 8\Rightarrow |x|\gt \sqrt{8}\Rightarrow x\lt -2\sqrt{2}\cup x\gt 2\sqrt{2}\)
Критические точки на границе ОДЗ: \(x=\pm 2\sqrt{2}\)
Первая производная: \begin{gather*} f'(x)=\frac{2x}{8}-\frac{2x}{x^2-8}=2x\left(\frac18-\frac{1}{x^2-8}\right)=\frac{2x(x^2-8-8)}{8(x^2-8)}=\frac{x(x^2-16)}{4(x^2-8)} \end{gather*} Вторая производная: \begin{gather*} f''(x)=\frac14\left(\frac{x^3-16x}{x^2-8}\right)'=\frac14\cdot\frac{(3x^2-16)(x^2-8)-(x^3-16x)\cdot 2x}{(x^2-8)^2}=\\ =\frac14\cdot\frac{3x^4-40x^2+128-2x^4+32x^2}{(x^2-8)^2}=\frac14\cdot\frac{x^4-8x^2+128}{(x^2-8)^2} \end{gather*} Для биквадратного уравнения \(x^4-8x^2+128=0\) дискриминант \(D=64-4\cdot 128\lt 0\)
Значит, \(x^4-8x^2+128\gt 0\) на всей ОДЗ. Нулей у второй производной нет.
Критические точки 2-го порядка: \(x=\left\{\pm 2\sqrt{2}\right\}\)
Составляем таблицу:
| \(x\) | \((-\infty;-2\sqrt{2})\) | \(-2\sqrt{2} \) | \((-2\sqrt{2};2\sqrt{2})\) | \(2\sqrt{2}\) | \((2\sqrt{2};+\infty)\) |
| \(f''(x)\) | >0 | \(\varnothing\) | \(\varnothing\) | \(\varnothing\) | >0 |
| \(f(x)\) | \(\cup\) | \(\varnothing\) | \(\varnothing\) | \(\varnothing\) | \(\cup\) |
Вывод:
Функция выпуклая вниз при \(x\in(-\infty;-2\sqrt{2})\cup(2\sqrt{2};+\infty)\) (на всей ОДЗ)
Точек перегиба нет.
Пример 3*. Найдите наименьшее значение функции:
\begin{gather*} y=3^x+2\cdot 3^{3-x}-x\ln 27-9 \end{gather*} ОДЗ: \(x\in\mathbb{R}\)
Первая производная: \begin{gather*} f'(x)=3^x\ln 3+2\cdot 3^{3-x}\cdot (3-x)'\cdot \ln 3-1\cdot\ln 27-0=\\ =3^x\ln 3-2\cdot 3^{3-x}\ln 3-\ln 3^3=3^x\ln 3-2\cdot 3^3\cdot 3^{-x}\ln 3-3\ln 3=\\ =\ln 3\cdot (3^x-54\cdot 3^{-x}-3) \end{gather*} Найдём нули первой производной: \begin{gather*} \ln 3\cdot (3^x-54\cdot 3^{-x}-3)=0\ |:\ln 3\\ 3^x-54\cdot 3^{-x}-3=0 \end{gather*} Замена: \(t=3^x\gt 0\) \begin{gather*} t-\frac{54}{t}-3=0\Rightarrow \frac{t^2-3t-54}{t}=0\Rightarrow \begin{cases} t^2-3t-54=0\\ t\ne 0 \end{cases} \\ (t+6)(t-9)=0\Rightarrow \left[ \begin{array}{l} t=-6\lt 0 -\ \text{не подходит}\\ t=9 \end{array} \right. \end{gather*} Возвращаемся к исходной переменной: \(3^x=9\Rightarrow x=2\) $$ f'(x)=0\ \text{при}\ x=2 $$ Критическая точка \(x=2\)
Для определения знаков в промежутке \((-\infty;2)\) можно взять \(x=1\) и тогда:
$$ f'(1)=\ln 3\cdot (3^1-54\cdot 3^{-1}-3)=\ln 3\cdot (3-18-3)\lt 0 $$ В промежутке \((2;+\infty)\) можно взять 3 и тогда: $$ f'(3)=\ln 3\cdot (3^3-54\cdot 3^{-3}-3)=\ln 3\cdot (27-2-3)\gt 0 $$ Получаем:
| \(x\) | \((-\infty;2)\) | 2 | \((2;+\infty)\) |
| \(f'(x)\) | <0 | 0 | >0 |
| \(f(x)\) | \(\searrow\) | min | \(\nearrow\) |
\(x=2\) точка минимума.
Значение функции в этой точке: \begin{gather*} y_{min}=f(2)=3^2+2\cdot 3^{3-2}-2\ln 27-9=9+6-2\ln 3^3-9=\\ =6-6\ln 3=6(1-\ln 3) \end{gather*} Ответ: \(y_{min}=6(1-\ln 3)\) при \(x=2\)
Пример 4*. Найдите наибольшее значение функции \begin{gather*} f(x)=x^4-6bx^2+b^2 \end{gather*} на отрезке [-2;1] в зависимости от параметра b.
Первая производная: \begin{gather*} f'(x)=4x^3-12bx=4x(x^2-3b)\\ f'(x)=0\ \text{при}\ x=0\ \text{и}\ x=\pm\sqrt{3b} \end{gather*}
При \(b\gt 0\ f(x)\) имеет три критических точки $$ x=\left\{0;\pm\sqrt{3b}\right\} $$ 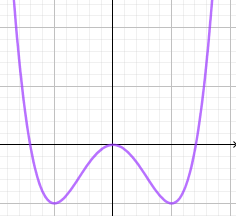 |
При \(b\lt 0\ f(x)\) имеет только минимум в \(x=0\)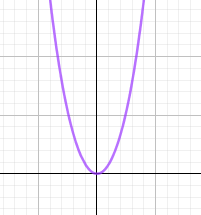 Т.к. функция четная, можно сразу сказать, что максимальное значение на заданном отрезке будет при \(x=-2\). |
Критическая точка \(x=0\) будет при любом b. При \(b\gt 0,\ x=0\) будет максимумом, при \(b\leq 0\) – минимумом.
Пара критических точек \(x=\pm\sqrt{3b}\) появляется только при условии \(b\gt 0\), и это две точки минимума. Т.к. по условию мы ищем точку максимума (наибольшее значение функции), эти точки нам не интересны.
Поэтому рассмотрим значения на концах отрезка и в нуле в общем случае: \begin{gather*} f(-2)=(-2)^4-6b\cdot(-2)^2+b^2=b^2-24b+16\\ f(0)=b^2\\ f(1)=1-6b+b^2 \end{gather*} Сравниваем попарно значения функций: \begin{gather*} f(1)-f(0)=1-6b+b^2-b^2=1-6b\\ f(1)\gt f(0)\ \text{при}\ b\lt\frac16\\ f(1)\lt f(0)\ \text{при}\ b\gt\frac16\\ \\ f(-2)-f(0)=b^2-24b+16-b^2=16-24b=8(2-3b)\\ f(-2)\gt f(0)\ \text{при}\ b\lt\frac23\\ f(-2)\lt f(0)\ \text{при}\ b\gt\frac23\\ \\ f(-2)-f(1)=b^2-24b+16-(1-6b+b^2)=-18b+15=3(5-6b)\\ f(-2)\gt f(1)\ \text{при}\ b\lt\frac56\\ f(-2)\lt f(1)\ \text{при}\ b\gt\frac56\\ \end{gather*} Получаем таблицу:
| b | Соотношение значений функции |
| \(\left(-\infty;\frac16\right)\) | \(f(-2)\gt f(1)\gt f(0)\) |
| \(\frac16\) | \(f(-2)\gt f(1)=f(0)\) |
| \(\left(\frac16;\frac23\right)\) | \(f(-2)\gt f(0)\gt f(1)\) |
| \(\frac23\) | \(f(-2)=f(0)\gt f(1)\) |
| \(\left(\frac23;\frac56\right)\) | \(f(0)\gt f(-2)\gt f(1)\) |
| \(\frac56\) | \(f(0)\gt f(-2)=f(1)\) |
| \(\left(\frac56;+\infty\right)\) | \(f(0)\gt f(1)\gt f(2)\) |
Получаем, что при \(b\lt\frac23\) максимальное значение на отрезке имеет $$ f(-2)=b^2-24b+16 $$ При \(b\geq \frac23\) максимальное значение будет для \(f(0)=b^2\)
Ответ:
При \(b\lt\frac23,\ max_{[-2;1]}f(x)=f(-2)=b^2-24b+16\)
При \(b\geq\frac23,\ max_{[-2;1]}f(x)=f(0)=b^2\)


