Единичная числовая окружность на координатной плоскости

п.1. Понятие тригонометрии

Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., - спроектирован с использованием тригонометрии.

п.2. Числовая окружность

Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.

Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета, ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным; по часовой стрелке – отрицательным.

Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90&deg, –120°, –180°.

п.3. Градусная и радианная мера угла

Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).

В целом, более обоснованной и естественной для измерения углов является радианная мера.

Найдем радианную меру прямого угла ∠AOB=90°. Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr. Длина дуги AB: \(l_{AB}=\frac{L}{4}=\frac{2\pi r}{4}=\frac{\pi r}{2}.\) Тогда радианная мера угла: $$ \angle AOB=\frac{l_{AB}}{r}=\frac{\pi r}{2\cdot r}=\frac{\pi}{2} $$

п.4. Свойства точки на числовой окружности

Построим числовую окружность. Обозначим O(0;0), A(1;0)

Каждому действительному числу t на числовой окружности соответствует точка Μ(t). При t=0, M(0)=A. При t>0 двигаемся по окружности против часовой стрелки, описывая дугу ⌒ AM=t. Точка M - искомая. При t<0 двигаемся по окружности по часовой стрелке, описывая дугу ⌒ AM=t. Точка M - искомая.

Отметим на числовой окружности точки, соответствующие \(\frac{\pi}{6},\ \frac{\pi}{4},\ \frac{\pi}{2},\ \frac{2\pi}{3},\ \pi\), а также \(-\frac{\pi}{6},\ -\frac{\pi}{4},\ -\frac{\pi}{2},\ -\frac{2\pi}{3},\ -\pi\) Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности.

Отметим на числовой окружности точки, соответствующие \(\frac{\pi}{6},\ \frac{13\pi}{6},\ \frac{25\pi}{6}\), и \(-\frac{11\pi}{6}\). Все четыре точки совпадают, т.к. \begin{gather*} M\left(\frac{\pi}{6}\right)=M\left(\frac{\pi}{6}+2\pi k\right)\\ \frac{\pi}{6}-2\pi=-\frac{11\pi}{6}\\ \frac{\pi}{6}+2\pi=\frac{13\pi}{6}\\ \frac{\pi}{6}+4\pi=\frac{25\pi}{6} \end{gather*}

п.5. Интервалы и отрезки на числовой окружности

Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.

Числовой промежуток	Соответствующая дуга числовой окружности
Отрезок
$$ -\frac{\pi}{6} \lt t \lt \frac{\pi}{3} $$ а также, с учетом периода $$ -\frac{\pi}{6}+2\pi k\lt t\lt\frac{\pi}{3}+2\pi k $$
Интервал
$$ -\frac{\pi}{6} \leq t \leq \frac{\pi}{3} $$ а также, с учетом периода $$ -\frac{\pi}{6}+2\pi k\leq t\leq\frac{\pi}{3}+2\pi k $$
Полуинтервал
$$ -\frac{\pi}{6} \leq t \lt\frac{\pi}{3} $$ а также, с учетом периода $$ -\frac{\pi}{6}+2\pi k\leq t\lt\frac{\pi}{3}+2\pi k $$

п.6. Примеры

Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?

Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: \begin{gather*} BE=30^{\circ}=\frac{\pi}{6}.\\ EC=60^{\circ}=\frac{\pi}{3}.\\ AE=EC+CD=90^{\circ}+30^{\circ}=120^{\circ}=\frac{2\pi}{3}.\\ ED=EC+CD=60^{\circ}+90^{\circ}=150^{\circ}=\frac{5\pi}{6}. \end{gather*}

Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: \(-\frac{\pi}{2};\ \frac{3\pi}{4};\ \frac{7\pi}{6};\ \frac{7\pi}{4}\).

Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. \begin{gather*} -\frac{\pi}{2}=-90^{\circ},\ \ \frac{3\pi}{4}=135^{\circ}\\ \frac{7\pi}{6}=210^{\circ},\ \ \frac{7\pi}{4}=315^{\circ} \end{gather*}

Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: \(-\frac{11\pi}{2};\ 5\pi;\ \frac{17\pi}{6};\ \frac{27\pi}{4}\).

Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk - четное количество π), чтобы попасть в промежуток от 0 до 2π. Далее – действуем, как в примере 2. \begin{gather*} -\frac{11\pi}{2}=\frac{-12+1}{2}\cdot\pi=-6\pi+\frac{\pi}{2}\rightarrow \frac{\pi}{2}=90^{\circ}\\ 5\pi=4\pi+\pi\rightarrow \pi=180^{\circ}\\ \frac{17\pi}{6}=\frac{18-1}{6}\pi=3\pi-\frac{\pi}{6}\rightarrow \pi-\frac{\pi}{6}=\frac{5\pi}{6}\\ \frac{27\pi}{4}=\frac{28-1}{4}\pi=7\pi-\frac{\pi}{4}\rightarrow \pi-\frac{\pi}{4}=\frac{3\pi}{4} \end{gather*}

Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.

Сравниваем каждое число с границами четвертей: \begin{gather*} 0,\ \ \frac\pi2\approx\frac{3,14}{2}=1,57,\ \ \pi\approx 3,14\\ 3\pi\ \ 3\cdot 3,14\\ \frac{3\pi}{2}\approx \frac{3\cdot 3,14}{2}=4,71,\ \ 2\pi\approx 6,28 \end{gather*}

\(\frac\pi2\lt 2\lt \pi \Rightarrow \) угол 2 радиана находится во 2-й четверти
\(\pi\lt 4\lt \frac{3\pi}{2} \Rightarrow \) угол 4 радиана находится в 3-й четверти
\(\frac{3\pi}{2}\lt 5\lt 2\pi \Rightarrow \) угол 5 радиана находится в 4-й четверти
\(7\gt 2\pi\), отнимаем полный оборот: \(0\lt 7-2\pi\lt \frac\pi2\Rightarrow\) угол 7 радиан находится в 1-й четверти.

Пример 5. Изобразите на числовой окружности множество точек \((k\in\mathbb{Z})\), запишите количество полученных базовых точек.

$$ \frac{\pi k}{2} $$	$$ -\frac{\pi}{4}+2\pi k $$
Четыре базовых точки, через каждые 90°	Две базовых точки, через каждые 180°
$$ \frac{\pi}{3}+\frac{2\pi k}{3} $$	$$ -\frac{\pi k}{5} $$
Три базовых точки, через каждые 120°	Пять базовых точек, через каждые 72°

Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.

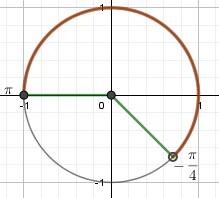
$$ \left[0;\ \frac{\pi}{3}\right] $$	$$ \left(-\frac{\pi}{4};\ \pi\right] $$
$$ \left[\frac\pi2;\ \frac{5\pi}{4}\right) $$	$$ (1;\ 3) $$
	\begin{gather*} 1\ \text{рад}=\frac{180^{\circ}}{\pi}\approx 57,3^{\circ}\\ 3\ \text{рад}=\frac{180^{\circ}}{\pi}\cdot 3\approx 171,9^{\circ} \end{gather*}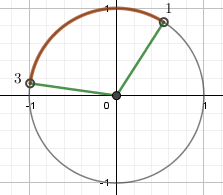